初中数学人教版（2024）九年级上册24.1.1 圆同步测试题

这是一份初中数学人教版（2024）九年级上册24.1.1 圆同步测试题，共8页。试卷主要包含了下列说法正确的是等内容，欢迎下载使用。
单项选择题（本题共12小题，每小题3分，共36分。在每小题给出的四个选项中，只有一项是符合题目要求的。）
1．如图，AB是⊙O直径，BC与⊙O相切于点B，OC与⊙O相交于点D，连结AD，若∠A=24°，则∠C的度数为（ ）
A．24°B．42°C．48°D．52°
2．下列说法正确的是（ ）
A．三个点可以确定一个圆B．半圆（或直径）所对的圆周角是直角
C．相等的圆心角所对的弧相等D．长度相等的弧是等弧
3．已知点P与⊙O在同一平面内，⊙O的半径为6，若PO=8，则点P与⊙O的位置关系是（ ）
A．点P在圆内B．点P在圆上C．点P在圆外D．点P在圆上或圆外
4．如图，在△ABC中，分别以点A和点C为圆心，大于12AC的长为半径作弧（弧所在圆的半径都相等），两弧相交于M，N两点，直线MN分别与边BC,AC相交于点D，E，连接AD．若BD=DC,AE=4,AD=5，则AB的长为（ ）

A．9B．8C．7D．6
5．如图，AB为⊙O的直径，直线CD与⊙O相切于点C，连接AC，若∠ACD=50°，则∠BAC的度数为（ ）

A．30°B．40°C．50°D．60°
6．如图，点A，B，C在⊙O上，若∠C=55°，则∠AOB的度数为（ ）

A．95°B．100°C．105°D．110°
7．如图，△ABC内接于⊙O，CD是⊙O的直径，∠ACD=40°，则∠B=（ ）
A．70°B．60°C．50°D．40°
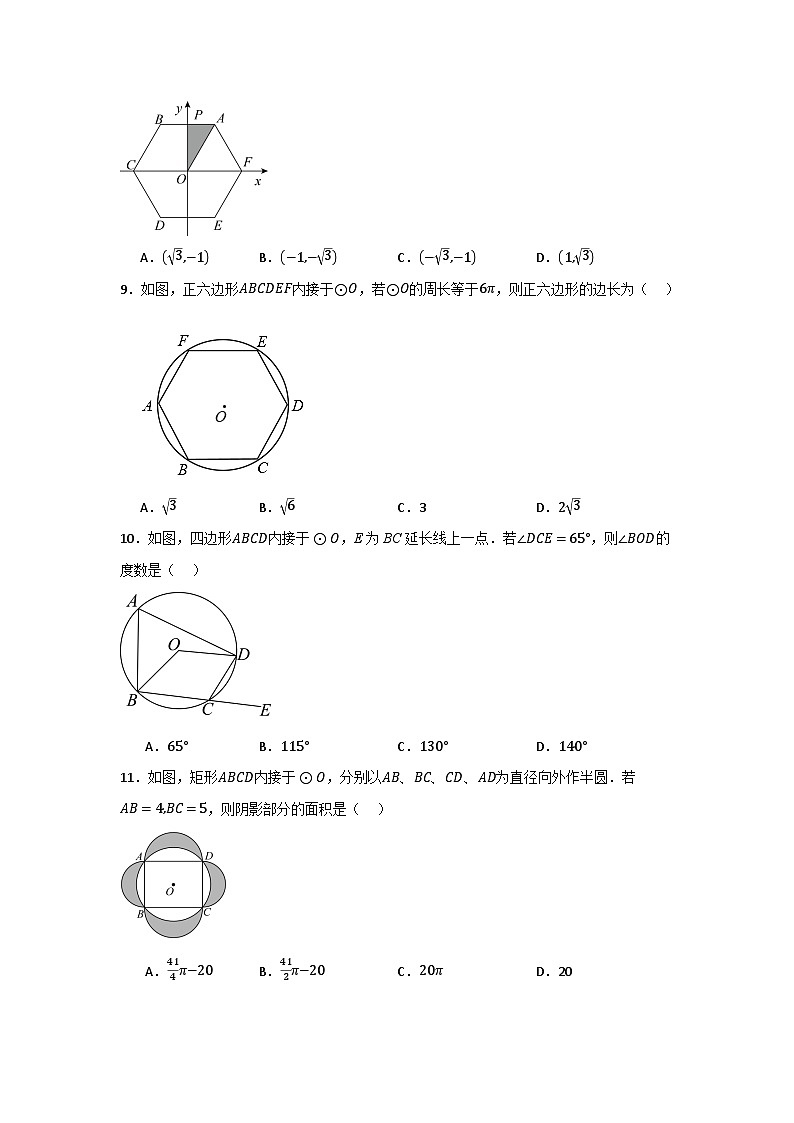
8．如图，在平面直角坐标系中，边长为2的正六边形ABCDEF的中心与原点O重合，AB∥x轴，交y轴于点P．将△OAP绕点O顺时针旋转，每次旋转90°，则第2022次旋转结束时，点A的坐标为（ ）
A．3,−1B．−1,−3C．−3,−1D．1,3
9．如图，正六边形ABCDEF内接于⊙O，若⊙O的周长等于6π，则正六边形的边长为（ ）
A．3B．6C．3D．23
10．如图，四边形ABCD内接于⊙O，E为BC延长线上一点．若∠DCE=65°，则∠BOD的度数是（ ）

A．65°B．115°C．130°D．140°
11．如图，矩形ABCD内接于⊙O，分别以AB、BC、CD、AD为直径向外作半圆．若AB=4,BC=5，则阴影部分的面积是（ ）

A．414π−20B．412π−20C．20πD．20
12．如图，在平面直角坐标系xOy中，直线y=−x−2与x轴、y轴分别交于A、B两点，C、D是半径为1的⊙O上两动点，且CD=2，P为弦CD的中点．当C、D两点在圆上运动时，△PAB面积的最大值是（ ）

A．8B．6C．4D．3
填空题（本题共6小题，每小题2分，共12分．）
13．如图，在⊙O中，AB为直径，C为圆上一点，∠BAC的角平分线与⊙O交于点D，若∠ADC=20°，则∠BAD= °．

14．如图，点A，B，C在半径为2的⊙O上，∠ACB=60°，OD⊥AB，垂足为E，交⊙O于点D，连接OA，则OE的长度为 ．
15．如图，AB是⊙O的直径，点D，M分别是弦AC，弧AC的中点，AC=12,BC=5，则MD的长是 ．

16．如图，圆锥形烟囱帽的底面半径为30cm，母线长为50cm，则烟囱帽的侧面积为 cm2．（结果保留π）

17．一块圆形玻璃镜面碎成了几块，其中一块如图所示，测得弦AB长20厘米，弓形高CD为2厘米，则镜面半径为 厘米．
18．如图，在矩形ABCD中，AB=8，AD=4，点E是矩形ABCD内部一动点，且∠BEC=90°，点P是AB边上一动点，连接PD,PE，则PD+PE的最小值为 ．
三、解答题（本题共8小题，共72分，解答应写出文字说明、证明过程或演算步骤．）
19．（8分）如图，AB为⊙O的直径，如果圆上的点D恰使∠ADC=∠B，求证：直线CD与⊙O相切．

20．（8分）如图，已知在Rt△ABC中，∠C=90°，D是AB边上一点，以BD为直径的半圆O与边AC相切，切点为E，过点O作OF⊥BC，垂足为F．
(1)求证：OF=EC；
(2)若∠A=30°，BD=2，求AD的长．
21．（8分）已知：如图，PA、PB是⊙O的切线，切点分别是A、B，Q为AB上一点，过Q点作⊙O的切线，交PA、PB于E、F点，已知PA=12cm，求△PEF的周长．
22．（8分）如图，AB为⊙O的直径，过圆上一点D作⊙O的切线CD交BA的延长线与点C，过点O作OE//AD交CD于点E，连接BE．
(1)直线BE与⊙O相切吗？并说明理由；
(2)若CA=2，CD=4，求DE的长．
23．（10分）如图，以线段AB为直径作⊙O，交射线AC于点C，AD平分∠CAB交⊙O于点D，过点D作直线DE⊥AC于点E，交AB的延长线于点F．连接BD并延长交AC于点M．
(1)求证：直线DE是⊙O的切线；
(2)求证：AB=AM；
(3)若ME=1，∠F=30°，求BF的长．
24．（10分）石拱桥是我国古代人民勤劳和智慧的结晶（如图1），隋代建造的赵州桥距今约有1400年历史，是我国古代石拱桥的代表．如图2是根据某石拱桥的实物图画出的几何图形，桥的主桥拱是圆弧形，表示为AB．桥的跨度（弧所对的弦长）AB=26m，设AB所在圆的圆心为O，半径OC⊥AB，垂足为D．拱高（弧的中点到弦的距离）CD=5m．连接OB．
(1)直接判断AD与BD的数量关系；
(2)求这座石拱桥主桥拱的半径（精确到1m）．
25．（10分）（1）课本再现：在⊙O中，∠AOB是AB所对的圆心角，∠C是AB所对的圆周角，我们在数学课上探索两者之间的关系时，要根据圆心O与∠C的位置关系进行分类．图1是其中一种情况，请你在图2和图3中画出其它两种情况的图形，并从三种位置关系中任选一种情况证明∠C=12∠AOB；
（2）知识应用：如图4，若⊙O的半径为2，PA,PB分别与⊙O相切于点A，B，∠C=60°，求PA的长．
26．（10分）某种冰激凌的外包装可以视为圆锥，它的底面圆直径ED与母线AD长之比为1:2．制作这种外包装需要用如图所示的等腰三角形材料，其中AB=AC，AD⊥BC．将扇形AEF围成圆锥时，AE，AF恰好重合．
（1）求这种加工材料的顶角∠BAC的大小
（2）若圆锥底面圆的直径ED为5cm，求加工材料剩余部分（图中阴影部分）的面积．（结果保留π）