苏科版数学七年级上册期末复习专题5.3 走进图形世界（章节复习+考点讲练）（2份，原卷版+教师版）

这是一份苏科版数学七年级上册期末复习专题5.3 走进图形世界（章节复习+考点讲练）（2份，原卷版+教师版），文件包含苏科版数学七年级上册期末复习专题53走进图形世界章节复习+考点讲练教师版doc、苏科版数学七年级上册期末复习专题53走进图形世界章节复习+考点讲练学生版doc等2份试卷配套教学资源，其中试卷共56页， 欢迎下载使用。

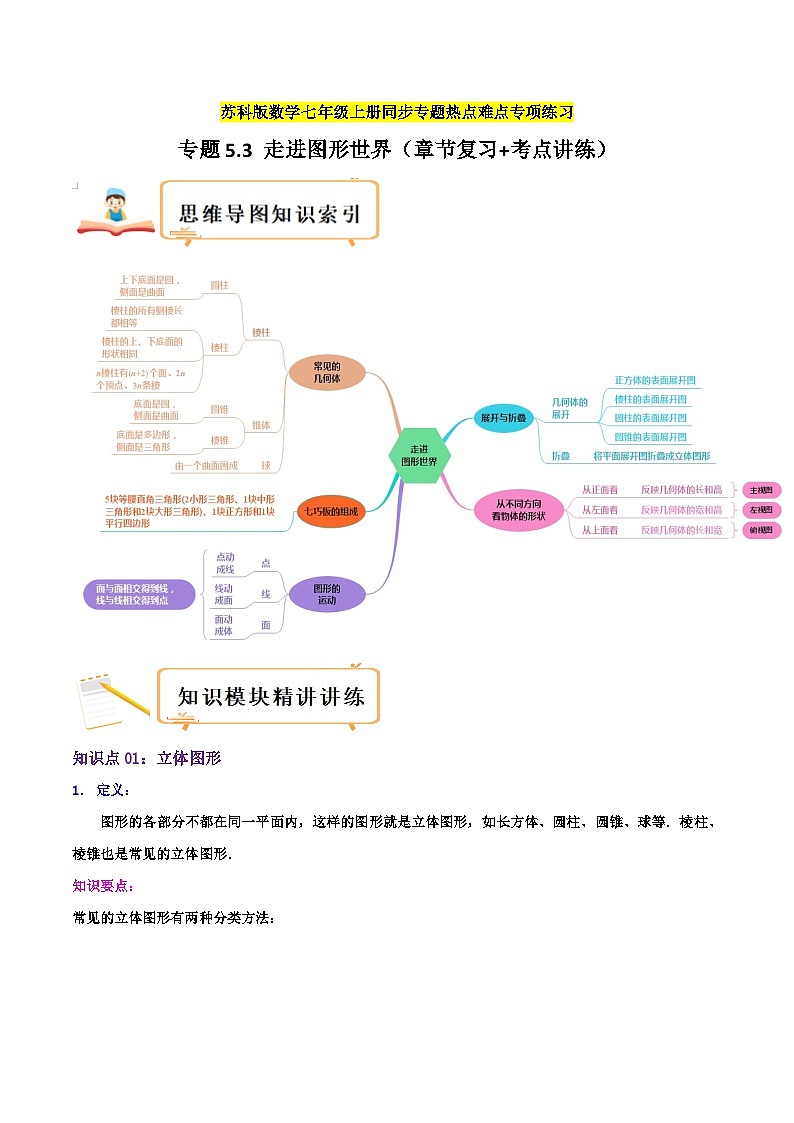
知识点01：立体图形
定义：
图形的各部分不都在同一平面内，这样的图形就是立体图形，如长方体、圆柱、圆锥、球等．棱柱、棱锥也是常见的立体图形．
知识要点：
常见的立体图形有两种分类方法：
棱柱的相关概念：
在棱柱中，相邻两个面的交线叫做棱，相邻两个侧面的交线叫做侧棱． 通常根据底面图形的边数将棱柱分为三棱柱、四棱柱、五棱柱、六棱柱……它们底面图形的形状分别为三角形、四边形、五边形、六边形……（如下图）
知识要点：（1）棱柱所有侧棱长都相等．棱柱的上、下底面的形状相同，侧面的形状都是平行四边形．
（2）长方体、正方体都是四棱柱．
（3）棱柱可分为直棱柱和斜棱柱．直棱柱的侧面是长方形，斜棱柱的侧面是平行四边形．
3．点、线、面、体：
长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体也简称体；包围着体的是面,面有平的面和曲的面两种；面和面相交的地方形成线，线也分为直线和曲线两种；线和线相交的地方形成点．从上面的描述中我们可以看出点、线、面、体之间的关系． 此外，从运动的观点看：点动成线，线动成面，面动成体．
知识点02：展开与折叠
有些立体图形是由一些平面图形围成，将它们的表面适当剪开，可以展开成平面图形，这样的平面图形称为相应立体图形的展开图．
知识要点：(1)不是所有的立体图形都可以展成平面图形．例如，球便不能展成平面图形．
(2)不同的立体图形可展成不同的平面图形；同一个立体图形，沿不同的棱剪开，也可得到不同的平面图．
知识点03：截一个几何体
用一个平面去截一个几何体，截出的面叫做截面．截面的形状可能是三角形、四边形、五边形、六边形或圆等等．
知识点04：从三个方向看物体的形状
一般是从以下三个方向：(1)从正面看；(2)从左面看；(3)从上面看．（如下图）
【典型例题】（2023•青龙县模拟）如图所示，陀螺是由下面哪两个几何体组合而成的（ ）
A．长方体和圆锥B．长方形和三角形
C．圆和三角形D．圆柱和圆锥
【思路点拨】根据立体图形的概念和定义对图进行分析知：该图上部分是圆柱，下部分是圆锥．
【规范解答】解：由组成几何体的特征知，上面是圆柱，下面是圆锥．
故选：D．
【考点再现】本题考查的圆柱和圆锥的定义，关键点在于理解圆柱和圆锥的特征．
【变式训练1-1】（2021秋•高新区期末）如图，将一张正方形纸片的4个角剪去4个大小一样的小正方形，然后折起来就可以制成一个无盖的长方体纸盒，设这个正方形纸片的边长为a，这个无盖的长方体盒子高为h．
（1）若a＝18cm，h＝4cm，则这个无盖长方体盒子的底面面积为 100 cm2；
（2）用含a和h的代数式表示这个无盖长方体盒子的容积V＝ h（a﹣2h）2 cm3；
（3）若a＝18cm，试探究：当h越大，无盖长方体盒子的容积V就越大吗？请举例说明；当h是正整数时，这个无盖长方体盒子的最大容积是 432 cm3．
【思路点拨】（1）根据题目的已知可得，无盖长方体盒子的底面是一个边长为（18﹣2×4）的正方形，然后进行计算即可；
（2）根据长方体的体积公式进行计算即可；
（3）利用（2）的结论进行计算即可解答．
【规范解答】解：由题意可得：
（18﹣2×4）×（18﹣2×4）
＝10×10
＝100（平方厘米），
∴这个无盖长方体盒子的底面面积为100cm2，
故答案为：100；
（2）由题意可得：
这个无盖长方体盒子的容积V＝h（a﹣2h）2cm3，
故答案为h（a﹣2h）2；
（3）若a＝18cm，当h越大，无盖长方体盒子的容积V不一定就越大，
当h＝3时，这个无盖长方体盒子的最大容积是：
V＝3×（18﹣2×3）＝432（立方厘米），
故答案为：当h越大，无盖长方体盒子的容积V不一定就越大，432．
【考点再现】本题考查了认识立体图形，列代数式，代数式求值，熟练掌握长方体的体积公式是解题的关键．
【变式训练1-2】（2023•京口区校级一模）一只小蚂蚁从如图所示的正方体的顶点A沿着棱爬向有蜜糖的点B，它只能经过三条棱，请你数一数，小蚂蚁有 6 种爬行路线．
【思路点拨】根据正方体的特点，依次找到由顶点A沿着棱爬向B，只能经过三条棱的路线即可．
【规范解答】解：如图所示：
走法有：①A﹣C﹣D﹣B；②A﹣C﹣H﹣B；③A﹣E﹣F﹣B；④A﹣E﹣D﹣B；⑤A﹣G﹣F﹣B；⑥A﹣G﹣H﹣B．
共有6种走法．
故答案为：6．
【考点再现】此题主要考查了立体图形的认识，通过正方体考查了路线问题，注意按顺序依次寻找，不要遗漏和重复．
【变式训练1-3】（2021秋•梁溪区校级期中）如图，把一张长方形纸板裁去两个边长为3cm的小正方形和两个全等的小长方形，再把剩余部分（阴影部分）四周折起，恰好做成一个有底有盖的长方体纸盒，纸盒底面长方形的长为3kcm，宽为2kcm，则：
（1）裁去的每个小长方形面积为 （6k+9） cm2．（用k的代数式表示）
（2）若长方体纸盒的表面积是底面积的正整数倍，则正整数k的值为 1或5 ．
【思路点拨】（1）求出小长方形的长与宽，可得结论．
（2）由长方体纸盒的表面积是底面积的正整数倍，推出侧面4个长方形的面积和是底面积的整数倍，延长构建关系式，可得结论．
【规范解答】解：（1）由题意，小长方形的长为（3+2k ）cm，宽为3cm，
∴裁去的每个小长方形面积为（6k+9）（cm2），
故答案为：（6k+9）；
（2）由题意得：
12k+18k＝n•6k2（n为正整数），
可得nk＝5，
∴n＝1，k＝5或n＝5，k＝1，
∴k＝1或5，
故答案为：1或5．
【考点再现】本题主要考查了列代数式，认识立体图形等知识，解题的关键是学会利用参数解决问题，属于中考常考题型．
【典型例题】（2018秋•吴中区期末）圆柱是由长方形绕着它的一边所在直线旋转一周所得到的，那么下列四个选项绕直线旋转一周可以得到如图立体图形的是（ ）
A．B．C．D．
【思路点拨】如图本题是一个平面图形围绕一条边为中心对称轴旋转一周根据面动成体的原理即可解．
【规范解答】解：由长方形绕着它的一边所在直线旋转一周可得到圆柱体，如图立体图形是两个圆柱的组合体，
则需要两个一边对齐的长方形，绕对齐边所在直线旋转一周即可得到，
故选：A．
【考点再现】本题考查面动成体，需注意可把较复杂的体分解来进行分析．
【变式训练2-1】（2022秋•滨海县月考）如图，下面的几何体是由图 ② （填写序号）的平面图形绕直线l旋转一周得到的．
【思路点拨】根据面动成体，所得图形是两个圆锥体的复合体确定答案即可．
【规范解答】解：由图可知，只有图②绕直线l旋转一周得到如图所示立体图形．
故答案为：②．
【考点再现】本题考查了点、线、面、体，熟悉常见图形的旋转得到立体图形是解题的关键．
【变式训练2-2】（2022秋•常州期末）如图，长方形的相邻两边的长分别为x、y，将它分别绕相邻两边旋转一周．
（1）两次旋转所形成的几何体都是 圆柱 ；
（2）若x+y＝a（a是常数），分别记绕长度为x、y的边旋转一周的几何体的体积为Vx、Vy，其中x、Vx、Vy的部分取值如表所示：
①通过表格中的数据计算：a＝ 10 ，m＝ 128π ，n＝ 144π ；
②当x逐渐增大时，Vy的变化情况： 先增大，后减小 ；
③当x变化时，请直接写出Vx与Vy的大小关系．
【思路点拨】（1）根据圆柱的定义可知，旋转所得的几何体是圆柱；
（2）圆柱的体积＝底面积×高，解答即可；
【规范解答】解（1）根据圆柱的定义可知，旋转所得的几何体是圆柱．
故答案为：圆柱；
（2）圆柱的体积＝底面积×高，
①当x＝4时，Vy＝πx2y＝96π，解得y＝6，此时x+y＝10，所以a＝10；
当x＝2时，y＝10﹣2＝8，Vx＝πy2x＝π×8×8×2＝128π＝m；
当x＝6时，y＝10﹣6＝4，Vy＝πx2y＝π×6×6×4＝144π＝n；
故答案为：10，128π，144π；
②V＝πx2y＝πx2（10﹣x），
当x逐渐增大时，V的变化为：先增大，后减小．
故答案为：先增大，后减小；
③Vy＝πx2у＝πх2（10﹣x），Vx＝πу2х＝π （10﹣x）2x，
当Vy≥VX时，x2（10﹣x）≥π（10﹣x）2x，解得x≥5，
当Vy＜Vx时，πx（10﹣x）＜π（10﹣x）2x，解得0＜x＜5，
综上所述，x≥5时，Vy≥VX，；0＜x＜5时，Vy＜Vx．
【考点再现】本题考查了点、线、面、体，掌握圆柱的体积＝底面积×高是解题的关键．
【典型例题】（2020秋•无锡期末）如图是一个长方体储水箱和一个长方体水池的侧面示意图（厚度忽略不计），储水箱中水深12dm，把一高度为14dm的长方体石柱放置于水池中央后水池中水深2dm．现将储水箱中的水匀速注入水池．注水4min时水池水面与石柱上底面持平；继续注水2min后，储水箱中的水全部注入水池，此时水池中水深19dm．根据上述信息，解答下列问题：
（1）注水多长时间时，储水箱和水池中的水的深度相同？
（2）若水池底面积为42dm2，求石柱的底面积；
（3）若石柱的体积为168dm3，请直接写出注水前储水箱中水的体积．
【思路点拨】（1）先根据题意求出储水箱出水速度和水池注水速度，再设tmin时深度相同，列方程求解即可；
（2）设石柱底面积S＝adm2，依据储水箱出水速度相同列方程求解；
（3）先求得石柱的底面积，再通过列方程求出水池底面积，最后列方程求注水前储水箱中水的体积．
【规范解答】（1）储水箱出水速度：12÷6＝2（dm/min），水池注水速度：（14﹣2）÷4＝3（dm/min），
设tmin时深度相同，则：
12﹣2t＝2+3t，
解得：t＝2，
答：注水2min时，储水箱和水池中的水的深度相同．
（2）设石柱底面积S＝adm2，
则：（14﹣2）×（42﹣a）＝2×（19﹣14）×42，
解得：a＝7，
故石柱的底面积为7dm2．
（3）∵石柱的体积为168dm3，
∴石柱的底面积为：168÷14＝12（dm2），
依题意，得：
（19﹣14）•S水池÷（6﹣4）＝（14﹣2）•（S水池﹣12）÷4，
解得：S水池＝72（dm2），
12÷6×4×S储水箱＝（72﹣12）×（14﹣2），
解得：S储水箱＝90（dm2），
∴注水前储水箱中水的体积V＝S储水箱•h＝90×12＝1080（dm3）．
【考点再现】本题考查了柱体的底面积、体积计算公式，一元一次方程的应用等，题目比较简单，解题时一定要认真审题，理解题意，找准等量关系，建立方程求解．
【变式训练3-1】（2022秋•兴化市校级期末）如图，由27个相同的小正方体拼成一个大正方体，从中取出一块小正方体，剩下的图形表面积最大的取法为（ ）
A．取走①号B．取走②号C．取走③号D．取走④号
【思路点拨】弄清取出小正方体后，其剩下的图形的表面积与原正方体的面表积的关系即可．
【规范解答】解：取走①号或③号剩下的图形表面积不变，取走②号剩下的图形表面积增大两个小正方体的面，取走④号剩下的图形表面积增大4个小正方体的面，
故选：D．
【考点再现】本题主要考查几何体的表面积，关键是挖去的正方体中相对的面的面积都相等．
【变式训练3-2】（2019秋•扬州期末）由5个棱长为1的小正方体组成的几何体如图放置，一面着地，两面靠墙，如果要将露出来的部分涂色，则涂色部分的面积为 11 ．
【思路点拨】由涂色部分面积是从上、前、右三个方向所涂面积相加，据此可得．
【规范解答】解：由图可知涂色部分是从上、前、右三个方向所涂面积相加，即涂色部分面积为4+4+3＝11，
故答案为：11．
【考点再现】本题主要考查几何体的表面积，解题的关键是掌握涂色部分是从上、前、右三个方向所涂面积相加的结果．
【变式训练3-3】（2019秋•盱眙县期末）如图，在平整的地面上，有若干个完全相同的棱长为10cm的小正方体堆成一个几何体．
（1）这个几何体由 10 个小正方体组成．
（2）如果在这个几何体的表面喷上黄色的漆，则在所有的小正方体中，有 1 个正方体只有一个面是黄色，有 2 个正方体只有两个面是黄色，有 3 个正方体只有三个面是黄色．
（3）这个几何体喷漆的面积为 3200 cm2．
【思路点拨】（1）根据几何体的形状，可得左列三排，第一排一层，第二排两层，后排三层，中间列两排，每排一层，右列一排，共一层，可得答案；
（2）根据几何体的形状，可得小正方体露出表面的个数；
（3）根据露出的小正方体的面数，可得几何体的表面积．
【规范解答】解：（1）这个几何体由 10个小正方体组成．
（2）如果在这个几何体的表面喷上黄色的漆，则在所有的小正方体中，有 1个正方体只有一个面是黄色，有 2个正方体只有两个面是黄色，有 3个正方体只有三个面是黄色．
（3）露出表面的面一共有32个，则这个几何体喷漆的面积为3200cm2，
故答案为：10；1，2，3；3200．
【考点再现】本题考查了几何体的表面积，小正方体露出面的面积和，露出4个面的有两个正方形，露出5个面的有两个正方形．
【典型例题】（2022秋•张家港市期中）如图所示，连接边长为1的正方形各边的中点，连接正方形的对角线，则图中共有三角形（ ）

A．16个B．32个C．22个D．44个
【思路点拨】先计算最小的三角形的个数，然后计算两个三角形组成的三角形的个数，再计算四个三角形组成的三角形的个数，再计算八个三角形组成的三角形的个数，从而可得出答案．
【规范解答】解：根据图形得：最小的三角形有4×4＝16个；
两个三角形组成的三角形有4×4＝16；
四个三角形组成的三角形有：8个；
八个三角形组成的三角形有：4个．
∴共有16+16+8+4＝44个．
故选：D．
【考点再现】本题考查图形数量的确定，难度不大，按一定的顺序，按一定的方向查找．
【变式训练4-1】（2013秋•泰兴市校级期中）定义：两个直角三角形，若一个三角形的两条直角边分别与另一个三角形的两条直角边相等，我们就说这两个直角三角形是“同胞直角三角形”．如图，在边长为10的正方形中有两个直角三角形，当直角三角形①和直角三角形②是同胞直角三角形时，a的值是 5或6 ．
【思路点拨】根据“同胞直角三角形”的定义结合图形可直接得到答案．
【规范解答】解：由“同胞直角三角形”的定义可得：当a＝6时，b＝4，c＝4符合题意；
当a＝5时，b＝5，c＝6，符合题意，
故a＝5或6，
故答案为：5或6．
【考点再现】此题主要考查了认识平面图形，关键是正确理解题意．
1【变式训练4-2】（2022秋•崇川区校级月考）如图，半径为1个单位长度的圆片上有一点Q与数轴上的原点重合（提示：圆的周长C＝2πr，π取3.14）

（1）把圆片沿数轴向左滚动1周，点Q到达数轴上点A的位置，点A表示的数是 ﹣6.28 ；
（2）圆片在数轴上向右滚动的周数记为正数，圆片在数轴上向左滚动的周数记为负数，依次运动情况记录如下：2，﹣1，﹣5，4，3，﹣2．
①第几次滚动后，Q点距离原点最近？第几次滚动后，Q点距离原点最远？
②当圆片结束运动时，Q点运动的路程共有多少？此时点Q所表示的数是多少？
【思路点拨】（1）利用圆的半径以及滚动周数即可，得出滚动距离；
（2）①利用滚动的方向以及滚动的周数即可，得出Q点移动距离变化；
②利用绝对值得性质以及有理数的加减运算得出移动距离和Q表示的数即可．
【规范解答】解：（1）∵2πr＝2×3.14×1＝6.28，
∴点A表示的数是﹣6.28，
故答案为：﹣6.28；
（2）①∵+2﹣1﹣5+4＝0，
∴第4次滚动后，Q点距离原点最近；
∵（+2）+（﹣1）+（﹣5）＝﹣4，
∴第3次滚动后，Q点距离原点最远；
②∵|+2|+|﹣1|+|﹣5|+|+4|+|+3|+|﹣2|＝17，
∴17×2π×1＝106.76，
∴当圆片结束运动时，Q点运动的路程共有106.76，
∵2﹣1﹣5+4+3﹣2＝1，
∴1×2π×1≈6.28，
∴此时点Q所表示的数是6.28．
【考点再现】此题主要考查了数轴的应用以及绝对值得性质和圆的周长公式应用，利用数轴得出对应数是解题关键．
【典型例题】（2021秋•兴化市月考）如图所示是一个几何体的表面展开图．
（1）该几何体的名称是 圆柱 ，其底面半径为 1 ．
（2）根据图中所给信息，求该几何体的侧面积和体积．（结果保留π）
【思路点拨】（1）依据展开图中有长方形和两个全等的圆，即可得出结论；
（2）依据圆柱的侧面积和体积计算公式，即可得到该几何体的侧面积和体积．
【规范解答】解：（1）该几何体的名称是圆柱，其底面半径为1，
故答案为：圆柱；1；
（2）该几何体的侧面积为：2π×1×3＝6π；
该几何体的体积＝π×12×3＝3π．
【考点再现】本题主要考查了几何体的展开图，从实物出发，结合具体的问题，辨析几何体的展开图，通过结合立体图形与平面图形的转化，建立空间观念，是解决此类问题的关键．
【变式训练5-1】（2022秋•滨海县月考）如图是正方体的一种展开图，表面上的语句为北京2022年冬奥会和冬残奥会的主题口号“一起向未来!”，那么在正方体的表面与“!”相对的汉字是 一 ．
【思路点拨】由平面图形的折叠及立体图形的表面展开图的特点解题．
【规范解答】解：对于正方体的平面展开图中相对的面一定相隔一个小正方形，由图形可知，与“!”字相对的字是“一”．
故答案为：一．
【考点再现】本题考查生活中的立体图形与平面图形，注意正方体的空间图形，从相对面入手，分析及解答问题．
【变式训练5-2】（2023•盐都区一模）如图是一个几何体的表面展开图，这个几何体是（ ）
A．B．
C．D．
【思路点拨】根据几何体的表面展开图可以判断这个几何体是三棱柱．
【规范解答】解：根据几何体的展开图可知：
这个几何体是：．
故选：C．
【考点再现】本题考查了几何体的展开图，多数立体图形是由平面图形围成的．沿着棱剪开就得到平面图形，这样的平面图形就是相应立体图形的展开图．同一个立体图形按不同的方式展开，得到的平面展开图是不一样的，同时也可看出，立体图形的展开图是平面图形．
【变式训练5-3】（2022秋•姑苏区校级期末）如图是一个几何体的侧面展开图，则该几何体是（ ）
A．三棱柱B．三棱锥C．五棱柱D．五棱锥
【思路点拨】根据几何体的侧面展开图可知该几何体为五棱锥，所以它的底面是五边形．
【规范解答】解：由题意可知，该几何体为五棱锥，所以它的底面是五边形．
故选：D．
【考点再现】本题主要考查了几何体的展开图，熟练掌握棱锥的展开图是解答本题的关键．
【变式训练5-4】．（2017秋•连云区期末）小明在学习了《展开与折叠》这一课后，明白了很多几何体都能展开成平面图形．于是他在家用剪刀展开了一个长方体纸盒，可是一不小心多剪了一条棱，把纸盒剪成了两部分，即图中的①和②．根据你所学的知识，回答下列问题：
（1）小明总共剪开了 8 条棱．
（2）现在小明想将剪断的②重新粘贴到①上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，你认为他应该将剪断的纸条粘贴到①中的什么位置？请你帮助小明在①上补全．
（3）小明说：他所剪的所有棱中，最长的一条棱是最短的一条棱的5倍．现在已知这个长方体纸盒的底面是一个正方形，并且这个长方体纸盒所有棱长的和是880cm，求这个长方体纸盒的体积．
【思路点拨】（1）根据平面图形得出剪开棱的条数，
（2）根据长方体的展开图的情况可知有四种情况，
（3）设最短的棱长高为acm，则长与宽相等为5acm，根据棱长的和是880cm，列出方程可求出长宽高，即可求出长方体纸盒的体积．
【规范解答】解（1）小明共剪了8条棱，
故答案为：8．
（2）如图，四种情况．
（3）∵长方体纸盒的底面是一个正方形，
∴设最短的棱长高为acm，则长与宽相等为5acm，
∵长方体纸盒所有棱长的和是880cm，
∴4（a+5a+5a）＝880，解得a＝20cm，
∴这个长方体纸盒的体积为：20×100×100＝200000立方厘米．
【考点再现】本题主要考查了几何展开图，结合具体的问题，辨析几何体的展开图，通过结合立体图形与平面图形的转化，建立空间观念，是解决此类问题的关键．
【典型例题】（2016秋•泰兴市期末）将如图所示的图形剪去一个小正方形，使余下的部分恰好能折成一个正方体，下列编号为1、2、3、6的小正方形中不能剪去的是 3 （填编号）．
【思路点拨】根据正方体的展开图中每个面都有唯一的一个对面进行判断，可得答案．
【规范解答】解：由图可得，3的唯一对面是5，而4的对面是2或6，7的对面是1或2，
所以将如图所示的图形剪去一个小正方形，使余下的部分恰好能折成一个正方体，编号为1、2、3、6的小正方形中不能剪去的是3，
故答案为：3．
【考点再现】本题考查了展开图折叠成几何体，利用正方体的展开图中每个面都有唯一的一个对面是解题关键．
【变式训练6-1】（2022秋•苏州期末）将如图所示的图形剪去一个小正方形，使余下的部分恰好能折成一个正方体，则下列序号中不应剪去的是（ ）
A．3B．2C．6D．1
【思路点拨】正方体有6个面组成，每一个顶点出有3个面，有4个面的地方，必须剪去一个，如果剪去3，1、2、5、6出有4个面，无法折．
【规范解答】解：正方体有6个面组成，每一个顶点出有3个面，
∴1、2、6必须剪去一个，
故选：A．
【考点再现】本题考查的是展开图折叠成几何体，解题的关键是了解正方体的特征．
【变式训练6-2】（2022秋•鼓楼区校级期末）小明用如图所示的纸板折成了一个正方体的盒子，里面装了一瓶墨水，与其他三个空盒子混放在一起，观察四个选项，可知墨水瓶所在的盒子是（ ）
A．B．C．D．
【思路点拨】根据正方体的展开图的特征，折叠后各个面以及顶点之间的关系进行判断即可．
【规范解答】解：如图，当将其进行折叠后，点A与点B重合，点C与点D重合，
阴影三角形的两个直角顶点重合在一起，并且与含有“〇”面的四个顶点重合的点为C、D、E、F、G，
点A、点B不能与含有“〇”面的顶点重合，
因此，只有B是正确的，
故选：B．
【考点再现】本题考查正方体的展开与折叠，理解和掌握展开、折叠前后的面、顶点之间的关系是正确判断的关键．
【变式训练6-3】（2022秋•太仓市期末）某数学兴趣小组开展了“制作一个尽可能大的无盖长方体纸盒”的实践活动，他们利用边长为a厘米的正方形纸板制作出一个无盖的长方体纸盒（纸板厚度及接缝处忽略不计）．具体方法如下：如图，先在纸板四角剪去四个同样大小的小正方形，再沿虚线折合起来，这样可制作一个无盖的长方体纸盒．设底面边长为x（x＜a）厘米．
（1）这个纸盒的底面积是 x2 平方厘米，高是 厘米（用含a，x的代数式表示）．
（2）x的部分取值及相应的纸盒容积如表所示：
①请通过表格中的数据，分别计算m，n，p的值；（请详细写出求解过程）
②请在该纸板上调整剪去小正方形的尺寸，重新制作一个无盖长方体纸盒，使得新纸盒的容积大于表格中的四个容积值，则x＝ 7 厘米．（写出一个符合题意的结果即可）
【思路点拨】（1）根据正方形的面积公式求解；
（2）①先根据x＝4，V＝48求出a的值，再计算m、n、p的值；
③根据①表中的数据的增减性求解．
【规范解答】解：（1）这个纸盒的底面积是x2平方厘米，高是厘米，
故答案为：x2，；
（1）①∵16×＝48，
∴a＝10，
∴m＝4×4＝16，
n＝36×2＝72，
p＝64×1＝64；
②当x＝7时，V＝49×1.5＝73.5，
故答案为：7．
【考点再现】本题考查了展开图折叠成几何体，掌握有理数的运算是解题的关键．
【典型例题】（2021秋•淮阴区期末）有一个正方体骰子，放在桌面上，将骰子沿如图所示的顺时针方向滚动，每滚动90°算一次，则滚动第2022次后，骰子朝下一面的点数是（ ）
A．5B．3C．4D．2
【思路点拨】先找出正方体相对的面，然后从数字找规律即可解答．
【规范解答】解：由图可知：
3和4相对，2和5相对，1和6相对，
将骰子沿如图所示的顺时针方向滚动，每滚动90°算一次，骰子朝下一面的点数依次为2，3，5，4，且依次循环，
∵2022÷4＝，
∴滚动第2022次后，骰子朝下一面的点数是：3，
故选：B．
【考点再现】本题考查了正方体相对两个面上的文字，先找出正方体相对的面，然后从数字找规律是解题的关键．
【变式训练7-1】（2022秋•亭湖区期末）一个正方体的表面展开图如图所示，六个面上各有一字，连起来的意思是“沉着冷静应考”，把它折成正方体后，与“静”相对的字是 着 ．
​
【思路点拨】根据正方体表面展开图的特征进行判断即可．
【规范解答】解：由正方体表面展开图的“相间、Z端是对面”可知，
“静”与“着”是对面，
故答案为：着．
【考点再现】本题考查正方体相对两个面上的文字，掌握正方体表面展开图的特征是正确判断的关键．
【变式训练7-2】（2022秋•兴化市期末）如图1，边长为acm的正方形硬纸板的4个角上剪去相同的小正方形，这样可制作一个无盖的长方体纸盒，设底面边长为xcm．
（1）这个纸盒的底面积是 x2 cm2，高是 （用含a、x的代数式表示）．
（2）若将正方形硬纸板按图2方式裁剪，亦可制作一个无盖的长方体纸盒．
①若为该纸盒制作一长方形盖子，则该长方形的两边长分别是 y cm， a﹣2y cm（用含a、y的代数式表示）；
②已知A，B，C，D四个面上分别标有整式2（m+2），m，﹣3，6，且该纸盒的相对两个面上的整式的和相等，求m的值．
【思路点拨】（1）根据长方形的面积公式结合进行计算即可；
（2）①结合图形进行计算即可解答，
②结合图形可知A与C相对，B与D相对，然后进行即可解答．
【规范解答】解：（1）这个纸盒的底面积是x2cm2，高是
cm，
故答案为：x2，；
（2）①若为该纸盒制作一个长方形盖子，则该长方形的两边长分别是ycm，（a﹣2y）cm，
故答案为：y，a﹣2y；
②由图可知：A与C相对，B与D相对，
由题意得：
2（m+2）+（﹣3）＝m+6，
2m+4﹣3＝m+6，
m＝5，
∴m的值为5．
【考点再现】本题考查了正方体相对两个面上的文字，列代数式，整式的加减，解一元一次方程，准确熟练地进行计算是解题的关键．
【变式训练7-3】（2021秋•高港区月考）一个小立方体的六个面分别标有字母A，B，C，D，E，F从三个不同方向看到的情形如图所示．
（1）A对面的字母是 C ，B对面的字母是 D ，E对面的字母是 F ．（请直接填写答案）
（2）若A＝2x﹣1，B＝﹣3x+9，C＝﹣7，D＝1，E＝2x+5，F＝﹣9，且字母E与它对面的字母表示的数互为相反数，求A，B的值．
【思路点拨】（1）观察三个正方体，与A相邻的字母有D、E、B、F，从而确定出A对面的字母是C，与B相邻的字母有C、E、A、F，从而确定与B对面的字母是D，最后确定出E的对面是F；
（2）根据互为相反数的定义列出求出x，然后代入代数式求出A、B的值即可．
【规范解答】解：（1）由图可知，A相邻的字母有D、E、B、F，
所以，A对面的字母是C，
与B相邻的字母有C、E、A、F，
所以B对面的字母是D，
所以E对面的字母是F；
故答案为：C，D，F；
（2）∵字母E与它对面的字母表示的数互为相反数，
∴2x+5+（﹣9）＝0，
解得x＝2，
∴A＝2x﹣1＝4﹣1＝3；
B＝﹣3x+9＝﹣6+9＝3．
【考点再现】本题考查了正方体相对两个面上的文字，根据相邻面的情况确定出相邻的四个字母是确定对面上的字母的关键，也是解题的难点．
【典型例题】（2021秋•苏州期末）用一个平面去截正方体，截面可能是下列图形中的（ ）
①三角形；②四边形；③五边形；④六边形；⑤七边形．
A．①②③④B．①②③⑤C．③④⑤D．②④⑤
【思路点拨】根据正方体的截面形状判断即可．
【规范解答】解：因为：正方体的截面可能是三角形，四边形，五边形，六边形，不可能是七边形，
所以：用一个平面去截正方体，截面可能是下列图形中的三角形，四边形，五边形，六边形，
故选：A．
【考点再现】本题考查了截一个几何体，熟练掌握正方体的截面形状是解题的关键．
【变式训练8-1】（2022秋•江宁区月考）正方体切去一个块，可得到如图几何体，这个几何体有（ ）条棱．
A．10B．11C．12D．13
【思路点拨】通过观察图形即可得到答案．
【规范解答】解：把正方体截去一个角后得到的几何体有12条棱．
故选：C．
【考点再现】此题主要考查了认识正方体，关键是看正方体切的位置．
【变式训练8-2】（2017秋•广陵区校级月考）如图，有一个立方体，它的表面涂满了红色，在它每个面上切两刀，得到27个小立方体，而且凡是切面都是白色．问：
（1）小立方体中三面红的有几块？两面红的呢？一面红的呢？没有红色的面呢？
（2）如果每面切三刀，情况又怎样呢？
（3）每面切n刀呢？
【思路点拨】（1）三面红色对应8个顶角上的小立方块，8个；两面红色对应6条边每条中间的那2小立方块，12个；一面红色对应6个面每个面中心的那个小立方块，6个；最后各面都没有颜色对应大立方体中心的那个小立方块，1个；进行计算即可；
（2）每面切三刀，可得64个小立方体，三面红色对应8个顶角上的小立方块，8个；两面红色对应6条边每条中间的那4小立方块，24个；一面红色对应6个面每个面中心的那4小立方块，24个；最后各面都没有颜色对应大立方体中心的那个小立方块，23＝8个；
（3）每面切n刀，可得（n+1）3个小立方体，三面红色对应8个顶角上的小立方块，8个；两面红色对应6条边每条中间的那（2n﹣2）小立方块，6（2n﹣2）个；一面红色对应6个面每个面中心的那（n﹣1）2小立方块，6（n﹣1）2个；最后各面都没有颜色对应大立方体中心的那个小立方块，（n﹣1）3个．
【规范解答】解：（1）小立方体中三面红的有8块，两面红的12块，一面红的6块，没有红色的1块．
（2）如果每面切三刀，小立方体中三面红的有8块，两面红的24块，一面红的24块，没有红色的8块．
（3）每面切n刀，小立方体中三面红的有8块，两面红的6（2n﹣2）块，一面红的6（n﹣1）2块，没有红色的（n﹣1）3块．
【考点再现】本题主要考查了截一个几何体，应结合立体图形的有关知识进行分析，并根据生活实际进行解答．
【变式训练8-3】（2022秋•宁德期末）如图是一个三棱柱，用平面从中截去一个三棱柱后，剩下的几何体是 三棱柱或四棱柱 （写出所有可能的结果）．
【思路点拨】此题是截去一个三棱柱，切法很关键，我们可以选择最简单、最直观的做法，从三棱柱正中切下一刀，那么切下一个三棱柱，还剩一个三棱柱．从三棱柱竖直方向切下一刀，那么切下一个三棱柱，还剩一个四棱柱．依此即可求解
【规范解答】解：由分析可知，一个三棱柱，用平面从中截去一个三棱柱后，剩下的几何体是三棱柱或四棱柱．
故答案为：三棱柱或四棱柱．
【考点再现】本题考查三棱柱的截面，切法很关键，可选择较简单的切法．
【典型例题】（2021秋•无锡期末）下列立体图形中，俯视图是三角形的是（ ）
A．B．C．D．
【思路点拨】俯视图是从物体上面看所得到的图形，据此判断得出物体的俯视图．
【规范解答】解：A、圆锥体的俯视图是圆，故此选项不合题意；
B、三棱柱的俯视图是三角形，故此选项符合题意；
C、球的俯视图是圆，故此选项不合题意；
D、圆柱体的俯视图是圆，故此选项不合题意；
故选：B．
【考点再现】本题考查了几何体的三视图，掌握定义是关键．注意所有的看到的棱都应表现在三视图中．
【变式训练9-1】（2022秋•丹徒区月考）如图所示，水平放置的长方体的底面是长为4cm、宽为2cm的长方形，它的主视图的面积为12cm2，则长方体的体积等于 24 cm3．
【思路点拨】由主视图的面积＝长×高，长方体的体积＝主视图的面积×宽，得出结论．
【规范解答】解：依题意，得长方体的体积＝12×2＝24（cm3）．
故答案为：24．
【考点再现】本题考查了简单几何体的三视图．关键是明确主视图是由长和高组成的．
【变式训练9-2】（2021秋•灌云县校级月考）在如图所示的几何体中，主视图是三角形的是 ③ ．（填序号）
【思路点拨】找到从正面看所得到的图形，得出主视图是三角形的即可．
【规范解答】解：①的主视图是矩形；②的主视图是矩形，③的主视图是等腰三角形．
∴主视图是三角形的是③．
故答案为：③．
【考点再现】本题考查了三视图的知识，主视图是从物体的正面看得到的视图．
【变式训练9-3】（2022秋•姑苏区校级期末）如图是由棱长都为1cm的6块小正方体组成的简单几何体．
（1）请在方格中画出该几何体的三个视图．
（2）如果在这个几何体上再添加一些小正方体，并保持主视图和左视图不变，最多可以再添加 2 块小正方体，
【思路点拨】（1）根据简单组合体三视图的画法画出相应的图形即可；
（2）在俯视图上相应位置备注出相应摆放的数目即可．
【规范解答】解：（1）该几何体的主视图、左视图和俯视图如下：
（2）在备注数字的位置加摆相应数量的小正方体，
所以最多可以添加2个，
故答案为：2．
【考点再现】本题考查简单组合体的三视图，理解视图的意义是正确解答的前提．
【典型例题】（2020秋•射阳县校级月考）由6个相同的小正方体搭成的几何体如图所示，则它的主视图是（ ）
A．B．
C．D．
【思路点拨】根据从正面看得到的图形是主视图，可得答案．
【规范解答】解：从正面看第一层是三个小正方形，第二层左边是一个小正方形，
故选：D．
【考点再现】本题考查了简单组合体的三视图，从正面看得到的图形是主视图．
【变式训练10-1】（2017春•邗江区校级月考）如图所示物体的左视图为（ ）
A．B．C．D．
【思路点拨】根据左视图是从左边看得到的图形，可得答案．
【规范解答】解：从左边看下边是一个大矩形，矩形的左上角是一个小矩形，
故选：A．
【考点再现】本题考查了简单组合体的三视图，从左边看得到的图形是左视图．
【变式训练10-2】（2021秋•泰兴市期末）如图几何体的主视图为（ ）
A．B．C．D．
【思路点拨】根据从正面看得到的图形是主视图，可得答案．
【规范解答】解：从正面看，是一个正方形，且正方形的右上角有一条实线把正方形分成一个三角形和一个直角梯形．
故选：C．
【考点再现】本题考查了简单组合体的三视图，从正面看得到的图形是主视图．
【变式训练10-3】（2017秋•高新区期末）一个几何体的主视图和俯视图如图所示，若这个几何体最多有m个小正方体组成，最少有n个小正方体组成，m+n＝ 16 ．
【思路点拨】这种题需要空间想象能力，可以想象这样的小立方体搭了左中右三排，但最左排可以为4～6个小正方体，依此求出m、n的值，从而求得m+n的值．
【规范解答】解：最少需要7块如图（1），最多需要9块如图（2）
故m＝9，n＝7，则m+n＝16．
【考点再现】本题灵活考查了三种视图之间的关系以及视图和实物之间的关系，同时还考查了对图形的想象力．
【变式训练10-4】（2022•沭阳县开学）如图，在平整的地面上，用多个棱长都为2cm的小正方体堆成一个几何体．
（1）共有 10 个小正方体；
（2）求这个几何体主视图与俯视图的面积；
（3）如果现在你还有一些棱长都为2cm的小正方体，要求保持俯视图和左视图都不变，最多可以再添加 5 个小正方体．
【思路点拨】（1）根据拼图可直接得出答案；
（2）求出主视图、俯视图的面积即可；
（3）结合三视图，在俯视图上的相应位置添加相应数量的正方体，直至最多．
【规范解答】解：（1）根据拼图可知，堆成如图所示的几何体需要10个小正方体，
故答案为：10；
（2）这个组合体的二视图如图所示：
因此主视图的面积为2×2×7＝28（cm2），俯视图的面积为2×2×7＝28（cm2），
（3）在俯视图的相应位置摆放相应数量的小正方体，使其俯视图和左视图都不变，如图所示，
所以最多可以添加5个，
故答案为：5．
【考点再现】本题考查简单组合体的三视图，理解视图的意义，掌握简单三视图的画法是正确解答的关键．
【典型例题】（2022秋•丹徒区期末）如图是某个几何体的三视图，则该几何体的名称是 三棱柱 ．
【思路点拨】由主视图和左视图确定是柱体，锥体还是球体，再由俯视图确定具体形状．
【规范解答】解：根据主视图和左视图为矩形判断出是柱体，根据俯视图是三角形可判断出这个几何体应该是三棱柱．
故答案为：三棱柱．
【考点再现】考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．
【变式训练11-1】．（2021秋•东海县月考）在一张桌子上摆放着一些碟子，从3个方向看到的3种视图如图所示，则这个桌子上的碟子的个数是（ ）
A．12B．13C．14D．15
【思路点拨】从俯视图中可以看出最底层碟子的个数及形状，从主视图和左视图可以看出每一层碟子的个数，从而算出总的个数．
【规范解答】解：易得三摞碟子数第一列从上往下分别为4，5；第二列是3，
则这个桌子上共有4+5+3＝12（个）碟子．
故选：A．
【考点再现】本题考查对三视图的理解应用及空间想象能力．可从主视图和左视图上分清物体的上下和左右的层数，从俯视图上分清物体的左右和前后位置，综合上述分析数出碟子的个数．
【变式训练11-2】（2019秋•崇川区校级期末）如图是从不同角度看“由相同的小正方体组成的几何体”得到的图形，组成整个几何体的小正方体的个数是（ ）
A．7B．6C．5D．4
【思路点拨】主视图、左视图、俯视图是分别从物体正面、左面和上面看，仔细观察图象即可得到图象．
【规范解答】解：根据题中图象可知：该几何体的下层分两排，前面一排有一个小正方体，后面一排有三个小正方体，上面一层有一个小正方体．
故一共有5个小正方体，
故选：C．
【考点再现】本题主要考查了三视图的概念．考查了学生空间想象能力和细心观察事物的能力，属于基础题．
【变式训练11-3】（2022秋•苏州期末）如图，从三个不同方向看同一个几何体得到如下平面图形，则这个几何体的侧面积是 72 cm2．
【思路点拨】利用三视图可得出几何体的形状，再利用已知各棱长得出这个几何体的侧面积．
【规范解答】解：这个几何体是直三棱柱，
4×6×3＝72（cm2）．
故这个几何体的侧面积是72cm2．
故答案为：72．
【考点再现】此题主要考查了由三视图判断几何体的形状，正确得出物体的形状是解题关键．
【变式训练11-4】（2021秋•泗洪县期末）用若干大小相同的小正方体搭一个几何体，使得从正面和从上面看到的这个几何体的形状如图所示完成下列问题：
（1）搭成满足如图所示主视图和俯视图的几何体最多需要 10 个小正方体，请在网格中画出用最多小正方体搭成的几何体的左视图；
（2）搭成满足如图所示主视图和俯视图的几何体最少需要 7 个小正方体，用最少小正方体搭成的几何体共有 6 种不同形状．
（3）用8块小正方体搭成满足如图所示主视图和俯视图的几何体一共有多少种不同形状？
【思路点拨】（1）在俯视图中，写出最多时，小正方体的个数，可得结论；
（2）利用俯视图，结合主视图的特征，解决问题即可；
（3）根据题意判断即可．
【规范解答】解：（1）搭成满足如图所示主视图和俯视图的几何体最多需要：2+2+2+2+2＝10（个），左视图如图所示．
故答案为：10；
（2）搭成满足如图所示主视图和俯视图的几何体最少需要7个小正方体，用最少小正方体搭成的几何体共有6种不同形状．
故答案为：7，6；
（3）用8块小正方体搭成满足如图所示主视图和俯视图的几何体一共有9种不同形状．
【考点再现】本题考查由三视图判断几何体，解题的关键是理解三视图的定义，属于中考常考题型
x
1
2
3
4
5
6
7
8
9
Vx
m
Vy
96π
n
x/厘米
2
4
6
8
纸盒容积V/立方厘米
m
48
n
p
a−x
2