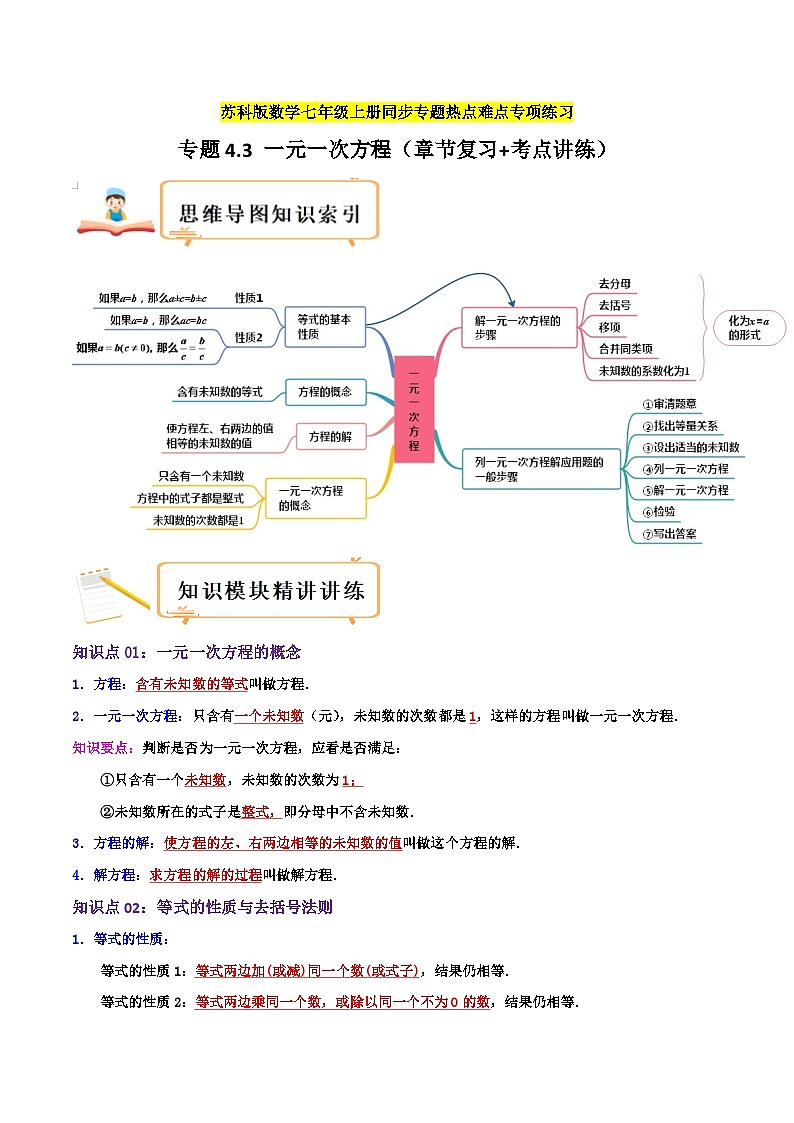
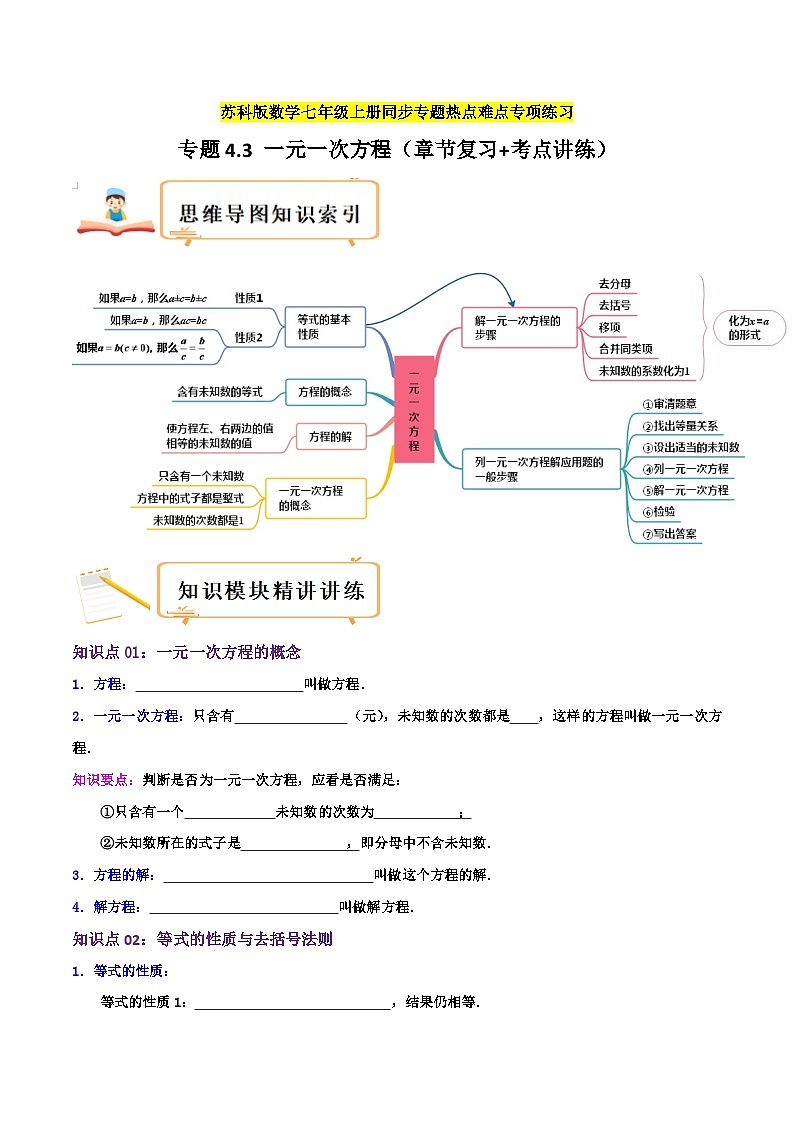
苏科版数学七年级上册期末复习专题4.3 一元一次方程（章节复习+考点讲练）（2份，原卷版+教师版）

这是一份苏科版数学七年级上册期末复习专题4.3 一元一次方程（章节复习+考点讲练）（2份，原卷版+教师版），文件包含苏科版数学七年级上册期末复习专题43一元一次方程章节复习+考点讲练教师版doc、苏科版数学七年级上册期末复习专题43一元一次方程章节复习+考点讲练学生版doc等2份试卷配套教学资源，其中试卷共49页， 欢迎下载使用。

知识点01：一元一次方程的概念
1．方程：含有未知数的等式叫做方程．
2．一元一次方程：只含有一个未知数（元），未知数的次数都是1，这样的方程叫做一元一次方程．
知识要点：判断是否为一元一次方程，应看是否满足：
①只含有一个未知数，未知数的次数为1；
②未知数所在的式子是整式，即分母中不含未知数．
3．方程的解：使方程的左、右两边相等的未知数的值叫做这个方程的解．
4．解方程：求方程的解的过程叫做解方程．
知识点02：等式的性质与去括号法则
1．等式的性质：
等式的性质1：等式两边加(或减)同一个数(或式子)，结果仍相等．
等式的性质2：等式两边乘同一个数，或除以同一个不为0的数，结果仍相等．
2．合并法则：合并时，把系数相加(减)作为结果的系数，字母和字母的指数保持不变．
3．去括号法则：
（1）括号外的因数是正数，去括号后各项的符号与原括号内相应各项的符号相同．
（2）括号外的因数是负数，去括号后各项的符号与原括号内相应各项的符号相反．
知识点03：一元一次方程的解法
解一元一次方程的一般步骤：
(1)去分母：在方程两边同乘以各分母的最小公倍数．
(2)去括号：依据乘法分配律和去括号法则，先去小括号，再去中括号，最后去大括号．
(3)移项：把含有未知数的项移到方程一边，常数项移到方程另一边．
(4)合并：逆用乘法分配律，分别合并含有未知数的项及常数项，把方程化为ax＝b(a≠0)的形式．
(5)系数化为1：方程两边同除以未知数的系数得到方程的解(a≠0)．
(6)检验：把方程的解代入原方程，若方程左右两边的值相等，则是方程的解；若方程左右两边的值不相等，则不是方程的解．
知识点04：用一元一次方程解决实际问题的常见类型
1.行程问题：路程＝速度×时间
2.和差倍分问题：增长量＝原有量×增长率
3.利润问题：商品利润＝商品售价－商品进价
4.工程问题：工作量＝工作效率×工作时间，各部分劳动量之和＝总量
5.银行存贷款问题：本息和＝本金+利息，利息＝本金×利率×期数
6.数字问题：多位数的表示方法：例如：.
【典例精讲】（2021秋•崇川区校级月考）小红在解关于x的方程：﹣3x+1＝3a﹣2时，误将方程中的“﹣3”看成了“3”，求得方程的解为x＝1，则原方程的解为 x＝﹣1 ．
【思路点拨】把x＝1代入3x+1＝3a﹣2，求出a的值，再把a的值代入原方程求解即可．
【规范解答】解：把x＝1代入3x+1＝3a﹣2，
得3+1＝3a﹣2，
解得a＝2，
故原方程为﹣3x+1＝6﹣2，
﹣3x＝3，
解得x＝﹣1．
故答案为：x＝﹣1．
【考点评析】本题考查了一元一次方程的解的定义．使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解．
【变式训练1-1】（2013秋•南长区期末）已知x＝2是关于x的方程3x+a＝0的一个解，则a的值是（ ）
A．﹣6B．﹣3C．﹣4D．﹣5
【思路点拨】方程的解就是能够使方程两边左右相等的未知数的值，即利用方程的解代替未知数，所得到的式子左右两边相等．
【规范解答】解：把x＝2代入方程得：6+a＝0，
解得：a＝﹣6．
故选：A．
【考点评析】本题主要考查了方程解的定义，已知x＝2是方程的解实际就是得到了一个关于a的方程．
【变式训练1-2】（2021秋•灌云县校级月考）已知x＝5是方程ax﹣8＝20+a的解，则a的值是（ ）
A．2B．3C．7D．8
【思路点拨】根据方程的解是使方程成立的未知数的值，把方程的解代入方程，可得答案．
【规范解答】解：把x＝5 代入方程ax﹣8＝20+a，
得：5a﹣8＝20+a，
解得：a＝7，
故选：C．
【考点评析】本题考查了方程的解，把方程的解代入方程，得关于a的一元一次方程，解一元一次方程，得答案．
【变式训练1-3】（2021秋•崇川区校级月考）方程2x+▲＝3x，▲处是被墨水盖住的常数，已知方程的解是x＝2，那么▲处的常数是 2 ．
【思路点拨】把x＝2代入已知方程，可以列出关于▲的方程，通过解该方程可以求得▲处的数字．
【规范解答】解：把x＝2代入方程，得4+▲＝6，
解得▲＝2．
故答案为：2．
【考点评析】此题考查的是一元一次方程的解的定义，就是能够使方程左右两边相等的未知数的值．
【变式训练1-4】（2022秋•鼓楼区月考）（1）数a，b在数轴上对应的A，B两点之间距离|AB|＝|a﹣b|．
（2）数轴上表示1和﹣3两点之间的距离是 4 ；
数轴上表示x和﹣2两点之间的距离是 |x+2| ．
（3）根据图象比较大小：|3+a| ＜ |﹣3﹣b|（填“＜”、“＝”、“＞”）．
（4）若点 A、B、C在数轴上分别表示数﹣1、4、c，且点C到点A、B的距离之和是7，则c＝ ﹣2或5 ．
（5）关于x的方程|x﹣m|+|x﹣n|＝k（m＞n，k＞0），借助数轴探究方程的解的情况，直接写出结论．
【思路点拨】（2）根据题中的两点间的距离公式求解；
（3）根据图形中的位置判断；
（4）根据题意列方程求解；
（5）分类讨论，解方程．
【规范解答】解：（2）|﹣3﹣1|＝4，|x﹣（﹣2）|＝|x+2|，
故答案为：4，|x+2|；
（3）∵|3+a|＝|﹣3﹣a|，
由图可得：|3+a|＜|﹣3﹣b|，
故答案为：＜；
（4）由题意得：|c+1|+|c﹣4|＝7，
解得：c＝﹣2或c＝5，
故答案为：﹣2或5；
（5）当x＜n时，m﹣x+n﹣x＝k，
解得x＝，
当n≤x≤m时，x﹣n+m﹣x＝k，
若m﹣n＝k，有无数个解，
当m﹣n≠k时，无解，
当x＞m时，x﹣m+x﹣n＝k，
解得：x＝．
【考点评析】本题考查了方程的解和数轴，数形结合思想和分类讨论思想是解题的关键．
【典例精讲】（2022秋•宿迁期中）下列说法：①若a为有理数，且a≠0，则a＜a2；②若＝a，则a＝1；③若a3+b3＝0，则a，b互为相反数；④若|a|＝﹣a，则a＜0．其中正确说法是 ③ （填序号）．
【思路点拨】根据有理数的乘方、等式的性质、相反数、绝对值解决此题．
【规范解答】解：①根据有理数的乘方，当a＝，则，此时，即a＞a2，故①不正确．
②根据等式的性质，若＝a，则a＝±1，故②不正确．
③根据有理数的乘方以及相反数的定义，由a3+b3＝0，得a3＝﹣b3，推断出a3＝（﹣b）3，则a＝﹣b，即a，b互为相反数，故③正确．
④根据绝对值的定义，由|a|＝﹣a≥0，得a≤0，故④不正确．
综上：正确的有③．
故答案为：③．
【考点评析】本题主要考查有理数的乘方、等式的性质、相反数、绝对值，熟练掌握有理数的乘方、等式的性质、相反数、绝对值是解决本题的关键．
【变式训练2-1】（2022秋•宿城区期中）已知等式a＝b，则下列等式中不一定成立的是（ ）
A．a+1＝b+1B．2a﹣2b＝0C．D．ac＝bc
【思路点拨】根据等式的性质，等式的两边都加或都减同一个整式，结果不变，等式的两边都乘以或除以同一个不为零的整式，结果不变，可得答案．
【规范解答】解；A、两边都加1，故A正确，不符合题意；
B、两边都乘以2，故B正确，不符合题意；
C、当c＝0时，无意义故C错误，符合题意；
D、两边都乘以c时，故D正确，不符合题意；
故选：C．
【考点评析】本题考查了等式的性质，注意等式的两边都除以同一个不为零的数，结果不变．
【变式训练2-2】（2022秋•苏州期中）如图，●，■，▲分别表示三种不同的物体，前两架天平保持平衡，如果要使第三架天平也保持平衡，那么第三架天平的右边应放的物体是（ ）
A．■■B．■■■C．■■■■D．■■■■■
【思路点拨】根据等式的性质得出，●，■，▲三个图形之间的关系即可．
【规范解答】解：由题意知，在第二个天平两边都加入一个■，对比第一个天平即可得出●＝■■，
把第二个天平中的●换成■■，则▲＝■■■，
∴●▲＝■■■■■，
故选：D．
【考点评析】本题主要考查等式的性质，熟练掌握等式的性质是解题的关键．
【变式训练2-3】（2021秋•泰州期末）我们知道，借助天平和一些物品可以探究得到等式的基本性质．
【提出问题】能否借助一架天平和一个10克的砝码测量出一个乒乓球和一个一次性纸杯的质量？
【实验探究】准备若干相同的乒乓球和若干相同的一次性纸杯（每个乒乓球的质量相同，每个纸杯的质量也相同），设一个乒乓球的质量是x克，经过试验，将有关信息记录在下表中：
【解决问题】
（1）将表格中两个空白部分用含x的代数式表示；
（2）分别求出一个乒乓球的质量和一个一次性纸杯的质量．
【及时迁移】借助以上相关数据以及实验经验，你能设计一种方案，使实验中选取的乒乓球和纸杯的个数一样多吗？请补全下面横线上内容，完善方案，并说明方案设计的合理性．
方案：将天平左边放置 10个乒乓球 ，天平右边放置 10个一次性纸杯和1个10克的砝码 ，使得天平平衡．
理由：
【思路点拨】解决问题：（1）用乒乓球的总质量加上砝码的总质量可得答案；
（2）根据题意列出方程，求解可得答案；
及时迁移：根据乒乓球、纸杯、砝码的质量设计即可，只是平衡即可．
【规范解答】解：（1）根据题意可得：记录一中的一次性纸杯的总质量为：6x+10；
记录二中的一次性纸杯的总质量为：4x﹣10，
故答案为：6x+10；4x﹣10，
（2）由题意得：6x+10＝14（4x﹣10），
解得：x＝3，∴4x﹣10＝2
答：一个乒乓球的质量为3克，一个一次性纸杯的质量为2克．
及时迁移：将天平左边放置10个乒乓球，天平右边放置10个一次性纸杯和1个10克的砝码，使得天平平衡．
故答案为：10个乒乓球，10个一次性纸杯和1个10克的砝码，
理由：不唯一，算术方法或者方程方法说明都可以，言之有理即可．
【考点评析】此题考查的是等式的性质、列代数式，掌握等式两边加同一个数（或式子）结果仍得等式；等式两边乘同一个数或除以一个不为零的数，结果仍得等式是解决此题的关键．
【典例精讲】（2022秋•亭湖区期末）若（2﹣a）x|a﹣1|﹣5＝0是关于x的一元一次方程，则a＝ 0 ．
【思路点拨】依据只含有一个未知数（元），且未知数的次数是1，这样的方程叫一元一次方程，列出关于a的不等式与方程求解即可．
【规范解答】解：（2﹣a）x|a﹣1|﹣5＝0是关于x的一元一次方程，
∴2﹣a≠0且|a﹣1|＝1，
解得：a＝0．
故答案为：0．
【考点评析】本题主要考查的是一元一次方程的定义，依据一元一次方程的定义列出关于a的不等式组是解题的关键．
【变式训练3-1】（2022秋•滨海县月考）下列方程中，是一元一次方程的是（ ）
A．x﹣y＝6B．x2+x﹣3＝0C．4x＝24D．
【思路点拨】根据一元一次方程的定义即可求出答案．只含有一个未知数（元），且未知数的次数是1，这样的整式方程叫一元一次方程．
【规范解答】解：A．x﹣y＝6中有两个未知数，不是一元一次方程，故本选项不符合题意；
B．x2+x﹣3＝0，不是一元一次方程，故本选项不符合题意；
C．4x＝24，是一元一次方程，故本选项符合题意；
D．﹣1＝24，不是一元一次方程，故本选项不符合题意．
故选：C．
【考点评析】本题考查一元一次方程的定义，解题的关键是正确运用一元一次方程的定义，本题属于基础题型．
【变式训练3-2】（2019秋•东台市期中）若关于x的方程mxm﹣2﹣m+3＝0是一元一次方程，则这个方程的解是（ ）
A．x＝0B．x＝3C．x＝﹣3D．x＝2
【思路点拨】只含有一个未知数（元），并且未知数的指数是1（次）的方程叫做一元一次方程，它的一般形式是ax+b＝0（a，b是常数且a≠0），高于一次的项系数是0．
【规范解答】解：由一元一次方程的特点得m﹣2＝1，即m＝3，
则这个方程是3x＝0，
解得：x＝0．
故选：A．
【考点评析】本题主要考查了一元一次方程的一般形式，只含有一个未知数，未知数的指数是1，一次项系数不是0，这是这类题目考查的重点．
【变式训练3-3】（2015秋•扬州校级月考）已知：（a+2b）y2﹣＝3是关于y的一元一次方程．
（1）求a、b的值；
（2）若x＝a是方程﹣+3＝x﹣的解，求|a﹣b﹣2|﹣|b﹣m|的值．
【思路点拨】（1）先根据一元一次方程的定义列出关于a，b的方程组，求出a，b的值即可；
（2）把x＝a代入方程求出m的值，再代入代数式求解即可．
【规范解答】解：（1）∵（a+2b）y2﹣＝3是关于y的一元一次方程，
∴，解得；
（2）∵a＝4，x＝a是方程﹣+3＝x﹣的解，
∴1﹣+3＝4﹣，解得m＝﹣，
∴|a﹣b﹣2|﹣|b﹣m|＝|4+2﹣2|﹣|﹣2+|＝．
【考点评析】本题考查的是一元一次方程的定义，熟知只含有一个未知数（元），且未知数的次数是1，这样的方程叫一元一次方程是解答此题的关键．
【变式训练3-4】（2017秋•广陵区校级月考）已知关于x的方程（m+3）x|m+4|+18＝0是一元一次方程，试求：
（1）m的值；
（2）2（3m+2）﹣3（4m﹣1）的值．
【思路点拨】（1）根据一元一次方程的定义求解即可；
（2）根据代数式求值，可得答案．
【规范解答】解：（1）由题意，得
|m+4|＝1且m+3≠0，
解得m＝﹣5．
（2）当m＝﹣5时，2（3m+2）﹣3（4m﹣1）＝2×（﹣15+2）﹣3（﹣20﹣1）＝﹣26+63＝37．
【考点评析】本题主要考查了一元一次方程的一般形式，只含有一个未知数，未知数的指数是1，一次项系数不是0，这是这类题目考查的重点．
【典例精讲】（2022秋•海门市期末）若关于x的方程5x﹣1＝2x+a的解与方程4x+3＝7的解互为相反数，则a＝ ﹣4 ．
【思路点拨】求出第二个方程的解的相反数，代入第一个方程计算即可求出a的值．
【规范解答】解：方程4x+3＝7，
移项合并得：4x＝4，
解得：x＝1，
把x＝﹣1代入5x﹣1＝2x+a得：﹣6＝﹣2+a，
解得：a＝﹣4，
故答案为：﹣4
【考点评析】此题考查了一元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值．
【变式训练4-1】（2022秋•如皋市校级期末）已知关于x的方程3x﹣5＝x+a的解是x＝2，则a的值等于（ ）
A．﹣2B．﹣1C．2D．1
【思路点拨】将x＝2代入3x﹣5＝x+a，再解出a即可．
【规范解答】解：将x＝2代入3x﹣5＝x+a，
得：3×2﹣5＝2+a，
解得：a＝﹣1．
故选：B．
【考点评析】本题考查方程的解的定义．掌握方程的解就是使等式成立的未知数的值是解题关键．
【变式训练4-2】（2021秋•宜兴市校级月考）方程5y﹣7＝2y﹣中被阴影盖住的是一个常数，此方程的解是y＝﹣1．这个常数应是（ ）
A．10B．4C．﹣4D．﹣10
【思路点拨】将y＝﹣1代入方程计算可求解这个常数．
【规范解答】解：将y＝﹣1代入方程5y﹣7＝2y﹣中，
5×（﹣1）﹣7＝2×（﹣1）﹣，
解得＝10，
故选：A．
【考点评析】本题主要考查一元一次方程的解，理解一元一次方程解的概念是解题的关键．
【变式训练4-3】（2022秋•丹徒区期末）已知关于m的方程的解也是关于x的方程2（x﹣8）﹣n＝6的解．
（1）求m、n的值；
（2）如图，数轴上，O为原点，点M对应的数为m，点N对应的数为n．
①若点P为线段ON的中点，点Q为线段OM的中点，求线段PQ的长度；
②若点P从点N出发以1个单位/秒的速度沿数轴正方向运动，点Q从点M出发以2个单位/秒的速度沿数轴负方向运动，经过 3或5 秒，P、Q两点相距3个单位．
【思路点拨】（1）解方程求出m＝10的值，再把x＝10代入方程即可得出n的值；
（2）①根据线段中点的定义求出OP和OQ的长度即可得出答案；
②设运动时间为x秒，列方程解答即可．
【规范解答】解：（1）解方程得，m＝10，
∵方程2（x﹣8）﹣n＝6的解为x＝10，
∴4﹣n＝6，
解得n＝﹣2，
∴m、n的值分别为10，﹣2；
（2）①∵点M对应的数为10，点N对应的数为﹣2，点P为线段ON的中点，点Q为线段OM的中点，
∴OP＝ON＝1，OQ＝OM＝5，
∴PQ＝OP+OQ＝1+5＝6；
②设经过x秒P、Q两点相距3个单位，
根据题意得：﹣2+x﹣（10﹣2x）＝3或（10﹣2x）﹣（﹣2+x）＝3，
解得x＝5或x＝3，
故经过3秒或5秒，A、B两点相距3个单位．
故答案为：3或5．
【考点评析】本题考查了数轴和一元一次方程的应用，解题的关键是到达题意，用含字母的式子表示P，Q所表示的数．
【变式训练4-4】（2022秋•鼓楼区校级期末）我们规定，关于x的一元一次方程mx＝n（m≠0）的解为x＝m+n，则称该方程为和解方程，例如2x＝﹣4的解为x＝﹣2＝﹣4+2，则方程为和解方程．
请根据上边规定解答下列问题：
（1）下列关于x的一元一次方程是“和解方程”的有 ② ．
①；②；③5x＝﹣2．
（2）若关于x的一元一次方程3x＝2a﹣10是和解方程，则a＝ ．
（3）关于x的一元一次方程3x＝a+b是和解方程，则代数式a（a2b+1）+b（1﹣a3）的值为 ﹣ ．
（4）关于x的一元一次方程3x＝a+b是和解方程且它的解为x＝a，求代数式2ab（a+b）的值．
【思路点拨】（1）根据“和解方程”的定义进行判断即可；
（2）根据“和解方程”的定义得到关于a的方程，解之即可；
（3）根据“和解方程”的定义得到，将所求式子化简后整体代入即可；
（4）根据已知条件得到，可求出a，b值，代入计算即可．
【规范解答】解：（1）①的解是，故不是“和解方程”；
②的解是，故是“和解方程”；
③5x＝﹣2的解是，故不是“和解方程”；
故答案为：②；
（2）∵3x＝2a﹣10是和解方程，
∴，
解得：，
故答案为：；
（3）∵3x＝a+b是和解方程，
∴，
化简得：，
∴a（a2b+1）+b（1﹣a3）＝a3b+a+b﹣a3b＝a+b＝，
故答案为：﹣；
（4）∵3x＝a+b是和解方程且它的解为x＝a，
∴，
∴解得：，b＝﹣3，
∴．
【考点评析】本题考查了一元一次方程的解，代数式求值，掌握解一元一次方程的步骤是解题的关键．
【典例精讲】．（2022秋•滨海县月考）对于任意有理数a，b，我们规定：a⊗b＝a2﹣2b，例如：3⊗4＝32﹣2×4＝9﹣8＝1．若2⊗x＝3+x，则x的值为 ．
【思路点拨】先根据新运算得出算式，再根据等式的性质求出方程的解即可．
【规范解答】解：∵2⊗x＝3+x，
∴22﹣2x＝3+x，
∴4﹣2x＝3+x，
∴﹣2x﹣x＝3﹣4，
∴﹣3x＝﹣1，解得x＝．
故答案为：．
【考点评析】本题考查了解一元一次方程和有理数的混合运算，能根据题意列出关于x的一元一次方程是解题的关键．
【变式训练5-1】（2022秋•海门市期末）解方程时，去分母正确的是（ ）
A．2x+1﹣（10x+1）＝1B．4x+1﹣10x+1＝6
C．4x+2﹣10x﹣1＝6D．2（2x+1）﹣（10x+1）＝1
【思路点拨】去分母的方法是方程两边同时乘以各分母的最小公倍数6，在去分母的过程中注意分数线右括号的作用，以及去分母时不能漏乘没有分母的项．
【规范解答】解：方程两边同时乘以6得：4x+2﹣（10x+1）＝6，
去括号得：4x+2﹣10x﹣1＝6．
故选：C．
【考点评析】在去分母的过程中注意分数线起到括号的作用，并注意不能漏乘没有分母的项．
【变式训练5-2】（2017秋•秦淮区期末）下列方程变形中，正确的是（ ）
A．由3x＝﹣4，系数化为1得x＝
B．由5＝2﹣x，移项得x＝5﹣2
C．由 ，去分母得4（x﹣1）﹣3（2x+3）＝1
D．由 3x﹣（2﹣4x）＝5，去括号得3x+4x﹣2＝5
【思路点拨】根据解方程的方法和等式的性质可以判断各个选项是否正确，从而可以解答本题．
【规范解答】解：3x＝﹣4，系数化为1，得x＝﹣，故选项A错误，
5＝2﹣x，移项，得x＝2﹣5，故选项B错误，
由，去分母，得4（x﹣1）﹣3（2x+3）＝24，故选项C错误，
由 3x﹣（2﹣4x）＝5，去括号得，3x﹣2+4x＝5，故选项D正确，
故选：D．
【考点评析】本题考查解一元一次方程、等式的性质，解答本题的关键是明确解方程的方法．
【变式训练5-3】（2022秋•鼓楼区校级期末）整式ax﹣b的值随x的取值不同而不同，下表是当x取不同值时对应的整式的值，则关于x的方程﹣ax+b＝3的解是 x＝0 ．
【思路点拨】把x与ax﹣b的值的方程组成方程组，求出方程组的解得到a与b的值，即可求出方程的解．
【规范解答】解：根据表格得：，
把②代入①得：﹣2a+3＝﹣6，
解得：a＝，
∴方程为﹣x+3＝3，
解得：x＝0．
故答案为：x＝0．
【考点评析】此题考查了解一元一次方程，二元一次方程组，以及代数式求值，熟练掌握各自的解法是解本题的关键．
【变式训练5-4】（2020秋•惠山区期中）解方程：
（1）3x+7＝32﹣2x；
（2）．
【思路点拨】（1）移项、合并同类项、系数化为1，据此求出方程的解是多少即可．
（2）去分母、去括号、移项、合并同类项、系数化为1，据此求出方程的解是多少即可．
【规范解答】解：（1）移项，可得：3x+2x＝32﹣7，
合并同类项，可得：5x＝25，
系数化为1，可得：x＝5．
（2）去分母，可得：3（3x﹣1）﹣12＝2（5x﹣7），
去括号，可得：9x﹣3﹣12＝10x﹣14，
移项，合并同类项，可得：x＝﹣1．
【考点评析】此题主要考查了解一元一次方程的方法，要熟练掌握，解一元一次方程的一般步骤：去分母、去括号、移项、合并同类项、系数化为1．
【变式训练5-5】（2022秋•丹徒区期末）解方程：
（1）3（2x﹣1）+1＝4（x+2）；
（2）．
【思路点拨】（1）方程去括号，移项，合并同类项，把x系数化为1，即可求出解；
（2）方程去分母，去括号，移项，合并同类项，把x系数化为1，即可求出解．
【规范解答】解：（1）去括号得：6x﹣3+1＝4x+8，
移项得：6x﹣4x＝8+3﹣1，
合并同类项得：2x＝10，
解得：x＝5；
（2）去分母得：2（2x﹣1）＝2x+1﹣6，
去括号得：4x﹣2＝2x+1﹣6，
移项得：4x﹣2x＝1﹣6+2，
合并同类项得：2x＝﹣3，
解得：x＝﹣1.5．
【考点评析】此题考查了解一元一次方程，熟练掌握一元一次方程的解法是解本题的关键．
【典例精讲】（2022秋•海陵区校级月考）已知关于x的方程|x+1|＝a﹣2只有一个解，那么xa＝ 1 ．
【思路点拨】根据题意计算出a，x的值，再计算xa的值．
【规范解答】解：∵关于x的方程|x+1|＝a﹣2只有一个解，
∴a﹣2＝0，a＝2，
∴x+1＝0，
∴x＝﹣1，
∴（﹣1）2＝1，
故答案为：1．
【考点评析】本题考查了含绝对值的一元一次方程，解题的关键是掌握绝对值的定义，解一元一次方程．
【变式训练6-1】（2022秋•张家港市期中）已知c为实数，讨论方程|x﹣1|﹣|x﹣2|+2|x﹣3|＝c解的情况．
【思路点拨】分类讨论：x＜1，1≤x＜2，2≤x＜3，x≥3，根据绝对值的性质，可化简绝对值，根据解方程，可得答案．
【规范解答】解：当x＜1时，原方程等价于1﹣x﹣（2﹣x）+2（3﹣x）＝c，
X＝，，否则无解．
当1≤x＜2时，原方程等价于x﹣1﹣（2﹣x）+2（3﹣x）＝c
C＝3时，解为：1≤X＜2．否则无解．
当2≤x＜3时，原方程等价于x﹣1﹣（x﹣2）+2（3﹣x）＝c，
X＝，2时有解，此时：1＜C≤3有解：X＝，否则无解，
当x≥3时，原方程等价于x﹣1﹣（x﹣2）+2（x﹣3）＝c，
X＝，时有解，此时：c≥1，有解：X＝，否则无解，
综上所述：c≥1方程有解，c＜1方程无解．
【考点评析】本题目考查绝对值方程，需要讨论，把绝对值方程转化为一般的一元一次方程求解，体现了转换的数学思想．
【变式训练6-2】（2022秋•鼓楼区校级月考）【我阅读】
解方程：|x+5|＝2．
解：当x+5≥0时，原方程可化为：x+5＝2，解得x＝﹣3；
当x+5＜0时，原方程可化为：x+5＝﹣2，解得x＝﹣7．
所以原方程的解是x＝﹣3或x＝﹣7．
【我会解】
解方程：|3x﹣2|﹣5＝0．
【思路点拨】类比题干的解题过程，先根据绝对值的定义去掉绝对值符号，再解一元一次方程即可．
【规范解答】解：当3x﹣2≥0时，原方程可化为：3x﹣2﹣5＝0，
解得x＝；
当3x﹣2＜0时，原方程可化为：﹣3x+2﹣5＝0，
解得x＝﹣1．
所以原方程的解是x＝或x＝﹣1．
【考点评析】本题考查绝对值的定义以及解一元一次方程，解题的关键是根据绝对值的定义将绝对值符号去掉，从而化为一般的一元一次方程求解．
【变式训练6-3】（2022秋•高新区校级月考）小兵喜欢研究数学问题，在学习一元一次方程后，他给出一个新定义：若x0是关于x的一元一次方程ax+b＝0的解，y0是关于y的方程的所有解的其中一个解，且x0，y0满足x0+y0＝100，则称关于y的方程为关于x的一元一次方程的“友好方程”．例如：一元一次方程3x﹣2x﹣99＝0的解是x＝99，方程y2+1＝2的所有解是y＝1或y＝﹣1，当y0＝1时，x0+y0＝100，所以y2+1＝2为一元一次方程3x﹣2x﹣99＝0的“友好方程”．
（1）已知关于y的方程：①2y﹣2＝4，②|y|＝2，哪个方程是一元一次方程3x﹣2x﹣102＝0的“友好方程”？请直接写出正确的序号是 ② ．
（2）若关于y的方程|2y﹣2|+3＝5是关于x的一元一次方程x﹣＝a+1的“友好方程”，请求出a的值．
【思路点拨】（1）根据友好方程定义判断．
（2）根据友好方程的条件列出关于a的方程．
【规范解答】解：（1）方程①的解为：y＝3，方程②的解为：y＝±2，
方程3x﹣2x﹣102＝0的解为：x＝102．
∵3+102≠100，﹣2+102＝100．
∴方程①不是方程3x﹣2x﹣102＝0的友好方程，方程②是方程3x﹣2x﹣102＝0的友好方程．
故答案为：②．
（2）∵|2y﹣2|+3＝5．
|2y﹣2|＝2，
∴2y﹣2＝2或2y﹣2＝﹣2．
∴y＝2或y＝0．
∵方程x﹣＝a+1，
∴3x﹣2x+2a＝3a+3．
∴x＝a+3．
∵两个方程是友好方程，
∴2+a+3＝100或0+a+3＝100．
∴a＝95或a＝97．
【考点评析】本题考查新定义解决数学问题，理解新定义是求解本题的关键．
【典例精讲】（2022秋•海陵区校级期末）如果方程的解与方程4x﹣（3a+1）＝6x+2a﹣1的解相同，则代数式a﹣的值为 ﹣ ．
【思路点拨】先解关于x的方程得出x＝10，将其代入方程4x﹣（3a+1）＝6x+2a﹣1求得a的值，继而代入计算可得．
【规范解答】解：解方程得x＝10，
将x＝10代入4x﹣（3a+1）＝6x+2a﹣1得：40﹣3a﹣1＝60+2a﹣1，
解得：a＝﹣4，
则原式＝﹣，
故答案为：﹣．
【考点评析】本题主要考查方程的解，解题的关键是掌握方程的解的概念和解一元一次方程的能力．
【变式训练7-1】（2022秋•惠山区校级期末）关于x的方程kx＝2x+6与2x﹣1＝5的解相同，则k的值为（ ）
A．4B．3C．5D．6
【思路点拨】先解2x﹣1＝5得出x＝3，代入kx＝2x+6即可求解．
【规范解答】解：2x﹣1＝5，
解得：x＝3，
代入kx＝2x+6，
即3k＝6+6，
解得：k＝4．
故选：A．
【考点评析】本题考查了一元一次方程的解，解一元一次方程，掌握一元一次方程的解的定义是解题的关键．
【变式训练7-2】（2022秋•姑苏区校级期末）若关于x的方程＝5与kx﹣1＝15的解相同，则k的值为（ ）
A．8B．6C．﹣2D．2
【思路点拨】先解出第一个方程的解，代入到第二个方程中，求出k的值．
【规范解答】解：＝5，
∴2x﹣1＝15，
∴x＝8；
把x＝8代入第二个方程得：8k﹣1＝15，
解得：k＝2．
故选：D．
【考点评析】本题考查了同解方程，一元一次方程的解法，考核学生的计算能力，将第一个方程的解代入第二个方程是解题的关键．
【变式训练7-3】（2017秋•崇川区校级月考）如果关于x的方程与的解相同，那么m的值是 ±2 ．
【思路点拨】本题中有两个方程，且是同解方程，一般思路是：先求出不含字母系数的方程的解，再把解代入到含有字母系数的方程中，求字母系数的值．
【规范解答】解：解方程＝
整理得：15x﹣3＝42，
解得：x＝3，
把x＝3代入＝x+4+2|m|
得＝3++2|m|
解得：|m|＝2，
则m＝±2．
故答案为±2．
【考点评析】本题考查了同解方程，使方程左右两边相等的未知数的值是该方程的解，因此检验一个数是否为相应的方程的解，就是把这个数代替方程中的未知数，看左右两边的值是否相等．
【变式训练7-4】．（2021秋•广陵区校级期末）已知方程6x﹣9＝10x﹣5与方程3a﹣1＝3（x+a）﹣2a的解相同；
（1）求这个相同的解；
（2）求a的值．
【思路点拨】（1）根据移项、合并同类项、系数化为1，可得答案；
（2）根据同解方程，可得关于a的方程，根据解方程，可得答案．
【规范解答】解：（1）6x﹣9＝10x﹣5
移项，得：
6x﹣10x＝﹣5+9，
合并同类项，得：
﹣4x＝4，
系数化为1，得：
x＝﹣1．
（2）由方程6x﹣9＝10x﹣5与方程3a﹣1＝3（x+a）﹣2a的解相同，得
3a﹣1＝3（﹣1+a）﹣2a，
解得a＝﹣1．
【考点评析】本题考查了同解方程，利用同解方程的出关于a的方程是解题关键．
【变式训练7-5】（2022秋•滨海县月考）已知关于的方程2﹣＝+3﹣x与方程4﹣＝3k﹣的解相同，求k的值．
【思路点拨】先解方程2﹣＝+3﹣x，可得x＝1，然后再把x＝1代入方程4﹣＝3k﹣中得：4﹣＝3k﹣，最后进行计算即可解答．
【规范解答】解：2﹣＝+3﹣x，
12﹣2（x﹣1）＝3（1﹣x）+18﹣6x，
12﹣2x+2＝3﹣3x+18﹣6x，
﹣2x+3x+6x＝3+18﹣12﹣2，
7x＝7，
x＝1，
由题意得：
把x＝1代入方程4﹣＝3k﹣中得：
4﹣＝3k﹣，
4﹣＝3k，
12﹣（k+2）＝9k，
12﹣k﹣2＝9k，
﹣k﹣9k＝2﹣12，
﹣10k＝﹣10，
k＝1，
∴k的值为1．
【考点评析】本题考查了同解方程，熟练掌握同解方程的意义是解题的关键．
【典例精讲】（2022秋•如皋市校级期末）《九章算术》中记载了这样一个数学问题：今有甲发长安，五日至齐；乙发齐，七日至长安．今乙发已先二日，甲仍发长安．问几何日相逢？译文：甲从长安出发，5日到齐国；乙从齐国出发，7日到长安．现乙先出发2日，甲才从长安出发．问多久后甲乙相逢？设乙出发x日，甲乙相逢，则可列方程（ ）
A．B．C．D．
【思路点拨】根据题意设乙出发x日，甲乙相逢，则甲、乙分别所走路程占总路程的和，进而得出等式．
【规范解答】解：设乙出发x日，甲乙相逢，则甲出发（x﹣2）日，故可列方程为：
+＝1．
故选：D．
【考点评析】此题主要考查了由实际问题抽象出一元一次方程，正确表示出两人所走路程所占比是解题关键．
【变式训练8-1】（2022秋•滨海县月考）有一些相同的房间需要粉刷墙面．一天3名一级技工去粉刷8个房间，结果其中有50m2墙面未来得及粉刷，同样时间内5名二级技工粉刷了10个房间之外，还多粉刷了另外的40m2墙面，每名一级技工比二级技工一天多粉刷10m2墙面．设每名二级技工一天粉刷墙面xm2，则列方程为（ ）
A．B．
C．D．
【思路点拨】设每名二级技工一天粉刷墙面xm2，则每名一级技工一天粉刷（x+10）m2墙面，即可得出关于x的一元一次方程．
【规范解答】解：设每名二级技工一天粉刷墙面xm2，则每名一级技工一天粉刷（x+10）m2墙面，
依题意，得：＝．
故选：A．
【考点评析】本题考查了由实际问题抽象出一元一次方程，找准等量关系，正确列出一元一次方程是解题的关键．
【变式训练8-2】（2021秋•如东县期中）我国明代数学读本《算法统宗》一书中有这样一道题：“一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托”．其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺．如果1托为5尺，那么索和竿各为几尺？设竿为x尺，可列方程为 （x+5）＝x﹣5 ．
【思路点拨】设竿为x尺，则索为（x+5）尺，根据“一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托”，即可得出关于x一元一次方程．
【规范解答】解：设竿为x尺，则索为（x+5）尺，
根据题意得：（x+5）＝x﹣5，
故答案为：（x+5）＝x﹣5．
【考点评析】本题考查了一元一次方程的应用，找准等量关系是解题的关键．
【变式训练8-3】（2022秋•江宁区月考）新年将至，乐乐和丽丽所在的活动小组计划做一批“中国结”．如果每人做8个，那么比计划多了3个；如果每人做5个，那么比计划少27个．问题：该小组共有多少人？计划做多少个“中国结”？
她俩经过独立思考后，分别列出了如下尚不完整的方程：
乐乐的方法：8x□ ﹣3 ＝5x□ +27 ；
丽丽的方法：；
（1）在乐乐、丽丽所列的方程中，“□”中是运算符号，“”中是数字，试分别指出未知数x，y表示的意义：未知数x表示 该小组人数 ，未知数y表示 计划做“中国结”的个数 ；
（2）分别用这两种方法，将原题中的问题解答完成．
【思路点拨】（1）乐乐的方法是根据做“中国结”的个数不变列的方程，丽丽的方法是根据该小组的人数不变列的方程；
（2）可设该小组有x人，根据做“中国结”的个数不变先列出方程，再求解作答．
【规范解答】解：（1）﹣3；+27；未知数x表示的是该小组人数；未知数y表示的是计划做“中国结”的个数；
故答案为：﹣3；+27；该小组人数；计划做“中国结”的个数；
（2）设该小组有x人，
由题意得8x﹣3＝5x+27，
解这个方程，得x＝10，
计划做“中国结”的个数：8×10﹣3＝77（个）．
答：该小组共有10人，计划做“中国结”77个．
【考点评析】本题考查了列一元一次方程解决实际问题，掌握解一元一次方程应用题的一般步骤是关键．
【变式训练8-4】（2018秋•亭湖区校级期末）生态公园计划在园内的坡地上种植一片有A、B两种树的混合林，需要购买这两种树苗共100棵．假设这批树苗种植后成活95棵，种植A、B两种树苗的相关信息如下表：
（1）设购买A种树苗x棵，则购买B种树苗 （100﹣x） 棵，根据题意可列方程为 96%x+92%（100﹣x）＝95 ，解得x＝ 75 ．
（2）求种植这片混合林的总费用需多少元？
【思路点拨】（1）设购买A种树苗x棵，则购买B种树苗（100﹣x）棵，根据成活棵数＝种植A种树苗的棵数×成活率+种植B种树苗的棵数×成活率，即可得出关于x的一元一次方程，解之即可得出结论；
（2）根据总费用＝（A种树苗的单价+种植A种树苗的栽树劳务费）×种植A种树苗的棵数+（B种树苗的单价+种植B种树苗的栽树劳务费）×种植B种树苗的棵数，即可求出种植这片混合林的总费用．
【规范解答】解：（1）设购买A种树苗x棵，则购买B种树苗（100﹣x）棵，
依题意，得：96%x+92%（100﹣x）＝95，
解得：x＝75．
故答案为：（100﹣x）；96%x+92%（100﹣x）＝95；75．
（2）（15+3）×75+（20+4）×（100﹣75）＝1950（元）．
答：种植这片混合林的总费用需1950元．
【考点评析】本题考查了由实际问题抽象出一元一次方程，解题的关键是：（1）找准等量关系，正确列出一元一次方程；（2）根据数量关系，列式计算．
【变式训练8-5】（2021秋•姜堰区校级月考）为打造绿色生态环境，一段长为2400米的河道整治任务交由甲、乙两个工程队接力完成，共用时80天．已知甲队每天整治32米，乙队每天整治24米．
（1）根据题意，小李、小张分别列出如下的一元一次方程（尚不完整）：
小李：32x+24（ 80﹣x ）＝2400；
小张：＝80；
请分别指出上述方程中的意义，并补全方程：
小李：x表示 甲队工作的时间 ；
小张：x表示 甲队整治河道的长度 ．
（2）求甲、乙两队分别整治河道多少米？（写出完整的解答过程）
【思路点拨】（1）根据所列方程可得第一个方程为32x+24（80﹣x）＝2400，x表示的是甲队工作的时间，第二个方程为+＝80，x表示的是甲队整治河道的长度；
（2）求解第二个方程即可．
【规范解答】解：（1）由题意得，第一个方程为32x+24（80﹣x）＝2400，
x表示的是甲队工作的时间，
第二个方程为+＝80，
x表示的是甲队整治河道的长度，
故答案为：80﹣x，甲队工作的时间，甲队整治河道的长度；
（2）设甲队整治河道的长度为x米，
列方程得：+＝80，
解得：x＝1920，
则2400﹣x＝480．
答：甲、乙两队分别整治河道1920米，480米．
【考点评析】本题考查了一元一次方程的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程求解．
【典例精讲】（2021秋•如皋市校级月考）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有善行者行一百步，不善行者行六十步．今不善行者先行八十步，善行者追之，问几何步及之？“其意思为：速度快的人走100步，速度慢的人只走60步，现速度慢的人先走80步，速度快的人去追赶，则速度快的人要走 200 步才能追到速度慢的人．
【思路点拨】设速度快的人追上速度慢的人所用时间为t，根据速度慢的人和速度快的人所用时间相等列方程，求出时间，进而求出速度快的人所走的路程即可．
【规范解答】解：设速度快的人追到速度慢的人所用时间为t，
根据题意列方程得：100t＝60t+80，
解得t＝2，
2×100＝200（步），
∴速度快的人要走200步才能追到速度慢的人，
故答案为：200．
【考点评析】本题主要考查一元一次方程的知识，根据等量关系列出方程并正确求解是解题的关键．
【变式训练9-1】（2019秋•镇江期末）某超市在“元旦”活动期间，推出如下购物优惠方案：
①一次性购物在100元（不含100元）以内，不享受优惠；
②一次性购物在100元（含100元）以上，350元（不含350元）以内，一律享受九折优惠；
③一次性购物在350元（含350元）以上，一律享受八折优惠；
小敏在该超市两次购物分别付了90元和270元，如果小敏把这两次购物改为一次性购物，则小敏至少需付款（ ）元
A．288B．296C．312D．320
【思路点拨】设第一次购物购买商品的价格为x元，第二次购物购买商品的价格为y元，分0＜x＜100及100≤x＜350两种情况可得出关于x的一元一次方程，解之可求出x的值，由第二次购物付款金额＝0.9×第二次购物购买商品的价格可得出关于y的一元一次方程，解之可求出y值，再利用两次购物合并为一次购物需付款金额＝0.8×两次购物购买商品的价格之和，即可求出结论．
【规范解答】解：设第一次购物购买商品的价格为x元，第二次购物购买商品的价格为y元，
当0＜x＜100时，x＝90；
当100≤x＜350时，0.9x＝90，
解得：x＝100；
∵0.9y＝270，
∴y＝300．
∴0.8（x+y）＝312或320．
所以至少需要付312元．
故选：C．
【考点评析】此题主要考查了一元一次方程的应用，解题关键是第一次购物的90元可能有两种情况，需要讨论清楚．本题要注意不同情况的不同算法，要考虑到各种情况，不要丢掉任何一种．
【变式训练9-2】（2022秋•邗江区期末）某商店换季准备打折出售，若按照原售价的八折出售，将亏损20元，而按原售价的九折出售，将盈利10元，则该商品的成本为（ ）
A．230元B．250元C．260元D．300元
【思路点拨】设该商品的原售价为x元，根据成本不变列出方程，求出方程的解，然后再由打折即可得到结果．
【规范解答】解：设该商品的原售价为x元，
根据题意得：80%x+20＝90%x﹣10，
解得：x＝300，
则该商品的原售价为300元．
该商品的成本为：300×80%+20＝260，
故选：C．
【考点评析】此题考查了一元一次方程的应用，弄清题中的等量关系是解本题的关键．
【变式训练9-3】（2020秋•盐城期末）《算法统宗》中记有“李白沽酒”的故事．诗云：今携一壶酒，游春郊外走．逢朋加一倍，入店饮半斗．相逢三处店，饮尽壶中酒．试问能算士：如何知原有？（古代一斗是10升）
大意是：李白在郊外春游时，做出这样一条约定：遇见朋友，先到酒店里将壶里的酒增加一倍，再喝掉其中的5升酒．按照这样的约定，在第3个店里遇到朋友正好喝光了壶中的酒．则李白的酒壶中原有 升酒．
【思路点拨】设壶中原有x升酒，由在第3个店里遇到朋友正好喝光了壶中的酒可得出关于x的一元一次方程，解之即可得出结论．
【规范解答】解：设壶中原有x升酒，
根据题意得：2[2（2x﹣5）﹣5]＝5，
解得：x＝．
答：壶中原有升酒．
故答案为：．
【考点评析】本题考查一元一次方程的应用，理解题意的能力，遇店加一倍，遇到朋友喝一斗，先经过酒店，再碰到朋友，又经过酒店，再碰到朋友，又经过酒店，再碰到朋友．也就是，经过酒店三次，碰到朋友三次酒正好没了壶中酒，可列方程求解．
【变式训练9-4】（2021秋•射阳县校级期末）如图，在长方形ABCD中，AB＝6cm，BC＝8cm，点E是AB上的一点，且AE＝2BE．点P从点C出发，以2cm/s的速度沿点C﹣D﹣A﹣E匀速运动，最终到达点E．设点P运动时间为ts，若三角形PCE的面积为18cm2，则t的值为 或6 ．
【思路点拨】分下列三种情况讨论，如图1，当点P在CD上，即0＜t≤3时，根据三角形的面积公式建立方程求出其解即可；
如图2，当点P在AD上，即3＜t≤7时，由S△PCE＝S四边形AECD﹣S△PCD﹣S△PAE建立方程求出其解即可；
如图3，当点P在AE上，即7＜t≤9时，由S△PCE＝PE•BC＝18建立方程求出其解即可．
【规范解答】解：如图1，当点P在CD上，即0＜t≤3时，
∵四边形ABCD是长方形，
∴AB＝CD＝6cm，AD＝BC＝8cm．
∵CP＝2t（cm），
∴S△PCE＝×2t×8＝18，
∴t＝；
如图2，当点P在AD上，即3＜t≤7时，
∵AE＝2BE，
∴AE＝AB＝4．
∵DP＝2t﹣6，AP＝8﹣（2t﹣6）＝14﹣2t．
∴S△PCE＝×（4+6）×8﹣（2t﹣6）×6﹣（14﹣2t）×4＝18，
解得：t＝6；
当点P在AE上，即7＜t≤9时，
PE＝18﹣2t．
∴S△CPE＝（18﹣2t）×8＝18，
解得：t＝＜7（舍去）．
综上所述，当t＝或6时△APE的面积会等于18．
故答案为：或6．
【考点评析】本题考查了一元一次方程的运用，三角形面积公式的运用，梯形面积公式的运用，动点问题，分类讨论等；解答时要运用分类讨论思想求解，避免漏解．
【变式训练9-5】（2022秋•滨海县月考）我区某中学举办一年一届的科技文化艺术节活动，需搭建一个舞台，请来两名工人．已知甲单独完成需4小时，乙单独完成需6小时．现由乙提前做1小时，剩下的工作由甲、乙两人合做，问再合做几小时可以完成这项工作？
【思路点拨】设再合做x小时可以完成这项工作，根据“甲工作x小时的工作量+乙工作（x+1）小时的工作量＝总工作量”列方程求解．
【规范解答】解：设再合做x小时可以完成这项工作，根据题意，得：
，
解得：x＝2，
答：还需2小时可以完成这项工作．
【考点评析】本题考查一元一次方程的应用（工程问题），理解“工作总量等于工作效率乘以工作时间”的运用，根据条件建立方程是关键．
【变式训练9-6】（2022秋•邳州市期末）如图数轴上有两个点A、B，分别表示的数是﹣2，4．请回答以下问题：
（1）﹣2的绝对值是 2 ，A与B之间距离为 6 ；
（2）若数轴上有点C，使得BC的距离为3个单位长度，则点C表示的数是 7或1 ；
（3）若点P从A点出发，以每秒5个单位长度的速度向右做匀速运动，点Q从B出发，以每秒3个单位长度的速度向右做匀速运动，P，Q同时运动，设运动的时间为t秒：
①当点P运动多少秒时，点P和点Q重合？
②当点P运动多少秒时，P，Q之间的距离为3个单位长度？
【思路点拨】（1）由绝对值概念和两点的距离公式可得答案；
（2）分C在B的左边和右边两种情况；
（3）①由P，Q表示的数相同列方程即可；
②由P，Q之间的距离为3个单位长度列方程可解得答案．
【规范解答】解：（1））﹣2的绝对值是2，A与B之间距离为4﹣（﹣2）＝6，
故答案为：2，6；
（2）点C表示的数是4+3＝7或4﹣3＝1，
故答案为：7或1；
（3）P表示的数为﹣2+5t，Q表示的数为4+3t，
①根据题意得﹣2+5t＝4+3t，
解得t＝3，
∴当点P运动3秒时，点P和点Q重合；
②根据题意得|﹣2+5t﹣（4+3t）|＝3，
解得t＝1.5或t＝4.5，
∴当点P运动1.5秒或4.5秒时，P，Q之间的距离为3个单位长度．
【考点评析】本题考查一元一次方程的应用，解题的关键是读懂题意，能用含t的代数式表示点运动后所表示的数．
【变式训练9-7】（2019秋•赣榆区期末）某校七年级科技兴趣小组计划制作一批飞机模型，如果每人做6个，那么比计划多做了10个，如果每人做5个，那么比计划少做了14个．该兴趣小组共有多少人？计划做多少个飞机模型？
【思路点拨】设该兴趣小组共有x人，由题意表示出计划做的个数为（6x﹣10）或（5x+14），由此联立方程求得人数，进一步求得计划做的个数即可．
【规范解答】解：设该兴趣小组共有x人，由题意得
6x﹣10＝5x+14，
解得：x＝24，
则6x﹣10＝144﹣10＝134．
答：该兴趣小组共有24人，计划做134个飞机模型．
【考点评析】此题考查一元一次方程的实际运用，找出题目蕴含的数量关系：设出人数，表示出做的总个数，利用总个数相等联立方程解决问题
记录
天平左边
天平右边
天平状态
乒乓球总质量
一次性纸杯的总质量
记录一
6个乒乓球，1个10克的砝码
14个一次性纸杯
平衡
6x
6x+10
记录二
4个乒乓球
1个一次性纸杯
1个10克的砝码
平衡
4x
4x﹣10
x
﹣2
0
2
ax﹣b
﹣6
﹣3
0
品名
单价（元/棵）
栽树劳务费（元/棵）
成活率
A
15
3
96%
B
20
4
92%