苏科版数学八上期末专题训练 轴对称30道压轴题训练（2份，原卷版+解析版）

这是一份苏科版数学八上期末专题训练 轴对称30道压轴题训练（2份，原卷版+解析版），文件包含苏科版数学八上期末专题训练轴对称30道压轴题训练原卷版doc、苏科版数学八上期末专题训练轴对称30道压轴题训练解析版doc等2份试卷配套教学资源，其中试卷共79页， 欢迎下载使用。
轴对称30道压轴题训练
【重难点训练】
一、单选题
1．如图，在△ABC中，∠B、∠C的平分线交于点F，过点F作DE∥BC交AB于点D，交AC于点E，下列结论：①△BDF，△ADE都是等腰三角形；②DE＝BD＋CE；③△ADE的周长等于AB＋AC；④BF＝CF；⑤若∠A＝80°，则∠BFC＝130°，其中正确的有（ ）
A．2个B．3个C．4个D．5个
2．如图，E是BC延长线上的一点，AD∥BC，BD，CD，AP，DP分别平分∠ABC，∠ACE，∠BAC，∠BDC，则∠P的度数为（ ）
A．30°B．42°C．45°D．50°
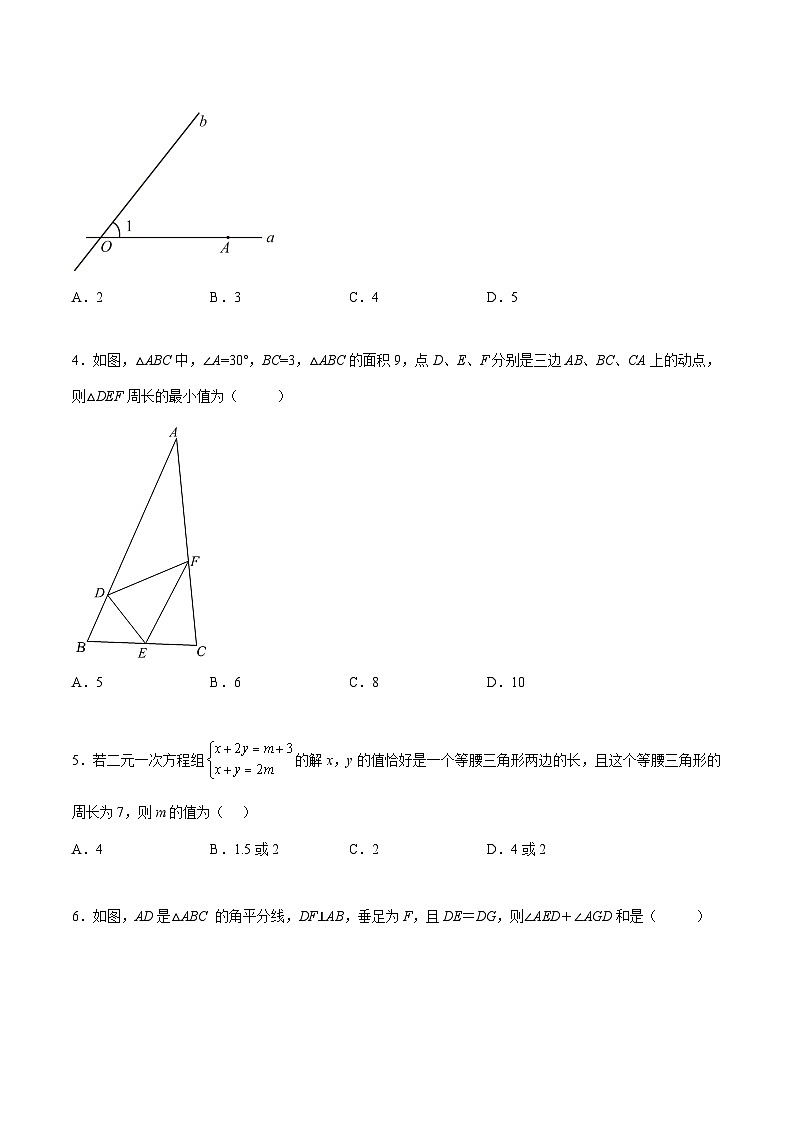
3．如图，直线，相交于点，，点在直线上，直线上存在点，使以点，，为顶点的三角形是等腰三角形，则点的个数是（ ）
A．2B．3C．4D．5
4．如图，△ABC中，∠A=30°，BC=3，△ABC的面积9，点D、E、F分别是三边AB、BC、CA上的动点，则△DEF周长的最小值为（ ）
A．5B．6C．8D．10
5．若二元一次方程组的解x，y的值恰好是一个等腰三角形两边的长，且这个等腰三角形的周长为7，则m的值为（ ）
A．4B．1.5或2C．2D．4或2
6．如图，AD是△ABC 的角平分线，DF⊥AB，垂足为F，且DE＝DG，则∠AED＋∠AGD和是（ ）
A．180°B．200°C．210°D．240°
7．如图，长方形ABKL，延CD第一次翻折，第二次延ED翻折，第三次延CD翻折，这样继续下去，当第五次翻折时，点A和点B都落在∠CDE＝内部（不包含边界），则的取值值范围是（ ）
A．B．C．D．
8．如图，△ABC中，∠CAB＝∠CBA＝48°，点O为△ABC内一点，∠OAB＝12°，∠OBC＝18°，则∠ACO+∠AOB＝（ ）
A．190°B．195°C．200°D．210°
9．如图，在中，，过点作于点，点是上一点，将沿着翻折得到，连接，若，，三点恰好在同一条直线上，则的度数是（ ）
A．B．C．D．
10．如图，在中，，以AC为底边向外作等腰，，在CD上截取，连接BE．若，则的度数为（ ）
A．10°B．15°C．20°D．30°
二、填空题
11．如图，在中，，的平分线交于点，的平分线交于点，点在边上，，连接，则________．
12．如图，中，、的角平分线、交于点，延长、，，，则下列结论中正确的是 ___．（填序号）①平分；②；③；④．
13．如图，在等腰中，，于点，以为边作等边三角形，与在直线的异侧，直线交直线于点，连接交于点．若，，则______．
14．如图，在△ABC中，AB=AC，∠BAC=100°，BD平分∠ABC，且BD=AB，连接AD、DC．则∠BDC的度数为__________°．
15．如图，等边中，，M是高所在直线上的一个动点，连接，将线段点B逆时针旋转60°得到，连接．在点M运动过程中，线段长度的最小值是___________．
16．如图，M，N是∠AOB的边OA上的两个点(OM＜ON)，∠AOB＝30°，OM＝a，MN＝4．若边OB上有且只有1个点P，满足△PMN是等腰三角形，则a的取值范围是__________．
17．如图，已知∠MON=30点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4，…均为等边三角形，若OA1=1，则△A2021B2021A2022的边长为______．
18．如图，△ABD与△ACE都是等边三角形，且AB≠AC，下列结论：①BE=CD；②∠BOD=60°；③∠BDO=∠CEO；④若∠BAC=90°，DA∥BC，则BC⊥EC．其中正确的是 _____（填序号）．
19．如图，△ABC中，∠B＝30°，∠ACB＝90°，AB＝2，D在BC上，将线段AD绕点A逆时针旋转60°得AP，则CP的最小值为_____．
20．如图，在四边形ABCD中，，E、F分别是AD、BC上的点，将四边形CDEF沿直线EF翻折，得到四边形C′D′EF．C′F交AD于点G，若是等腰三角形，则______．
三、解答题
21．如图，在Rt△ABC中，，，F为直线AB上一点，连接FC．作于点D，连接AD，过点A作交BD于点E．
(1)如图1，求证：AD=AE
(2)如图2，若点H是BD中点，连接AH、CE，求证：
(3)如图3，当点F运动到线段AB上且不与A、B重合时，连接CE，过点A作交BD于点H，猜想CE与AH之间的数量关系并证明．
22．知Rt△ABC和Rt△ADE，AB＝AC，AD＝AE．连接BD、CE，过点A作AH⊥CE于点H，反向延长线段AH交BD于点F．
(1)如图1，当AB＝AD时
①请直接写出BF与DF的数量关系：BF_________DF（填“＞”、“＜”、“＝”）
②求证：CE＝2AF
(2)如图2，当AB≠AD时，上述①②结论是否仍然成立？若成立，请证明；若不成立，请说明理由．
23．探究与应用
(1)【操作发现】如图1，为等边三角形，点D为边上的一点，，将线段绕点C顺时针旋转得到线段，连接、，请直接写出下列结果：
①的度数为___________；
②与之间的数量关系为______________；
(2)【类比探究】如图2，为等腰直角三角形，，点D为边上的一点，，将线段绕点C顺时针旋转得到线段，连接、．
则线段，，之间有什么数量关系？请说明理由；
(3)【拓展应用】如图3，是一个三角形的余料，小张同学量得，，他在边上取了D、E两点，并量得、，这样、将分成三个小三角形，则________________．
24．等边ΔABC的边BC上有一点E，点D在直线AB上，以DE为边作等边ΔDEF；
(1)如图①当D与A重合时，在DE的左侧作等边ΔDEF，连接BF，求证：BF∥AC；
(2)如图②当D在射线BA上时，在DE的左侧作等边ΔDEF，请直接写出：DA、BF、EC这三条线段之间的数量关系；
(3)如图③当D是AB中点时，在DE的右侧作等边ΔDEF，连接CD，请直接写出点E在线段BC上运动时，∠CFD与∠CDE之间的关系．
25．已知△ABC是等边三角形，点D在射线BC上（与点B，C不重合），点D关于直线AC的对称点为点E，连接AD，AE，CE，DE．
(1)如图1，当点D为线段BC的中点时，求证：△ADE是等边三角形；
(2)当点D在线段BC的延长线上时，连接BE，F为线段BE的中点，连接CF．根据题意在图2中补全图形，用等式表示线段AD与CF的数量关系，并证明．
26．（1）【探究发现】如图①，等腰△ACB，∠ACB =90°，D为 AB 的中点，∠MDN=90°，将∠MDN绕点D旋转，旋转过程中，∠MDN的两边分别与线段 AC、线段 BC交于点 E、F（点 F与点 B、C不重合），写出线段 CF、CE、BC 之间的数量关系，并证明你的结论；
（2）【类比应用】如图②，等腰△ACB，∠ACB=120°，D 为 AB 的中点，∠MDN=60°，将∠MDN 绕点 D 旋转，旋转过程中，∠MDN 的两边分别与线段 AC、线段 BC 交于点 E、F（点 F 与点 B、C 不重合），直接写出线段 CF、CE、 BC 之间的数量关系为______；
（3）【拓展延伸】如图③，在四边形 ABCD 中，AC 平分∠BCD，∠BCD=120°，DAB=60°，过点 A 作 AE⊥AC， 交 CB 的延长线于点 E，若 CB=6，DC=2，则 BE 的长为 ．
27．（1）如图1，在中，，，是边上的中线，延长到点使，连接，把，，集中在中，利用三角形三边关系可得的取值范围是______；
（2）如图2，在中，是边上的中线，点，分别在，上，且，求证：；
（3）如图3，在四边形中，为钝角，为锐角，，，点，分别在，上，且，连接，试探索线段，，之间的数量关系，并加以证明．
28．如图1，已知等边ABC边长为4cm，点P、Q分别是边AB、BC上的动点，点P、Q分别从点A、B同时出发，且它们的速度都为1cm/s．连接AQ、CP交于点M．
(1)求证：ABQ≌CAP；
(2)在整个运动过种中，∠CMQ会发生变化吗？若变化，则说明理由；若不变，求出它的度数．
(3)连接PQ，何时PBQ是直角三角形？
(4)如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交于点M，求∠CMQ的度数．
29．【阅读】
通过构造恰当的图形，可以对线段长度大小进行比较，直观地得到线段之间的数量关系，这是“数形结合”思想的典型应用．
【理解】
（1）如图1，，AC平分，求证：．
【拓展】
（2）如图2，其他条件不变，将图1中的绕点C逆时针旋转，CD交MA的延长线于点D，CB交射线AN于点B，写出线段AD，AB，AC之间的数量关系，并就图2的情形说明理由．
【应用】
（3）如图3，为等边三角形，，P为BC边的中点，，将绕点P转动使射线PM交直线AC于点M，射线PN交直线AB于点N，当时，请直接写出AN的长．
30．如果一个三角形能用一条直线将其分割出两个等腰三角形，那么我们称这个三角形为“活三角形”，这条直线称为该“活三角形”的“生命线”．
(1)小明在研究“活三角形”问题时（如图），他发现，在△ABC中，若∠BAC＝3∠C时，这个△ABC一定是“活三角形”．点D在BC边上一点，连接AD，他猜测：当∠DAC＝∠C时，AD就是这个三角形的“生命线”，请你帮他说明AD是△ABC的“生命线”的理由；
(2)如小明研究结果可以总结为：
，该三角形是一个“活三角形”．请通过自己操作研究，并根据上述结论，总结“活三角形”的其他特征；（注意从三角形边、角特征及相互间关系总结）
(3)如果一个等腰三角形是一个“活三角形”那么它的顶角大小为 度．（直接写出结果即可）