苏科版数学八上期末专题训练 轴对称常考折叠问题（32道）（2份，原卷版+解析版）

这是一份苏科版数学八上期末专题训练 轴对称常考折叠问题（32道）（2份，原卷版+解析版），文件包含苏科版数学八上期末专题训练轴对称常考折叠问题32道原卷版doc、苏科版数学八上期末专题训练轴对称常考折叠问题32道解析版doc等2份试卷配套教学资源，其中试卷共69页， 欢迎下载使用。
知识要点一 ： 折叠（对折）的定义
一条直线把一个平面图形分成两个全等的图形,其中的一个图形沿着这条直线翻折到另一个图形上面,则两部分完全重合,这个过程就叫做对折.
知识要点二： 折叠（对折）的特点
折叠问题实际上就是对称变换；
折叠是一种对称变换，属于轴对称，对称轴（折㡾所在直线）是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等；
教学初，为使学生直观感悟，可以进行一些实际操作，以便于学生形成直观感受，利于问题的解决。
知识要点三： 折叠（对折）的基本图形及图形特点
折叠图形的基本背景图形有：三角形、四边形、梯形等，解决这些问题的基本方法是精确找出折叠前后相等边与角，以及结合图形的性质把边角的关系联系起来，同时结合方程思想、数形结合等数学思想进行解题。
折叠特点：有折叠----就有重合----就有全等-----对应线段相等、对应角相等，运用勾股定理、等面积法结合图形特点进行解题。
【典例】如图1，将长方形ABEF的一角向长方形内部折叠，使角的顶点A落在点处，OC为折痕，则OC平分．

(1)若∠AOC＝25°，求 的度数；
(2)若点D在线段BE上，角OBD沿着折痕OD折叠落在点处，且点在长方形内．
①如果点刚好在线段上，如图2所示，求∠COD的度数；
②如果点不在线段上，且＝40°，求∠AOC+∠BOD的度数．
【答案】(1)
(2)① ；②70°或110°
【分析】
（1）根据折叠的性质，可得 ，即可求解；
（2）①根据折叠的性质，可得 ，从而得到，即可求解；
②分两种情况：当 在右侧时，当 在左侧时，即可求解．
(1)解：∵OC平分．∠AOC＝25°，
∴ ，
∴；
(2)解：①根据题意得： ，
∴ ；
②如图，当 在右侧时，
根据题意得： ，
∵＝40°，
∴ ，
∴ ；
如图，当 在左侧时，
根据题意得： ，
∵＝40°，
∴，
∴ ；
综上所述，∠AOC+∠BOD的度数70°或110°．
【点拨】本题主要考查了折叠的性质，有关角平分线的计算，熟练掌握图形折叠前后对应角相等，对应线段相等是解题的关键．
【32道重难点题型】
1．（2022·江苏·泰州市第二中学附属初中七年级期末）如图，把沿EF翻折，叠合后的图形如图，若，，则的度数是（ ）
A．15°B．20°C．25°D．35°
【答案】C
【解析】
【分析】
先根据折叠的性质得到∠BEF=，∠CFE=，再根据邻补角的定义得到180°-∠AEF=∠1+∠AEF，180°-∠AFE=∠2+∠AFE，则可计算出 ∠AEF=42.5°，再根据三角形内角和定理计算出∠AFE=77.5°，然后把∠AFE=77.5°代入180°-∠AFE=∠2+∠AFE即可得到∠2的度数．
【详解】
解：如图，∵△ABC沿EF翻折，
∴∠BEF=，∠CFE=，
∴180°-∠AEF=∠1+∠AEF，180°-∠AFE=∠2+∠AFE，
∵∠1=95°，
∴∠AEF=（180°-95°）=42.5°，
∵∠A+∠AEF+∠AFE=180°，
∴∠AFE=180°-60°-42.5°=77.5°，
∴，
∴∠2=25°．
故选C．
【点睛】
本题考查了折叠的性质：翻折变换（折叠问题）实质上就是轴对称变换；折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．同时考查了三角形的内角和定理的应用．
2．（2022·江苏·八年级专题练习）将一张纸如图所示折叠后压平，点F在线段BC上，EF、GF为两条折痕，若∠EFG＝α，则∠B'FC'的度数是（ ）
A．α﹣45°B．2α﹣90°C．90°﹣αD．180°﹣2α
【答案】D
【解析】
【分析】
由折叠的性质可知∠EFB＝∠EFB′，∠CFG＝∠C′FG，因为∠EFG＝α，得到∠EFB+∠CFG=180°﹣α，所以∠EFB′+∠C′FG＝180°﹣α，根据∠B'FC'＝∠EFB+∠EFB′+∠CFG+∠C′FG﹣180°即可求解；
【详解】
解：由折叠的性质可知，∠EFB＝∠EFB′，∠CFG＝∠C′FG，
∵∠EFG＝α，
∴∠EFB+∠CFG＝180°﹣∠EFG＝180°﹣α，
∴∠EFB′+∠C′FG＝180°﹣α，
∴∠B'FC'＝∠EFB+∠EFB′+∠CFG+∠C′FG﹣180°，
＝（180°﹣α）+（180°﹣α）﹣180°，
＝180°﹣2α，
故选：D．
【点睛】
考查折叠的性质，角度的和差运算，根据折叠得到相等的角是关键．
3．（2022·浙江杭州·七年级期末）图，，，，点为线段上一点，将线段沿折叠，点的对应点落在四边形外侧，连接，若，，则为( )
A．B．
C．D．
【答案】D
【解析】
【分析】
设，先根据平行线的性质可得，从而可得，再根据折叠的性质可得，从而可得，然后根据平行线的性质可得，从而可得，由此即可得．
【详解】
解：设，
，
，
，
，
由折叠的性质得：，
，
，
，
，
解得，
即，
故选：D．
【点睛】
本题考查了平行线的性质、折叠的性质等知识点，熟练掌握平行线的性质是解题关键．
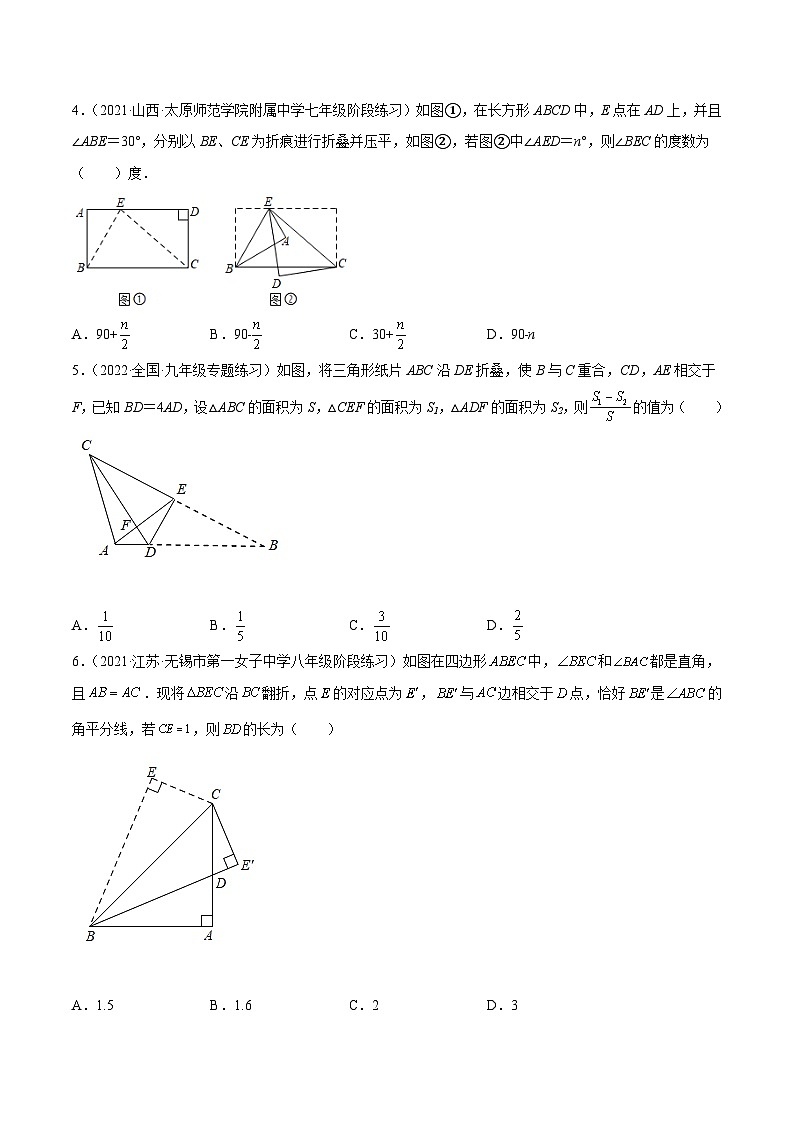
4．（2021·山西·太原师范学院附属中学七年级阶段练习）如图①，在长方形ABCD中，E点在AD上，并且∠ABE＝30°，分别以BE、CE为折痕进行折叠并压平，如图②，若图②中∠AED＝n°，则∠BEC的度数为（ ）度．
A．90+B．90﹣C．30+D．90﹣n
【答案】B
【解析】
【分析】
根据∠A=∠A′=90°，∠ABE＝30°，得出∠1=∠AEB=60°，根据平角定义可得∠DED′=180°-∠1-（∠AEB-∠DEA）=60°+n°，可得∠2=∠DED′=（n+30）°，根据平角定义可得∠BCE=180°-∠1-∠2=（90-）°即可．
【详解】
解：如图，
∵∠A=∠A′=90°，∠ABE＝30°，
∴∠1=∠AEB=90°-∠ABE=60°，
∴∠DED′=180°-∠1-（∠AEB-∠DEA）=180°-60°-60°+n°=60°+n°，
∴∠2=∠DED′=（n+30）°，
∴∠BCE=180°-∠1-∠2=180°-60°-（）°=（90-）°．
故选B．
【点睛】
此题考查了翻折变换的性质、矩形的性质以及直角三角形的性质；平角定义，注意数形结合思想的应用．
5．（2022·全国·九年级专题练习）如图，将三角形纸片ABC沿DE折叠，使B与C重合，CD，AE相交于F，已知BD＝4AD，设△ABC的面积为S，△CEF的面积为S1，△ADF的面积为S2，则的值为（ ）
A．B．C．D．
【答案】C
【解析】
【分析】
由折叠可知 ，进而得到，过E作EH⊥AB于H，CM垂直AB交BA的延长线于M，由BD＝4AD得到，进而得到，再利用三角形面积公式推出，即可求解．
【详解】
解：由折叠可知 ，
∴ ，
∴ ，
∴①，
过E作EH⊥AB于H，CM垂直AB交BA的延长线于M，
∴ ， ，
∵BD＝4AD，
∴ ，
∴ ②，
①－②得： ，
∵CM⊥AB，
∴ ，
，
∴ ，
∴ ，
∴ ，
∴ ,
故选：C．
【点睛】
本题考查折叠的性质、全等三角形的性质及三角形面积，解题关键是正确作出辅助线．
6．（2021·江苏·无锡市第一女子中学八年级阶段练习）如图在四边形中，和都是直角，且．现将沿翻折，点的对应点为，与边相交于点，恰好是的角平分线，若，则的长为（ ）
A．1.5B．1.6C．2D．3
【答案】C
【解析】
【分析】
延长CE′和BA相交于点F，根据翻折的性质可以证明△BE′C≌△BE′F，可得CF=2，再证明△FCA≌△DBA，可得BD=CF=2．
【详解】
解：如图，延长CE′和BA相交于点F，
由翻折可知：
∠BE'C=∠E=90°，CE'=CE=1，
∵BE'是∠ABC的角平分线，
∴∠CBE'=∠FBE'，
∵BE′=BE′，
∴△BE'C≅△BE'F(ASA)，
∴E'F=CE'=1，
∴CF=2，
∵∠FCA+∠F=90°，∠DBA+∠F=90°，
∴∠FCA=∠DBA，
∵∠FAC=∠DAB=90°，AB=AC，
∴△FCA≅△DBA(ASA)，
∴BD=CF=2．
故选：C．
【点睛】
此题考查了折叠的性质、全等三角形的判定与性质．熟练掌握全等三角形的判定与性质和折叠的性质是解决问题的关键．
7．（2020·四川·德阳五中八年级阶段练习）如图，△ABE、△ADC是△ABC分别沿着AB、AC边翻折180°形成的．若∠BAC：∠ABC：∠ACB＝28：5：3，则∠EFC的度数为（ ）
A．75°B．80°C．95°D．100°
【答案】B
【解析】
【分析】
由题意设∠BAC＝28x，∠ABC＝5x，∠ACB＝3x，利用三角形的内角和定理可求解x值，即可求解∠BAC＝140°，∠ABC＝25°，∠ACB＝15°，再由折叠的性质可求得∠FBC，∠FCB的度数，根据三角形外角的性质可求解．
【详解】
解：∵∠BAC：∠ABC：∠ACB＝28：5：3，
∴设∠BAC＝28x，∠ABC＝5x，∠ACB＝3x，
∴28x+5x+3x＝180°，
解得x＝5，
∴∠BAC＝140°，∠ABC＝25°，∠ACB＝15°，
由折叠可知：∠EBA＝∠ABC＝25°，∠ACD＝∠ACB＝15°，
∴∠FBC＝50°，∠FCB＝30°，
∴∠EFC＝∠FBC+∠FCB＝50°+30°＝80°，
故选：B．
【点睛】
本题考查了折叠的性质：折叠前后两图形全等，即对应角相等，对应线段相等．也考查了三角形的内角和定理以及周角的定义．
8．（2022·山东青岛·模拟预测）如图，将长方形纸片ABCD，沿折痕MN折叠，B分别落在A1，B1的位置，A1B1交AD于点E，若∠BNM＝65°，以下结论：①∠B1NC＝50°；②∠A1ME＝50°；③A1M∥B1N；④∠DEB1＝40°．正确的个数有（ ）
A．1个B．2个C．3个D．4个
【答案】D
【解析】
【分析】
由折叠的性质可得∠B1NM=∠BNM＝65°，再根据平角的定义可得∠B1NC，故可判断①；根据平行线的性质可得∠AMN＝115°，由折叠得∠A1MN＝115°，依据∠AMN+∠A1MN-180°=50°可判断②；由∠B1NM+∠A1MN=180°可判断③；根据直角三角形的两个锐角互余可得④．
【详解】
解：在长方形纸片ABCD中，∠A=90°，AD∥BC，
∴∠BNM+∠AMN=180°，
∵∠BNM＝65°，
∴∠AMN＝115°，
由折叠的性质可得：∠B1NM=∠BNM＝65°，∠AMN＝∠A1MN＝115°，
∵∠BNM+∠B1NM+∠B1NC=180°，
∴∠B1NC＝50°；故①正确；
∵∠AMN＝∠A1MN＝115°，
∴∠A1ME＝∠AMN+∠A1MN-180°=50°，故②正确；
∵∠A1MN＝115°，∠B1NM＝65°，
∴∠B1NM+∠A1MN=180°，
∴A1M∥B1N，故③正确；
∵∠A1=∠A=90°，
∴∠A1ME+∠A1EM=90°，
∵∠A1ME=50°，
∴∠DEB1=∠A1EM＝40°，故④正确；
故选D．
【点睛】
本题主要考查折叠的性质、平行线的性质与判定及直角三角形的两个锐角互余，熟练掌握折叠的性质、平行线的性质与判定及直角三角形的两个锐角互余是解题的关键．
9．（2021·浙江·七年级期中）如图，将一长方形纸片沿着折叠，已知，，交于点过点作，交线段于点．若，则的度数（ ）
A．B．C．D．无法确定
【答案】B
【解析】
【分析】
根据平行线的性质得到和角平分线的定义证明GH平分∠AGE，由折叠的性质得到∠EFG=∠1，根据平行线的性质和平角的定义即可得到结论．
【详解】
解：∵GH∥EF，
∴∠AGH=∠AFE，∠HGE=∠GEF，
∵CE∥DF，
∴∠1=∠GEF，
∵∠1=∠GFE，
∴∠GFE=∠GEF，
∴∠AGH=∠EGH，
∴GH平分∠AGE，
∵将一长方形纸片ABCD沿着EF折叠，
∴∠EFG=∠1，
∵∠DFG=46°，
∴∠EFG=（180°-46°）=67°，
∵GH∥EF，
∴∠AGH=∠AFE=67°，
∵GH平分∠AGE，
∴∠HGE=67°．
故选：B
【点睛】
本题考查了长方形的性质，平行线的性质，折叠的性质，正确的识别图形是解题的关键．
10．（2021·四川省绵阳南山中学双语学校八年级期中）如图，在中，，点D是BC上一点，BD的垂直平分线交AB于点E，将沿AD折叠，点C恰好与点E重合，则等于（ ）
A．19°B．20°C．24°D．25°
【答案】B
【解析】
【分析】
根据垂直平分线和等腰三角形性质，得；根据三角形外角性质，得；根据轴对称的性质，得，，；根据补角的性质计算得，根据三角形内角和的性质列一元一次方程并求解，即可得到答案．
【详解】
∵BD的垂直平分线交AB于点E，
∴
∴
∴
∵将沿AD折叠，点C恰好与点E重合，
∴，，
∵
∴
∵
∴
∴
故选：B．
【点睛】
本题考查了轴对称、三角形内角和、三角形外角、补角、一元一次方程的知识；解题的关键是熟练掌握轴对称、三角形内角和、三角形外角的性质，从而完成求解．
11．（2021·上海市民办新黄浦实验学校七年级期中）如图所示，正方形ABCD的边长为a，正方形ABCD的面积记作，取各边中点，顺次连接得到的正方形面积记作，以此类推，则可用含a的代数式表示为（ ）
A．B．C．D．
【答案】C
【解析】
【分析】
根据折叠的性质求得、的面积，观察规律，即可求解．
【详解】
解：由题意可知：正方形ABCD的面积
由题意可得：分别为各边的中点，
将正方形沿、进行折叠，可得与重合，与重合，
可以得到、、、
又∵
∴
同理可得，…
故选C
【点睛】
此题考查了图形类规律的探索问题，解题的关键是求出前面图形的面积，得出规律．
12．（2021·山东泰安·七年级期中）如图，将沿翻折，使其顶点均落在点处，若，则的度数为（ ）
A．B．C．D．
【答案】B
【解析】
【分析】
由折叠的性质可得，，可得，由三角形内角和定理可得，利用三角形外角定理得出，建立方程，即可求的度数．
【详解】
解：延长交于点，
∵将沿，翻折，顶点，均落在点处，
∴，，
∴，
∵，
∴ ，
由三角形外角定理可知：，，
∴
即：，
∴ ，
∴，
故选：．
【点睛】
本题考查了折叠的性质，三角形内角和定理，外角定理，熟练运用三角形内角和定理是本题的关键．
13．（2021·河南省淮滨县第一中学模拟预测）如图，△ABC中，∠A＝20°，沿BE将此三角形对折，又沿BA′再一次对折，点C落在BE上的C′处，此时∠C′DB＝74°，则原三角形的∠C的度数为（ ）
A．27°B．59°C．69°D．79°
【答案】D
【解析】
【分析】
由折叠的性质得∠1＝∠2，∠2＝∠3，∠CDB＝∠C′DB＝74°，则∠1＝∠2＝∠3，即∠ABC＝3∠3，由三角形内角和定理得∠3＋∠C＝106°，在△ABC中，由三角形内角和定理得∠A＋∠ABC＋∠C＝180°，得出∠3＝27°，即可得出结果．
【详解】
解：如图所示：
∵△ABC沿BE将此三角形对折，又沿BA′再一次对折，点C落在BE上的C′处，
∴∠1＝∠2，∠2＝∠3，∠CDB＝∠C′DB＝74°，
∴∠1＝∠2＝∠3，
∴∠ABC＝3∠3，
在△BCD中，∠3＋∠C＋∠CDB＝180°，
∴∠3＋∠C＝180°−74°＝106°，
在△ABC中，
∵∠A＋∠ABC＋∠C＝180°，
∴20°＋2∠3＋106°＝180°，
∴∠3＝27°，
∴∠C＝106°-∠3＝79°．
故选：D．
【点睛】
本题考查了翻折变换的性质、三角形内角和定理；熟练掌握翻折变换的性质和三角形内角和定理，并能进行推理计算是解决问题的关键．
14．（2021·安徽·铜陵市第十五中学七年级期中）已知，点分别在直线上，点在之间且在的左侧．若将射线沿折叠，射线沿折叠，折叠后的两条射线互相垂直，则的度数为（ ）
A．B．C．或D．或
【答案】C
【解析】
【分析】
根据题意画出示意图，延长FP交AB于点Q，根据折叠的性质和四边形的内角和进行分析解答即可．
【详解】
解：根据题意，延长FP交AB于点Q，可画图如下：
∵
∴
∵将射线沿折叠，射线沿折叠，
∴，
∵，
如第一个图所示，在四边形FPEM中，，
得：，
∴．
如第二个图所示，在四边形FPEM中，，
得：，
∴．
故选：C．
【点睛】
本题考查的知识点是平行线的性质、折叠的性质、三角形的外角、四边形的内角和等知识．关键是利用平行线的性质以及四边形内角和进行解答．
15．（广东·肇庆市地质中学八年级阶段练习）如图，在△ABC中，AB=AC，∠BAC=54°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC的度数为（ ）
A．120°B．108°C．110°D．102°
【答案】B
【解析】
【分析】
连接OB、OC，根据角平分线的定义求出∠BAO，根据等腰三角形两底角相等求出∠ABC，再根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB，根据等边对等角可得∠ABO=∠BAO，再求出∠OBC，然后判断出点O是△ABC的外心，根据三角形外心的性质可得OB=OC，再根据等边对等角求出∠OCB=∠OBC，根据翻折的性质可得OE=CE，然后根据等边对等角求出∠COE，再利用三角形的内角和定理列式计算即可得解．
【详解】
解：如图，连接OB、OC，
∵∠BAC=54°，AO为∠BAC的平分线，
∴∠BAO=∠BAC=×54°=27°，
又∵AB=AC，
∴∠ABC=（180°∠BAC）=（180°54°）=63°，
∵DO是AB的垂直平分线，
∴OA=OB，
∴∠ABO=∠BAO=27°，
∴∠OBC=∠ABC-∠ABO=63°27°=36°，
∵AO为∠BAC的平分线，AB=AC，
∴△AOB≌△AOC（SAS），
∴OB=OC，
∴点O在BC的垂直平分线上，
又∵DO是AB的垂直平分线，
∴点O是△ABC的外心，
∴∠OCB=∠OBC=36°，
∵将∠ACB沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，
∴OE=CE，
∴∠COE=∠OCB=36°，
在△OCE中，∠OEC=180°∠COE∠OCB=180°36°36°=108°；
故选：B.
【点睛】
本题考查了翻折变换的性质，线段垂直平分线上的点到线段两端点的距离相等的性质，等腰三角形三线合一的性质，等边对等角的性质，综合性较强，难度较大，作辅助线，构造出等腰三角形是解题的关键．
16．（2022·甘肃兰州·七年级期末）如图，三角形纸片ABC中，∠A=65°，∠B=75°，将纸片的一角折叠，使点C落在△ABC内，若∠1=20°，则∠2的度数为______ 度．
【答案】60
【解析】
【分析】
如图延长AE、BF交于点，连接．利用三角形的外角的性质证明∠1+∠2=，求出即可解决问题．
【详解】
解：如图延长AE、BF交于点，连接． ∠A=65°，∠B=75°，
在中，，
∵∠ECF==40°，
∴∠1+∠2=，
∵∠1=20°，
∴∠2=60°，
故答案为：60．
【点睛】
本题考查翻折变换、三角形的内角和定理、三角形的外角等知识，解题的关键是灵活运用所学知识解决问题，也可以记住基本结论∠1+∠2=解决问题．
17．（2022·重庆万州·七年级期末）如图，中，，D、E是AC边上的点，把沿BD对折得到，再把沿BE对折得到，若恰好落在BD上，且此时，则______．
【答案】60°##60度
【解析】
【分析】
由折叠可得，∠BEC=，∠ABD=∠DBE=∠EBC，依据∠BEC是△ABE的外角，即可得到∠ABE=∠BEC-∠A=40°，进而得到∠ABC为60°．
【详解】
解：由折叠可得，∠BEC=，∠ABD=∠DBE=∠EBC，
∵∠BEC是△ABE的外角，
∴∠ABE=∠BEC-∠A=80°-40°=40°，
∴∠ABD=∠DBE=20°，
∴∠ABC=3×20°=60°，
故答案为：60°．
【点睛】
此题主要考查的是图形的折叠变换及三角形外角的性质，能够根据折叠的性质发现∠ABD=∠DBE=∠EBC是解答此题的关键．
18．（2022·河南信阳·七年级期中）如图1，∠DEF＝25°，将长方形纸片ABCD沿直线EF折叠成图2，再沿折痕GF折叠成图3，则∠CFE的度数为______．
【答案】105°
【解析】
【分析】
由矩形的性质可知AD// BC，由此可得出∠BFE=∠DEF=25°，再根据翻折的性质可知翻折一次减少一个∠BFE的度数，由此即可算出∠CFE度数．
【详解】
解：∵四边形A BCD为长方形，
∴AD//BC，
∴∠BFE=∠DEF=25° ．
由翻折的性质可知：
图2中，∠EFC=180°-∠BFE=155°，∠BFC=∠EFC-∠BFE= 130*，
图3中，∠CFE=∠BFC-∠BFE= 105° ．
故答案为： 105°．
【点睛】
本题考查了平行线的性质，翻折变换以及矩形的性质，根据翻折变换找出相等的边角关系是关键．
19．（2022·福建省厦门第六中学七年级期中）如图，直角梯形纸片对边，是直角，将纸片沿着EF折叠，DF的对应边交AB于点G，FH平分交AC于点H．则结论：①；②；③；④若，则．其中结论正确的有_______（填序号）
【答案】①③④
【解析】
【分析】
由平行线的性质可得∠GEF=∠EFD，∠AGF=∠GFD，由折叠的性质可得∠GFE=∠EFD，可得∠AGF=2∠GFE，∠GEF=∠GFE=∠EFD，可判断①和②；由角平分线的性质和平角的性质可得，由余角的性质可得∠CHF=∠GFE，可判断③；由折叠的性质可求∠BEF的值，可求∠GFE=∠GEF=55°，可判断④；即可求解．
【详解】
解：∵，
∴∠GEF=∠EFD，∠AGF=∠GFD，
∵将纸片沿着EF折叠，DF的对应边交AB于点G，
∴∠GFE=∠EFD，
∴∠AGF=2∠GFE，故①正确；
∵∠GEF=∠GFE=∠EFD，
∴GE=GF，
∵无法证明△GEF是等边三角形，
∴GE≠EF，
∴∠EGF≠∠GFE；故②错误；
∵FH平分，
∴，
∵，
∴，
又∵，
∴，故③正确；
∵将纸片沿着EF折叠，DF的对应边D'F交AB于点G，
∴，
∴∠BEF==125°，
∴∠GEF=55°=∠GFE，故④正确；
综上分析可知，正确的结论有①③④．
故答案为：①③④．
【点睛】
本题主要考查了翻折变换，梯形的性质，平行线的性质，掌握折叠的性质是本题的关键．
20．（2021·山东潍坊·八年级期中）如图，在中，，，，将沿折叠，使得点恰好落在边上的点处，折痕为，若点为上一动点，则的周长最小值为___________．
【答案】7
【解析】
【分析】
根据折叠可知B和E关于AD对称，由对称的性质得出当F和D重合时，EF+FC的值最小，即此时的周长最小，最小值是EF+FC+EC=BD+CD+EC，先求出EC长，代入求出即可．
【详解】
解：连接BF
由题可知B和E关于AD对称，AB=AE=4，
∴BF=FE
△CFE的周长为：EF+FC+EC=BF+CD+EC
当F和D重合时，BF+CD= BC
∵两点之间线段最短
∴此时BF+CD的值最小，
即此时△CFE的周长最小，
最小值是EF+FC+EC=BD+CD+EC=BC+EC，
∵EC=AC-AE=6-4=2，
∴的周长最小值为：BC+EC=5+2=7，
故答案为：7．
【点睛】
本题考查了折叠性质，轴对称−最短路线问题，关键是确定点F的位置．
21．（2021·浙江杭州·七年级期末）如图，将一条两边互相平行的纸带折叠，折痕为DE，平分线所在直线与平分线所在直线相交于点F，若，则的度数为_________．
【答案】36°
【解析】
【分析】
运用平行线的性质、图形翻折的特点，结合△FBD的内角和等于180°，从而列出关系式，进而得出结论．
【详解】
解：如图．
令，则．
由题意得：，．
，．
．
．
又直线是的角平分线．
．
．
又直线是的角平分线所在直线．
．
．
又．
．
．
，
故答案为：36°．
【点睛】
本题主要考查平行线的性质、图形翻折的特点，结合三角形内角和的性质，运用化归的思想破解该题．
22．（2022·湖北黄石·七年级阶段练习）如图，将长方形纸片沿折痕EF折叠，点，的对应点分别为点，，交于点，再把三角形沿折叠，点的对应点为点，若，则的大小是______．
【答案】138°
【解析】
【分析】
过点D′作D′M//AD，先由折叠的性质得∠D′GB=∠C′GF=∠HGF，∠HFG=∠C′FG，由已知条件可得出∠HGC的度数，再根据对称性可得∠D′GB=∠C′GF的度数，再根据平行线的性质，可得∠MD′G的度数，即可算出∠ED′M的度数，再由平行线的性质即可得出∠AED′的度数，再由平角的性质即可得出答案．
【详解】
解：过点D′作D′M//AD，如图，
由折叠的性质得∠D′GB=∠C′GF=∠HGF，∠HFG=∠C′FG，
∵∠D'GH=104°，∠HGC′+∠D'GH=180°，
∴∠HGC′=180°-104°=76°，
∴∠D′GB=∠C′GF=∠HGF=38°，
∵D′M//BC，∠D′GB=∠C′GF=38°，
∴∠MD′G=38°，
∵∠C′=∠ED′G=∠H=90°，
∴∠ED′M=90°-∠MD′G=90°-38°=52°，
∴∠AED′=∠ED′M=52°，
∴∠DED′=180°-∠AED′=180°-52°=138°．
故答案为：138°．
【点睛】
本题主要考查了平行线的性质及折叠的性质，熟练应用平行线的性质及折叠的性质进行求解是解决本题的关键．
23．（2021·浙江杭州·七年级期中）如图（1）是由两块形状相同的三角板拼成，已知，，点E是边上的动点，连结，将三角形沿直线翻折，点C，D的对应点分别为N，M，则：
（1）如图（2），当点N恰好落在边上时，的度数是___________；
（2）当与三角形的一边平行时，的度数为________．
【答案】 75° 105°或60°或45°
【解析】
【分析】
（1）利用折叠的性质判断出AD∥BC，利用平行线的性质可得结果；
（2）分MN∥AC，MN∥AB，MN∥BC，三种情况，分别求解．
【详解】
解：（1）当点N落在AB上时，由折叠可知：
∠DAC=∠MAN=60°，∠CAE=∠BAE=45°，
∵∠ACB+∠ACD=60°+30°=90°，∠D=90°，
∴AD∥BC，
∴∠AEC=180°-∠DAE=180°-45°-60°=75°；
（2）由（1）可得：AD∥BC，
如图3，MN∥AC，
∠AMN+∠BAC=90°+90°=180°，
可知点M在AB上，
∴∠CAN=90°-60°=30°，
由折叠可知：∠CAE=∠NAE=30°÷2=15°，
∴∠DAE=∠DAC+∠CAE=60°+15°=75°，
∴∠AEC=180°-75°=105°；
如图4，MN∥AB，
∴∠BAM=90°，∠BAN=∠N=30°，
∴∠NAC=30°+90°=120°，
由折叠可知：∠CAE=∠NAE=60°，
∴∠AEC=180°-∠CAE-∠CAD=60°；
如图5，MN∥BC，
∴∠M=∠MAD=90°，
∴∠NAC=360°-∠MAN-∠DAC-∠MAD=150°，
由折叠可知：∠NAE=∠CAE=75°，
∴∠AEC=180°-∠CAE-∠DAC=45°；
综上：∠AEC的度数为105°或60°或45°，
故答案为：（1）75°；（2）105°或60°或45°．
【点睛】
本题考查了折叠的性质，平行线的判定和性质，解题的关键是根据图形的变形分类讨论．
24．（浙江·三模）如图，在中，沿的平分线折叠，剪掉重复部分；将余下部分沿的平分线折叠，剪掉重复部分……将余下部分沿的平分线折叠，点与点重合，无论折叠多少次，只要最后一次恰好重合，则称是的好角．
（1）若经过次折叠是的好角，则与（设）之间的等量关系为________．
（2）若一个三角形的最小角是4°，且该三角形的三个角均是此三角形的好角．请写出符合要求三角形的另两个角的度数________．（写出一种即可）
【答案】 ∠B=n∠C 4、172或8、168或16、160或44、132或88°、88°
【解析】
【分析】
（1）根据折叠的性质、根据三角形的外角定理知∠A1A2B2=∠C+∠A2B2C=2∠C；
根据四边形的外角定理知∠BAC+2∠B-2C=180°①，根据三角形ABC的内角和定理知∠BAC+∠B+∠C=180°②，由①②可以求得∠B=3∠C；利用数学归纳法，根据展示的三种情形得出结论：∠B=n∠C；
（2）利用（1）的结论知∠B=n∠C，∠BAC是△ABC的好角，∠C=n∠A，∠ABC是△ABC的好角，∠A=n∠B，∠BCA是△ABC的好角；然后三角形内角和定理可以求得另外两个角的度数可以是4、172；8、168；16、160；44、132；88°、88°．
【详解】
解：（1）∠B=n∠C；
如图所示，在△ABC中，沿∠BAC的平分线AB1折叠，剪掉重复部分；
将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重复部分，
将余下部分沿∠B2A2C的平分线A2B3折叠，点B2与点C重合，
则∠BAC是△ABC的好角．
证明如下：∵根据折叠的性质知，∠B=∠AA1B1，∠C=∠A2B2C，∠A1B1C=∠A1A2B2，
∴根据三角形的外角定理知，∠A1A2B2=∠C+∠A2B2C=2∠C；
∵根据四边形的外角定理知，∠BAC+∠B+∠AA1B1-∠A1B1C=∠BAC+2∠B-2∠C=180°，
根据三角形ABC的内角和定理知，∠BAC+∠B+∠C=180°，
∴∠B=3∠C；
由展示的情形一知，当∠B=∠C时，∠BAC是△ABC的好角；
由展示的情形二知，当∠B=2∠C时，∠BAC是△ABC的好角；
由展示的情形三知，当∠B=3∠C时，∠BAC是△ABC的好角；
故若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为∠B=n∠C；
故答案为：∠B=n∠C．
（2）由（1）知设∠A=4°，∵∠C是好角，
∴∠B=4n°；
∵∠A是好角，
∴∠C=m∠B=4mn°，其中m、n为正整数得4+4n+4mn=180，
∴如果一个三角形的最小角是4°，
三角形另外两个角的度数是4、172；8、168；16、160；44、132；88°、88°．
故答案为：4、172；8、168；16、160；44、132；88°、88°．
【点睛】
本题考查了翻折变换（折叠问题）．解答此题时，充分利用了三角形内角和定理、三角形外角定理以及折叠的性质．难度较大．
25．（2022·吉林长春·七年级期末）【感知】如图①，在△ABC中，，．则______°．
【操作】如图②，点D、E分别在图①中的△ABC的边AC、AB上，且均不与△ABC的顶点重合，连接DE，将△ABC沿DE折叠，使点A的对称点始终落在四边形BCDE的外部，交边AB于点F，且点与点C在直线AB的异侧．则______°．
【探究】如图③，设图②中的，．
（1）求的度数．
（2）当的某条边与BC平行时，直接写出的度数．
【答案】【感知】50 【操作】220 【探究】（1）80° （2）的大小为45°或25°．
【解析】
【分析】
感知：根据三角形内角和定理可得的度数；
操作：根据四边形的内角和定理计算即可；
探究：（1）根据可得；再由折叠，得，可得，据此求解即可；
（2）分两种情况：或时，分别求解即可．
【详解】
感知：∵在△ABC中，，，
∴
操作：∵在四边形中，，，
∴
探究：（1）∵
∴①，
由折叠，得，
∴在中，②
∴①-②得：；
（2）如图，当时，
则，
∵
∴
由折叠性质得；
如图，当时，
则，
；
如图，当时，不符合题意，
综上所述，的大小为45°或25°．
【点睛】
本题考查的是三角形内角和定理，四边形的内角和定理，平行的性质和折叠的性质，熟悉相关性质并能熟练应用是解决本题的关键．
26．（2021·四川·成都教育科学研究院附属学校七年级期中）已知，直线PQMN，点C是直线PQ和MN之间的一点．
(1)如图1，点D，E分别在PQ，MN上，∠1和∠2为锐角，求证：∠C=∠1+∠2；
(2)把一块三角板ABC（其中∠A=30°，∠C=90）按如图2放置，点D，E分别是三角板的两直角边分别与平行线的交点，若∠AEN=∠A，求∠BDQ的度数；
(3)如图3，将（2）中的三角板进行适当的转动，把射线EM沿直线AC翻折，交BC于点F，试判断∠BDQ和∠FEN有何数量关系?写出你的结论并说明理由．
【答案】(1)见解析
(2)60°
(3)∠BDQ，理由见解析
【解析】
【分析】
1）过C作CH∥PQ，依据平行线的性质，即可得出∠C＝∠1＋∠2；
（2）根据（1）中的结论可得，∠C＝∠MEC＋∠PDC＝90°，再根据对顶角相等即可得出结论；
（3）根据邻补角的定义以及翻折的性质，可得，由（1）的结论可得∠C＝∠MEC＋∠PDC＝90°，再根据对顶角相等即可得出结论．
(1)
如图1，过C作CH∥PQ，
∵PQ∥MN，
∴CH∥MN，
∴∠1＝∠DCH，∠2＝∠ECH，
∴∠DCE＝∠DCH＋∠ECH＝∠1＋∠2．
(2)
∵∠AEN＝∠A＝30°，
∴∠MEC＝30°，
由（1）可得，∠C＝∠MEC＋∠PDC＝90°，
∴∠PDC＝90°−∠MEC＝60°，
∴∠BDQ＝∠PDC＝60°；
(3)
∠BDQ，理由如下
射线EM沿直线AC翻折，交BC于点F，
即
∠C＝∠MEC＋∠PDC＝90°，
∠BDQ＝∠PDC
∠BDQ
【点睛】
本题主要考查了平行线的性质，以及翻折的性质，对顶角相等，邻补角的定义等知识的综合应用，解决问题的关键是作辅助线构造内错角，依据两直线平行，内错角相等进行求解．
27．（2022·北京朝阳·七年级期末）阅读下面材料：活动1利用折纸作角平分线
①画图：在透明纸片上画出（如图1-①）；②折纸：让的两边QP与QR重合，得到折痕QH（如图1-②）；③获得结论：展开纸片，QH就是的平分线（如图1-③）．
活动2利用折纸求角
如图2，纸片上的长方形ABCD，直线EF与边AB，CD分别相交于点E，F．将对折，点A落在直线EF上的点处，折痕EN与AD的交点为N；将对折，点B落在直线EF上的点处，折痕EM与BC的交点为M．这时的度数可知，而且图中存在互余或者互补的角．
解答问题：（1）求的度数；
（2）①图2中，用数字所表示的角，哪些与互为余角？
②写出的一个补角．
解：（1）利用活动1可知，EN是的平分线，EM是的平分线，所以 ， ．由题意可知，是平角．所以（∠ ＋∠ ）＝ °．
（2）①图2中，用数字所表示的角，所有与互余的角是： ；
②的一个补角是 ．
【答案】（1），，，90；（2）①∠1、∠2；②∠CME或∠NEB．
【解析】
【分析】
【详解】
解：（1）∵折叠
∴EN是的平分线，EM是的平分线，
∴∠NEA=∠NEA′=，∠BEM=∠B′EM=，
∵是平角．
∴∠NEM=∠NEA′+∠B′EM==+，
故答案为：，，，90；
（2）①∵∠1=∠2，∠A′EN=∠3，∠NEM=90°，
∴∠A′EN+∠1=∠NEM=90°，
∴互为余角为∠1和∠2，
故答案为：∠1、∠2；
②∵∠A′EN=∠3，∠3+∠NEB=180°，
∴∠A′EN的补角为∠NEB．
∵∠B=90°，
∴∠2+∠EMB=90°，
∴∠3=∠EMB，
∵∠CME+∠EMB=180°，
∴∠3+∠CME=180°，
∴∠A′EN的补角为∠CME，
∴∠A′EN的补角为∠CME或∠NEB．
故答案为∠CME或∠NEB．
【点睛】
本题考查折叠性质，平角，角平分线，余角性质，补角性质，掌握折叠性质，平角，角平分线，余角性质，补角性质是解题关键．
28．（2022·广东广州·七年级期末）如图，长方形纸片ABCD，点E，F，C分别在边AD，AB，CD上．将∠AEF沿折痕EF翻折，点A落在点A'处；将∠DEG沿折痕EG翻折，点D落在点D'处．
（1）如图1，若∠AEF＝40°，∠DEG＝35°，求∠A'ED'的度数；
（2）如图1，若∠A'ED'＝α，求∠FEG的度数（用含α的式子表示）；
（3）如图2，若∠A'ED'＝α，求∠FEG的度数（用含α的式子表示）．
【答案】（1）；（2）；（3）
【解析】
【分析】
（1）由折叠的性质，得到，，然后由邻补角的定义，即可求出答案；
（2）由折叠的性质，先求出，然后求出∠FEG的度数即可；
（3）由折叠的性质，先求出，然后求出∠FEG的度数即可．
【详解】
解：（1）将∠AEF沿折痕EF翻折，点A落在点A'处；将∠DEG沿折痕EG翻折，点D落在点D'处，
∴，，
∴；
（2）根据题意，则
，，
∵，
∴，
∴，
∴；
（3）根据题意，
，，
∵，
∴，
∴，
∴；
【点睛】
本题考查了折叠的性质，邻补角的定义，解题的关键是熟练掌握折叠的性质，正确得到，．
29．（2021·江苏南京·七年级期末）ABCD是长方形纸片的四个顶点，点E、F、H分别边AD、BC、AD上的三点，连接EF、FH．
（1）将长方形纸片的ABCD按如图①所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B′、C′、D′，点B′在FC′上，则∠EFH的度数为 ；
（2）将长方形纸片的ABCD按如图②所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B′、C′、D'（B′、C′的位置如图所示），若∠B'FC′＝16°，求∠EFH的度数；
（3）将长方形纸片的ABCD按如图③所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B′、C′，D′（B′、C′的位置如图所示）．若∠EFH＝n°，则∠B′FC′的度数为 ．
【答案】（1）90°；（2）98°；（3）180°﹣2n°
【解析】
【分析】
（1）由折叠可得∠BFE＝∠B′FE，∠CFH＝∠C′FH，进而得出∠EFH＝（∠B′FB+∠C′FC），即可得出结果；
（2）可设∠BFE＝∠B′FE＝x，∠CFH＝∠C′FH＝y，根据2x+16°+2y＝180°，得出x+y＝82°，进而得到∠EFH；
（3）可设∠BFE＝∠B′FE＝x，∠CFH＝∠C′FH＝y，即可得到x+y＝180°﹣n°，再根据∠EFH＝∠B′FE+∠C′FH﹣∠B′FC′＝x+y﹣∠B′FC′，即可得到∠B′FC′．
【详解】
解：（1）∵沿EF、FH折叠，
∴∠BFE＝∠B′FE，∠CFH＝∠C′FH，
∵点B′在C′F上，
∴∠EFH＝∠B′FE+∠C′FH＝（∠B′FB+∠C′FC）＝×180°＝90°，
故答案为：90°；
（2）∵沿EF、FH折叠，
∴可设∠BFE＝∠B′FE＝x，∠CFH＝∠C′FH＝y，
∵∠B'FC′＝16°，
∴2x+16°+2y＝180°，
∴x+y＝82°，
∴∠EFH＝x+16°+y＝16°+82°＝98°；
（3）∵沿EF、FH折叠，
∴可设∠BFE＝∠B′FE＝x，∠CFH＝∠C′FH＝y，
∴∠EFH＝180°﹣（∠BFE+∠CFH）＝180°﹣（x+y），
∵∠EFH＝n°，
∴x+y＝180°﹣n°，
∵∠EFH＝∠B′FE+∠C′FH﹣∠B′FC′＝x+y﹣∠B′FC′，
∴∠B′FC′＝x+y﹣∠EFH＝180°﹣n°﹣n°＝180°﹣2n°，
故答案为：180°﹣2n°．
【点睛】
本题考查了折叠的性质，角度的和差，平角的定义，掌握角度的计算是解题的关键．
30．（2022·江苏宿迁·七年级期末）如图1，已知直线，点E、F分别在直线AB、CD上，G点为射线FD上一动点，且，将沿着EF翻折得到，直线EQ平分交直线CD于点P．
(1)当时，
①若，则______．
②若去掉条件“”，你还能求出的度数吗？试一试．
(2)如图2，在点G运动的过程中，当时，求的度数（用含a的代数式表示）
(3)在点G运动的过程中，若，且，直接写出的度数．
【答案】(1)①45°，②45°
(2)的度数为
(3) 或 .
【解析】
【分析】
（1）①由翻折可知: ，根据平行线的性质，可得,，角平分线的定义可得,根据，即可求解；②由翻折可知: ,进而可得，根据角平分线的定义可得，，根据，即可求解；
（2）在点运动过程中，当时，，由翻折可知：，根据角平分线的定义可得，计算即可求解．
（3）由（2）可知：在点运动过程中，，在点 运动的过程中, 若 , 且 , 则，分点 在点 的右侧时与点 在点 的左侧时两种情形列出方程，解方程即可求解．
(1)
解：①若 , 则 ,
由翻折可知: ,
,
,
,
,
平分 ,
,
,
,
故答案为: ;
②若去掉条件, 还能求出 的度数,
,
,
由翻折可知: ,
,
,
平分 ,
(2)
解：在点运动过程中，当时，，
由翻折可知：
,
,
平分 ,
,
；
即的度数为；
(3)
解：由（2）可知：在点运动过程中，，
在点 运动的过程中, 若 , 且 , 则
，
点 在点 的右侧时
，

解得: ;
点 在点 的左侧时，
，

解得: ，
综上所述, 的度数为 或 ．
【点睛】
本题考查了平行线的性质求角度，折叠的性质，角平分线的性质，三角形内角和定理的应用，数形结合是解题的关键．
31．（2021·浙江·七年级期中）如图1，三角形中，，，．点D是边上的定点，点E在边上运动，沿折叠三角形，点C落在点G处．
（1）如图2，若，求的度数．
（2）如图3，若，求的度数．
（3）当三角形的三边与三角形的三边有一组边平行时，直接写出其他所有情况下的度数．
【答案】（1）52°；（2）142°；（3）116°或26°或38°或64°
【解析】
【分析】
（1）根据折叠的性质得到∠CDE=∠A=∠GDE=64°，即可求出∠ADG；
（2）根据GE∥AB，得到∠BEG=90°，算出∠BFD，利用四边形内角和即可求出∠ADG；
（3）找出其他所有情况，画出图形，利用平行线的性质求解即可．
【详解】
解：（1）由折叠可知：
∠C=∠DGE=26°，∠CDE=∠GDE，
∵DE∥AB，AB⊥BC，
∴DE⊥BC，则G在BC上，
∴∠CDE=∠A=∠GDE=64°，
∴∠ADG=180°-64°×2=52°；
（2）由折叠可知：∠C=∠DGE=26°，∠CDE=∠GDE，∠DEC=∠DEG，
∵GE∥AB，
∴∠B=∠CEG=∠BEG=90°，
∴∠EFG=90°-26°=64°，
∵∠A=64°，∠B=90°，
∴∠ADG=360°-64°-90°-64°=142°；
（3）如图，DG∥AB，
则∠ADG=180°-∠A=116°；
如图，DG∥BC，
∠ADG=∠C=26°；
如图，EG∥AC，
∠ADG=∠G=∠C=26°；
如图，EG∥AB，
∴∠A=∠CFE=64°，∠B=∠CEG=90°，
由折叠可知：∠DEG=∠DEC=45°，
∴∠CDE=180°-45°-26°=109°=∠EDG，
∴∠EDF=180°-109°=71°，
∴∠ADG=109°-71°=38°；
如图，DG∥AB，
∴∠ADG=∠A=64°；
综上：其他所有情况下∠ADG的度数为116°或26°或38°或64°．
【点睛】
本题考查了平行线的性质，折叠问题，解题的难点在于找出所有符合题意的情况，得到角的关系．
32．（陕西·西安市铁一中学七年级阶段练习）如果两个角之差的绝对值等于，则称这两个角互为“互优角”，即若，则称和互为“互优角”（本题中所有角都是大于且小于的角）
图1 图2 图3
（1）若和互为“互优角”，当时，则________；
（2）如图1，将一长方形纸片沿着对折，（点在线段上，点在线段上），使点落在，若与互为“互优角”，则的度数为________；
（3）再将纸片沿着对折（点在线段或上），使点落在．
①如图2，若点，，在同一直线上，且与互为“互优角”，求的度数（对折时，线段落在内部）；
②若与互为“互优角”，则与应满足什么样的数量关系（直接写出结果即可）．
【答案】（1）30°或150°；（2）40°或80°；（3）①∠EPF=80°；②∠BPE+∠CPF的度数为60°或100°或140°．
【解析】
【分析】
（1）按照“互优角”的定义写出式子，解方程即求出∠2；
（2）由∠EPB'+∠EPB'+∠EPB′+60°=180°即可求；
（3）①由∠BPE+∠EPB′+∠B′PF+∠FPC=180°，即可求；
②分三种情况讨论，根据折叠的性质以及平角的性质即可求．
【详解】
解：（1）∵∠1和∠2互为“互优角”，∠1=90°，
∴|∠1-∠2|=60°，
∴90°-∠2=60°或90°-∠2=-60°，
解得：∠2=30°或150°，
故答案为：30°或150°；
（2）∵∠EPB′与∠B′PC互为“互优角”，
当∠EPB′＜∠B′PC时，∠B′PC-∠EPB′=60°，
∴∠B′PC=∠EPB′+60°，
∵△BEP翻折得△B'EP，
∴∠EPB=∠EPB'，
∵∠EPB+∠EPB'+∠B′PC=180°，
∴∠EPB'+∠EPB'+∠EPB′+60°=180°，
解得：∠EPB′=40°；
当∠EPB′＞∠B′PC时，∠EPB′-∠B′PC=60°，
同理可得∠EPB′=80°．
综上所述，∠EPB的值为40°或80°；
故答案为：40°或80°；
（3）①∵点E、C′、P在同一直线上，且∠B′PC′与∠EPF互为“互优角”，
∵对折时，线段落在内部
∴∠B′PC′＜∠EPF，∠EPF-∠B′PC′=60°=∠B′PF，
∵∠BPE=∠B′PE=∠EPF-60°，∠FPC=∠EPF，
∴∠BPE+∠EPB′+∠B′PF+∠FPC=180°，
∴∠EPF-60°+∠EPF+∠EPF=180°，
解得∠EPF=80°；
②当点F在边CD上时，如图：
显然∠EPF>∠B′PC′，
∵∠B′PC′与∠EPF互为“互优角”，
∴∠EPF-∠B′P′C=60°，
根据折叠的性质：∠B′PE=∠1，∠FPC′=∠2，
∴∠EPF=∠1+∠2+∠B′P′C，
∴∠EPF-∠B′P′C=∠1+∠2+∠B′P′C-∠B′P′C=∠1+∠2=60°，
即∠BPE+∠CPF=60°；
当点F在边AD上，且当∠EPF>∠B′PC′时，如图：
∠B′PC′与∠EPF互为“互优角”，
∴∠EPF-∠B′P′C =60°，
根据折叠的性质：∠B′PE=∠1，∠FPC′=∠2，
∴∠EPF=∠1+∠2-∠B′P′C，
∴∠EPF-∠B′P′C =∠1+∠2-2∠B′P′C =60°，
∠1+∠EPF+∠2=∠1+∠1+∠2-∠B′P′C+∠2=2(∠1+∠2) -∠B′P′C=180°，
解得：∠1+∠2=100°，
即∠BPE+∠CPF=100°；
当点F在边AD上，且当∠EPF