初中数学浙教版（2024）八年级下册2.1 一元二次方程说课ppt课件

这是一份初中数学浙教版（2024）八年级下册2.1 一元二次方程说课ppt课件，共5页。PPT课件主要包含了学习目标，交流合作，x2+3x4，3观察下面等式，知识讲解，x2-8x-200，观察下列三个方程，它们有什么共同特点，都是整式方程，一元二次方程等内容，欢迎下载使用。
1.理解一元二次方程及其相关概念，能够熟练地把一元二次方程化为一般形式．
2. 应用一元二次方程的解的定义解决有关问题．
3. 在分析、揭示实际问题中的数量关系，并把实际问题转化为数学模型的过程中，感受方程是刻画现实世界中的数量关系的工具，增强对一元二次方程的感性认识．
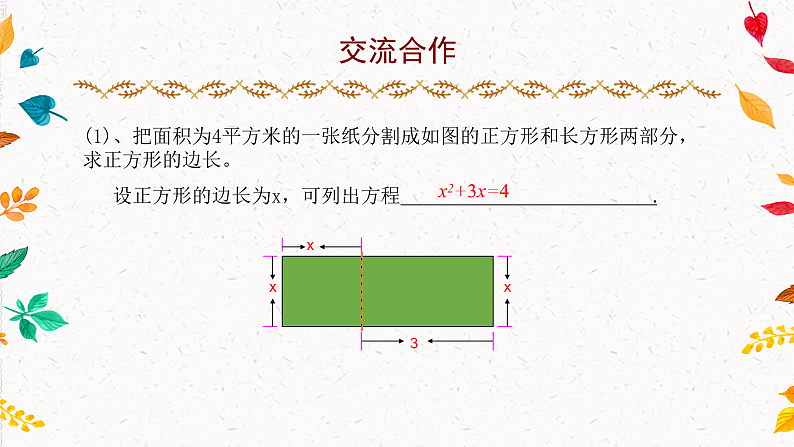
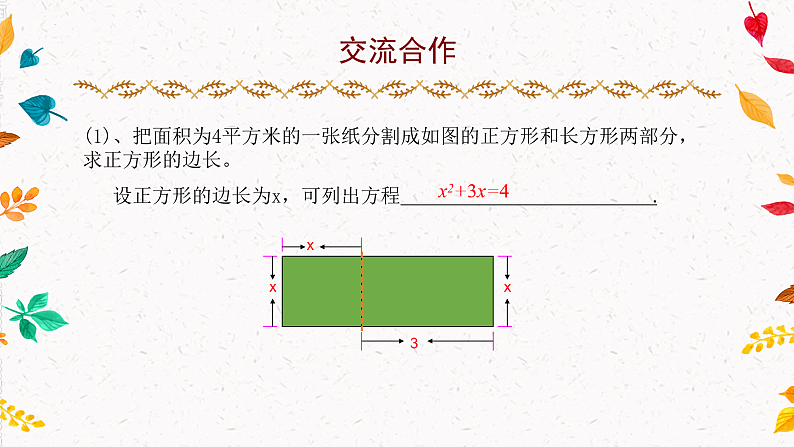
(1)、把面积为4平方米的一张纸分割成如图的正方形和长方形两部分，求正方形的边长。 设正方形的边长为x，可列出方程 .
你还能找到其他的五个连续整数，使前三个数的平方和等于后两个数的平方和吗？
设五个连续整数中第一个为x ，那么后四个数为 、 、 、 ，根据题意，得方程： .
1、只含有一个未知数；
4、都可以化成 的形式；
a 为二次项系数、b为一次项系数、c为常数，a≠0
3、未知数的最高次数为2；
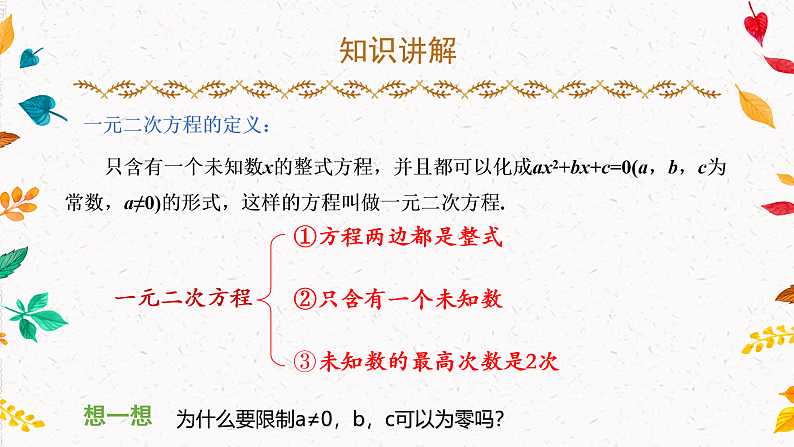
只含有一个未知数x的整式方程，并且都可以化成ax2+bx+c=0(a，b，c为常数，a≠0)的形式，这样的方程叫做一元二次方程.
一元二次方程的定义：
③未知数的最高次数是2次
为什么要限制a≠0，b，c可以为零吗？
一般地,任何一个关于x 的一元二次方程都可以化为 c为常数，a≠0) 的形式，我们把ax2+bx+c=0(a，b，c为常数，a≠0）称为一元二次方程的一般形式，其中ax2，bx，c分别称为二次项、一次项和常数项.
ax2+bx+c=0(a ，b ，
行业PPT模板http/hangye/
例1、把方程 化成一元二次方程的一般形式，并写出它的二次项系数、一次项系数和常数项.
化一般式的方法： 一去（去分母、去括号） 二移（移项） 三并（合并同类项）
例2 下列方程中哪些是一元二次方程？
(7)x(x-2)=x2+19
能使一元二次方程两边相等的未知数的值叫一元二次方程的解（或根）.
下列哪些数是方程 x2–x–6= 0 的根? -2, -1, 0, 1, 2, 3
例3 已知一元二次方程 2x2+bx+c=0 的两个根为 和 ，求这个方程。
∴这个方程是 2x2 + x -15 =0
例4 已知关于x的一元二次方程x2+ax+a=0的一个根是3，求a的值。
判断下列方程是否为一元二次方程：
① 10x2=9 ( ) ②2(x-1)=3x ( ) ③2x2-3x-1=0 ( ) ④ ( ) ⑤2xy-7=0 ( ) ⑥9x2=5-4x ( ) ⑦4x2=5x ( ) ⑧3y2+4=5y ( )
若关于x的一元二次方程（m+2)x2+5x+m2-4=0有一个根为0.求m的值.
解：将x=0代入方程m2-4=0， 解得m= ±2. ∵ m+2 ≠0， ∴ m ≠-2， 综上所述：m =2.
已知a是方程x2+2x－1=0 的一个实数根,求 2a2+4a+2018的值.
方法点拨：求代数式的值，先把已知解代入，再注意观察，有时需运用到整体思想，求解时，将所求代数式的一部分看作一个整体，再用整体思想代入求值．
若x＝3是关于x的方程2x2＋ax－6＝0的一个根，则a的值是 ． 根据题意，列出方程(不必解答)：(1)两个连续整数的积是210，求这两个数；(2)在一块长250 m、宽150 m的草地四周修一条路，路修好后草地的面积减少1 191 m2，求这条路的宽度．
设其中一个整数为x，则另一个整数为(x＋1)，依题意，得x(x＋1)＝210.
设这条路的宽为x m，则(250－2x)(150－2x)＝250×150－1191.