第1周 八年级上册数学北师大版（1.1-1.2）每周测验(含答案)

这是一份第1周 八年级上册数学北师大版（1.1-1.2）每周测验(含答案)，共10页。试卷主要包含了1-1，国是较早了解勾股定理的国家之一，观察下列勾股数等内容，欢迎下载使用。
1.如图是一棵美丽的勾股树,它是由正方形和直角三角形拼成的,若正方形A,B的面积分别为41,25,则正方形C的面积是( )
A.4B.5C.16D.66
2.我国是最早了解勾股定理的国家之一,它被记载于我国古代著名的数学著作《周髀算经》中.下列各组数中,是“勾股数”的是( )
A.2,3,4B.4,5,6C.7,8,9D.3,4,5
3.《勾股举隅》为梅文鼎研究中国传统勾股算术的著作,其中的主要成就是证明了勾股定理和对勾股算术算法进行了推广.书中的证明方法是将4个三边长分别为,,的全等直角三角形拼成如图1所示的五边形,然后通过添加辅助线,用面积法证明勾股定理.下面是小华给出的相关证明：
则下列说法错误的是( )
A.①代表B.②代表
C.③代表正方形D.④代表
4.如图所示的一块地,已知,,,,,则这块地的面积为( ).
A.B.C.D.
5.如图,网格中每个小正方形的边长都为1,是( ).
A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形
6.如图,在网格图(每个小方格均是边长为1的正方形)中,以AB为一边作直角三角形ABC,要求顶点C在格点上,则图中不符合条件的点是( )
A.B.C.D.
7.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为6和8,则b的面积为( )
A.6B.8C.10D.14
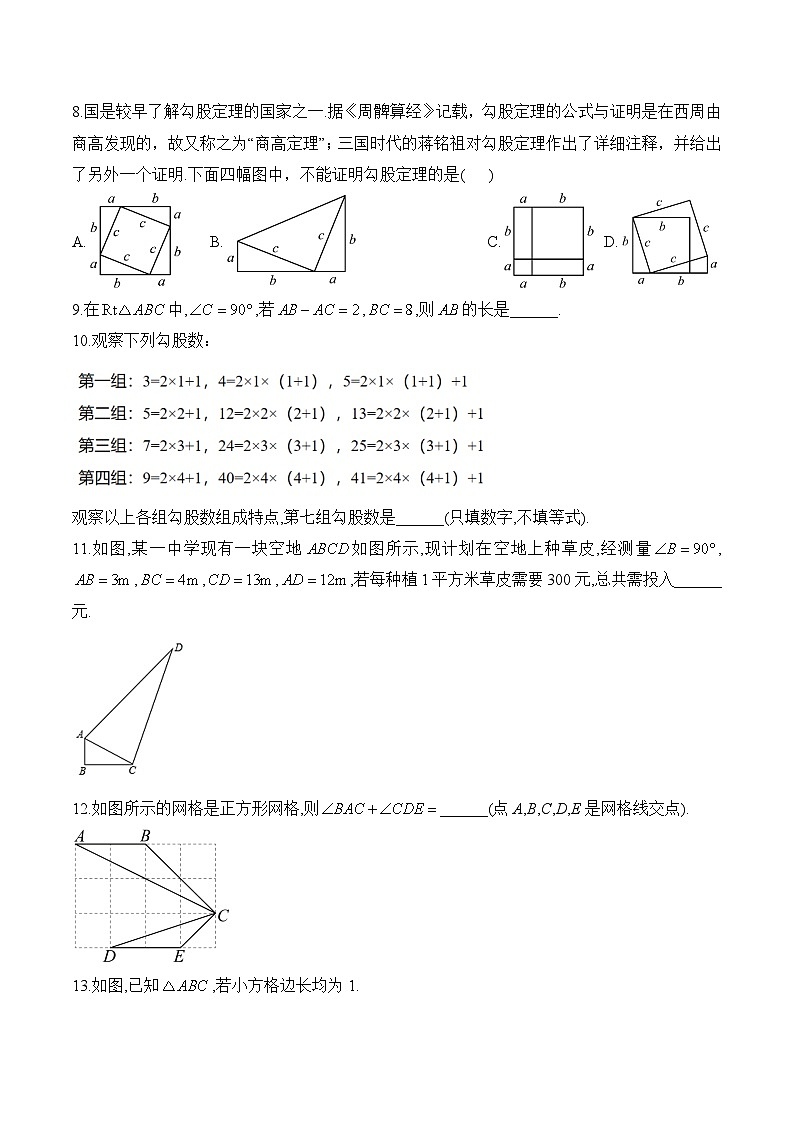
8.国是较早了解勾股定理的国家之一.据《周髀算经》记载，勾股定理的公式与证明是在西周由商高发现的，故又称之为“商高定理”；三国时代的蒋铭祖对勾股定理作出了详细注释，并给出了另外一个证明.下面四幅图中，不能证明勾股定理的是( )
A.B.C.D.
9.在中,,若,,则的长是______.
10.观察下列勾股数：
观察以上各组勾股数组成特点,第七组勾股数是______(只填数字,不填等式).
11.如图,某一中学现有一块空地如图所示,现计划在空地上种草皮,经测量,,,,,若每种植1平方米草皮需要300元,总共需投入______元.
12.如图所示的网格是正方形网格,则______(点A,B,C,D,E是网格线交点).
13.如图,已知,若小方格边长均为1.
(1)求的面积；
(2)判断的形状,并说明理由.
14.清代扬州数学家罗士琳痴迷研究勾股定理，提出推算勾股数的“罗士琳法则”，其中有一个法则是“如果k是大于2的偶数，那么k，k的一半的平方减1，k的一半的平方加1是一组勾股数”.
(1)当时，写出这一组勾股数______.
(2)证明“罗士琳法则”的正确性.
答案以及解析
1.答案：C
解析：根据勾股定理,可知,以直角边为边长的正方形的面积和等于以斜边为边的正方形的面积,
即：,
,
故选：C.
2.答案：D
解析：A、,这组数不是勾股数,不符合题意；
B、,这组数不是勾股数,不符合题意；
C、,这组数不是勾股数,不符合题意；
D、,这组数是勾股数,符合题意；
故选：D.
3.答案：C
解析：如图所示,延长交于G,
方法一：将五边形看成是由正方形与,拼成,则；
方法二：将五边形看成是由正方形,正方形,,拼成,则,
根据面积相等可以得到,即,
故选：C.
4.答案：C
解析：如图所示,连接AC.在中,,,,.又,
是直角三角形.
这块地的面积的面积的面积.
故选:C.
5.答案：A
解析：∵,,,,
,
即,,,
∴不是直角三角形,不是等腰三角形.
∵是钝角三角形,
∴是锐角三角形.
故选：A.
6.答案：D
解析：,,,
,
是直角三角形,
,,,
是直角三角形,
,,,
,
是直角三角形,
,,,
不是直角三角形,
所以,,是直角三角形,但不是直角三角形,
故选:D.
7.答案：D
解析：如图,
∵a、b、c都为正方形,
∴,,,,
∵,,
∴,
在和中,
,
∴,
∴,
在中,,
∴b的面积为14.
故选：D.
8.答案：C
解析：A.大正方形的面积为：，也可看作是4个直角三角形和一个小正方形组成，则其面积为：，，故本选项不符合题意；
B.梯形的面积为：，也可看作是2个直角三角形和一个等腰直角三角形组成，则其面积为：，，可以证明勾股定理，故本选项不符合题意；
C.图形中不涉及直角三角形，故无法证明勾股定理，故本选项符合题意；
D.图中图形面积等于边长为c的正方形面积，加上两个直角边分别为a、b的长方形面积，即其面积为：，也可看作是一个梯形面积加上一个等腰直角三角形的面积，则其面积为：，，故本选项不符合题意；
故选：C.
9.答案：17
解析：∵在中,,,,
∴,
即,
解得.
故答案为：17.
10.答案：15,112,113
解析：观察可以发现：第n组勾股数为,,,
当时,勾股数为：,,.
故答案为：15,112,113.
11.答案：10800
解析：在中
,
.
在中,,而,即
,.
所以需费用:(元).
故答案为:10800.
12.答案：
解析：连接AD,如图：
∵,,,
即,
∴是等腰直角三角形,且,
∴,
∵,,
∴,
故答案为：.
13.答案：(1)
(2)为直角三角形,理由见解析
解析：(1),
∴的面积为5；
(2)为直角三角形,
理由：∵小方格边长为1,
∴,
,
,
∴,
∴为直角三角形.
14.答案：(1)14，48，50
(2)见解析
解析：(1)当时，
根据题意得：，
∴这一组勾股数为14，48，50；
故答案为：14，48，50.
(2)证明：∵
.
，
∴当k大于2时，，
∴如果k是大于2的偶数，那么k，k的一半的平方减1，k的一半的平方加1是一组勾股数.
如图2,延长交_____①_____于点G.
用两种不同的方法表示五边形的面积S：
方法一：将五边形看成是由正方形与,拼成,则_____②_____.
方法二：将五边形看成是由_____③_____,正方形,,拼成,则.
根据面积相等可以得到_____④_____,即.