华东师大版（2024）九年级下册1. 二次函数y=ax2的图象与性质备课课件ppt

这是一份华东师大版（2024）九年级下册1. 二次函数y=ax2的图象与性质备课课件ppt，共12页。PPT课件主要包含了学习目标，重难点，情景导入，教学过程，探究新知，知识归纳，例题精讲等内容，欢迎下载使用。
1.会用描点法画出二次函数y=ax2(a≠0)的图象,掌握二次函数y=ax2(a≠0)的性质.2.经历探索二次函数 y =ax2(a≠0)的图象与性质的过程,能运用二次函数y=ax2(a≠0)的图象及性质解决简单的实际问题,掌握数形结合的数学思想方法.
重点：会画二次函数y=ax2(a≠0)的图象,理解有关概念及图象性质. 难点：对二次函数研究的途径和方法的体悟.
1.用描点法画函数图象有哪些步骤? 答:列表、描点、连线.2.一次函数、反比例函数的图象是什么? 答:一次函数的图象是一条直线,反比例函数的图象是双曲线.3.对于函数y=x2 ,取一些x,y的对应值在坐标系内描点,这些点会在同一直线上吗? 答:不会.
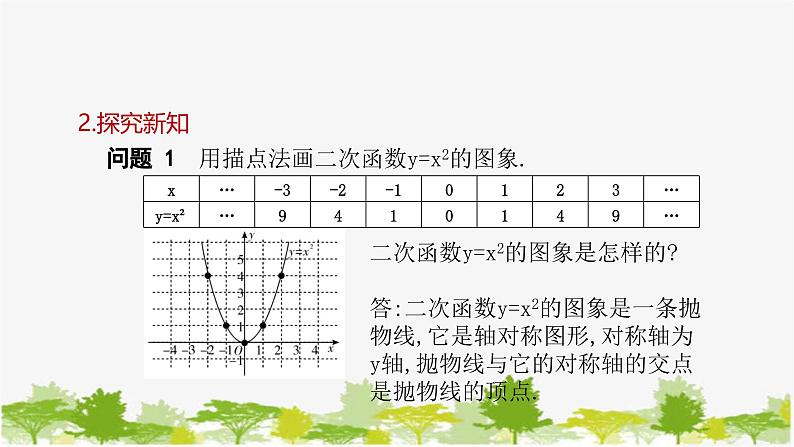
问题 1 用描点法画二次函数y=x2的图象.
二次函数y=x2的图象是怎样的?答:二次函数y=x2的图象是一条抛物线,它是轴对称图形,对称轴为y轴,抛物线与它的对称轴的交点是抛物线的顶点.
我们把形如y=ax2(a≠0)这样的图象通常叫做抛物线,它是轴对称图形,对称轴为y轴,抛物线与它的对称轴的交点是抛物线的顶点.
问题 2 (1)你能描述y=x2与y=-x2的形状吗? (2)y=x2与y=-x2 图象是轴对称图形吗?如果是,它们的对称轴是什么? (3)y=x2与y=-x2图象与x轴有交点吗?如果有,交点坐标是什么? (4)在y=x2与y=-x2中,在对称轴左侧,随着x值的增大,y的值如何变化?在对称轴右侧呢? (5)在y=x2中,当x取什么值时,y的值最小?最小值是什么?在y=-x2中呢?
答:(1)二次函数y=x2与y=-x2的图象形状都是抛物线. (2)是,抛物线关于y轴对称,即对称轴为y轴. (3)有,(0,0). (4)在y=x2中,在对称轴的左侧,y随着x的增大而减小;在对称轴的右侧,y 随着x的增大而增大.在y=-x2中,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x的增大而减小. (5)在y=x2中,当x=0时,y值最小为0,在y=-x2中,当x=0时,y值最大为0.
1.二次函数y=ax2(a≠0)的图象是一条抛物线;2.当a>0时,抛物线的开口向上,图象有最低点;当a0时,在对称轴左侧,图象呈下降趋势,y随x的增大而减小,在对称轴右侧,图象呈上升趋势,y随x的增大而增大.
例1 函数y=-6x2的图象开口向下,顶点坐标是 (0,0) ,对称轴是 y轴 ,当x= 0 时,函数y=-6x2有最大 大 (选填“大”或“小”)值,这个值为 0 .例2 已知抛物线y=ax2(a≠0)经过点A(-2,-8). (1)求此抛物线的函数表达式; (2)判断点 B(-1,-4)是否在此抛物线上. 解:(1)把(-2，-8)代入y=ax2,得-8=a(-2)2,解出a=-2, ∴此抛物线的函数表达式为y=-2x2. (2)当x=-1时,-2×(-1)2=-2≠-4, ∴点B(-1,-4)不在此抛物线上.
4.巩固练习 完成教材课后同步练习