初中数学华师大版九年级下册1. 二次函数y=ax2的图象与性质教案及反思

26．2　二次函数的图象与性质

1　二次函数y＝ax2的图象与性质(第1课时)

教学目标

一、基本目标

1．能够用描点法作出二次函数y＝ax2的图象．

2．经历探索二次函数y＝ax2的图象与性质的过程，体会数形结合的思想方法．

二、重难点目标

【教学重点】

二次函数y＝ax2的图象的画法，理解函数y＝ax2的图象．

【教学难点】

二次函数y＝ax2的图象与性质．

教学过程

环节1　自学提纲，生成问题

【5 min阅读】

阅读教材P5～P7的内容，完成下面练习．

【3 min反馈】

1．用描点法画函数图象的一般步骤：列表、描点、连线.

2．抛物线y＝x2中的开口方向是向上，顶点坐标是(0,0)，对称轴是y轴.抛物线y＝－x2的开口方向是向下，顶点坐标是(0,0)，对称轴是y轴.

3．一般地，当a>0时，抛物线y＝ax2的开口向上，对称轴是y轴，顶点是原点，顶点是抛物线的最低点，a越大，抛物线的开口越小.当a<0时，抛物线y＝ax2的开口向下，对称轴是y轴，顶点是原点，顶点是抛物线的最高点，a越小，抛物线的开口越小.

4．对于二次函数y＝ax2的图象：如果a>0，当x<0时，y随x的增大而减小，当x>0时，y随x的增大而增大；如果a<0，当x<0时，y随x的增大而增大，当x>0时，y随x的增大而减小.

环节2　合作探究，解决问题

活动1　小组讨论(师生互学)

【例1】在同一直角坐标系中画出函数y＝x2与y＝2x2的图象．

【互动探索】(引发学生思考)用描点法可以画出函数的图象．

【解答】列表如下：

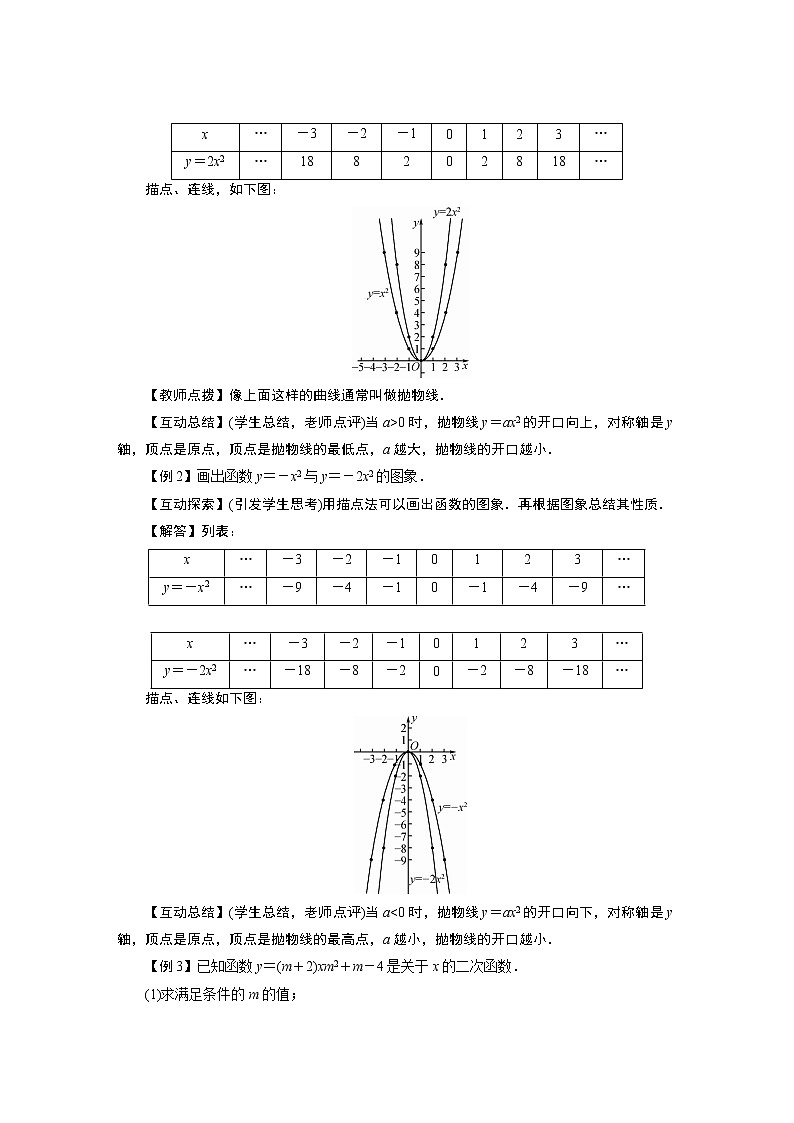
描点、连线，如下图：

【教师点拨】像上面这样的曲线通常叫做抛物线．

【互动总结】(学生总结，老师点评)当a>0时，抛物线y＝ax2的开口向上，对称轴是y轴，顶点是原点，顶点是抛物线的最低点，a越大，抛物线的开口越小．

【例2】画出函数y＝－x2与y＝－2x2的图象．

【互动探索】(引发学生思考)用描点法可以画出函数的图象．再根据图象总结其性质．

【解答】列表：

描点、连线如下图：

【互动总结】(学生总结，老师点评)当a<0时，抛物线y＝ax2的开口向下，对称轴是y轴，顶点是原点，顶点是抛物线的最高点，a越小，抛物线的开口越小．

【例3】已知函数y＝(m＋2)xm2＋m－4是关于x的二次函数．

(1)求满足条件的m的值；

(2)m为何值时，抛物线有最低点？求这个最低点；当x为何值时，y随x的增大而增大？

【互动探索】(引发学生思考)一个函数是二次函数必须满足什么条件？二次函数y＝ax2的性质有哪些？这些性质与a有什么关系？

【解答】(1)由题意，得

解得

∴当m＝2或m＝－3时，原函数为二次函数．

(2)若抛物线有最低点，则抛物线开口向上，

∴m＋2>0，即m>－2，

∴只能取m＝2.

∵这个最低点为抛物线的顶点，其坐标为(0,0)，

∴当x>0时，y随x的增大而增大．

【互动总结】(学生总结，老师点评)(1)y＝axm为二次函数的前提条件是a≠0，且自变量x的最高次数为2.(2)二次函数y＝ax2的性质：当a＞0时，开口向上．x＞0时，y随x的增大而增大．x＜0时，y随x的增大而减小．函数的最小值为0.顶点坐标为(0,0)；当a＜0时，开口向下．当x＞0时，y随x的增大而减小．x＜0时，y随x的增大而增大．函数的最大值为0.顶点坐标为(0,0)．

活动2　巩固练习(学生独学)

1．二次函数y＝ax2与一次函数y＝－ax(a≠0)在同一坐标系中的图象大致是(　B　)

2．函数y＝(－x)2的图象是抛物线，顶点坐标是(0,0)，对称轴是y轴，开口方向是向上.当x<0时，y的值随x值的增大而减小.

3．函数y＝x2，y＝x2，y＝－2x2图象如图所示，请指出三条抛物线的名称．

解：如图所示．

活动3　拓展延伸(学生对学)

【例4】已知抛物线y＝ax2(a≠0)与直线y＝x－3交于点(1，b)．

(1)求a，b的值；

(2)x取何值时，二次函数中的y随x的增大而增大？

【互动探索】将点(1，b)代入y＝x－3得b的值，再将其代入y＝ax2得a的值．

【解答】(1)把(1，b)代入y＝x－3，得b＝1－3＝－2，

∴点的坐标为(1，－2)．

把(1，－2)代入y＝ax2，得－2＝a，即a＝－2.

∴a＝－2，b＝－2.

(2)由(1)可得y＝－2x2，

∴抛物线开口向下，且对称轴为y轴，

∴当x＜0时，y随x的增大而增大．

【互动总结】(学生总结，老师点评)抛物线与直线的交点即为同时满足抛物线方程、直线方程的点，将这个点的坐标代入抛物线解析式、直线解析式均成立．

环节3　课堂小结，当堂达标

(学生总结，老师点评)

练习设计

请完成本课时对应训练！