高中数学沪教版（2020）必修第二册8.4 向量的应用优质课件ppt

这是一份高中数学沪教版（2020）必修第二册8.4 向量的应用优质课件ppt，共27页。PPT课件主要包含了勾股定理及其逆定理，求面积，证垂直，证共线等内容，欢迎下载使用。
例：已知　　 的坐标分别为　　　　　　　　 ,求点P的坐标 。
P是△ABC所在平面内任一点.G是△ABC的重心
平行四边形是矩形当且仅当对角线相等
平行四边形是菱形当且仅当对角线互相垂直的
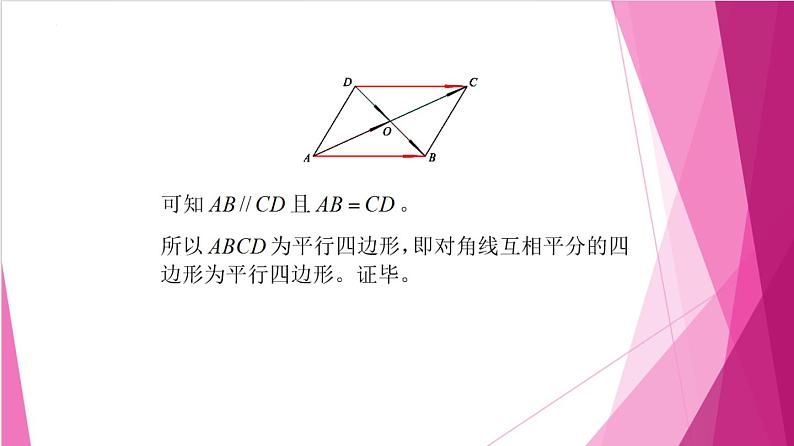
证明：对角线互相平分的四边形为平行四边形。
利用向量证明余弦定理。
利用平面向量证明三角公式两角差的余弦公式的证明
①简单描述下向量与几何和代数三者的关系。
②应用向量解决几何、代数和力学问题的基本方法有哪些？
③应用向量解决几何、代数和力学问题应注意的关键点有哪些？
“如今反思回顾，可见向量代数其实乃是坐标几何的返璞归真、精益求精，它使得几何和代数结合得更加真切自然、直截了当...这种返璞归真的向量运算，可以把解析几何的精要体现得更加简明朴实.”