

江苏无锡市东林中学2024-2025学年八上数学第10周阶段性训练模拟练习【含答案】
展开
这是一份江苏无锡市东林中学2024-2025学年八上数学第10周阶段性训练模拟练习【含答案】,共20页。试卷主要包含了给出下列4个命题等内容,欢迎下载使用。
1.以下各组数为边长的三角形,其中构成直角三角形的一组是( )
A.4、5、6B.3、5、6C.D.2,
2.给出下列4个命题:
①两边及其中一边上的中线对应相等的两个三角形全等;
②两边及其中一边上的高对应相等的两个三角形全等;
③两边及一角对应相等的两个三角形全等;
④有两角及其中一角的角平分线对应相等的两个三角形全等.
其中正确的个数有( )
A.1个B.2个C.3个D.4个
3.如图,在四边形ABCD中,对角线AC⊥BD,垂足为点O,且∠OAB=45°,OC=2OA=8,∠OCB=∠ODA,则四边形ABCD的面积为( )
A.32B.36C.42D.48
4.如图,在△ABC中,AB=AC,D为边BA的延长线上一点,且CD=AB,若∠B=32°,则∠D等( )
A.48°B.58°C.64°D.74°
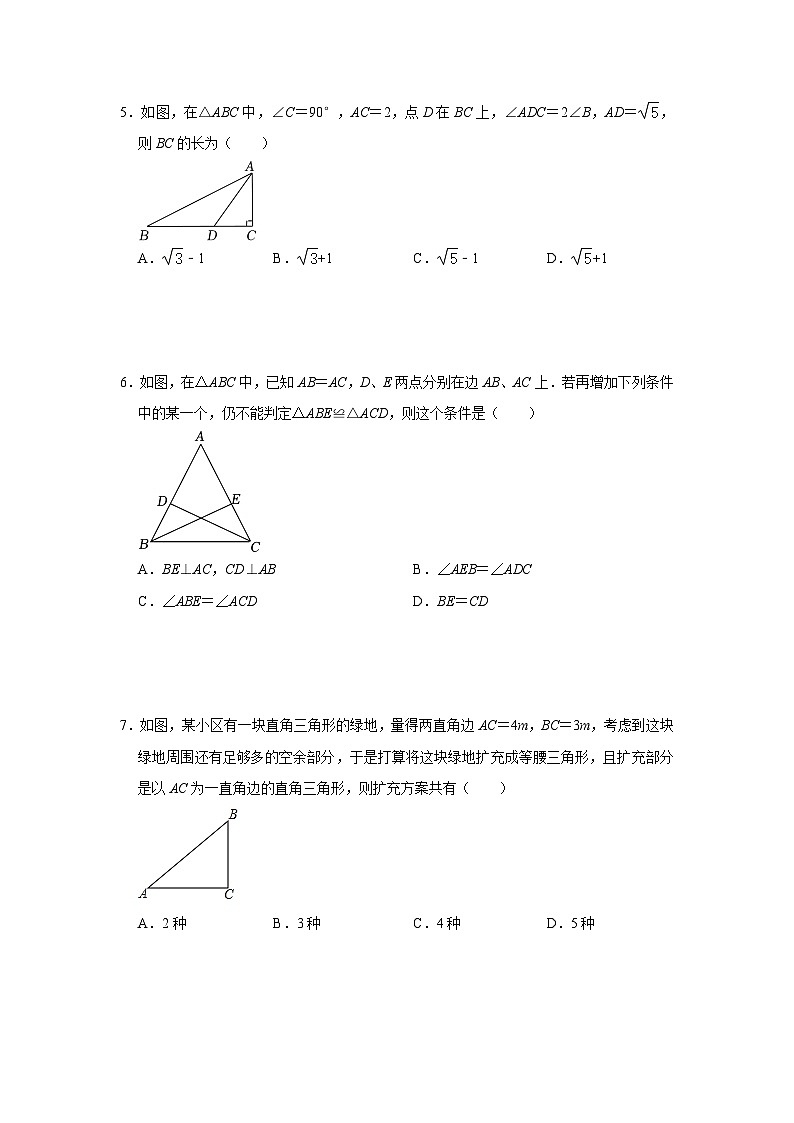
5.如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为( )
A.﹣1B.+1C.﹣1D.+1
6.如图,在△ABC中,已知AB=AC,D、E两点分别在边AB、AC上.若再增加下列条件中的某一个,仍不能判定△ABE≌△ACD,则这个条件是( )
A.BE⊥AC,CD⊥ABB.∠AEB=∠ADC
C.∠ABE=∠ACDD.BE=CD
7.如图,某小区有一块直角三角形的绿地,量得两直角边AC=4m,BC=3m,考虑到这块绿地周围还有足够多的空余部分,于是打算将这块绿地扩充成等腰三角形,且扩充部分是以AC为一直角边的直角三角形,则扩充方案共有( )
A.2种B.3种C.4种D.5种
二.填空题(共12小题)
8.如果等腰三角形的一个外角为80°,那么它的底角为 度.
9.若某个正数的两个平方根是a﹣3与a+5,则a= .
10.如图,△ABC中,D是BC上一点,AC=AD=DB,∠BAC=105°,则∠ADC= °.
11.已知一个直角三角形的一条直角边长为6,斜边上的中线长为5,则这个直角三角形的另一条直角边长为 .
12.若等腰三角形的周长为12,其中一边长为2,则另两边的长分别为 .
13.在△ABC中,已知∠C=90°,AC=4,BC=6,M、N分别为边AC、AB上的点,将△ABC沿MN折叠,若点A恰好落在BC的中点处,则CM的长为 .
14.如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为 cm.
15.如图,△ABC中,D是BC上一点,AC=AD=DB,∠BAC=120°,则∠ADC= .
16.如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为 .
17.若与(y+4)2互为相反数,则x+y的平方根为 .
18.分别以△ABC的各边为一边向三角形外部作正方形,若这三个正方形的面积分别为6cm2、8cm2、10cm2,则△ABC 直角三角形.(填“是”或“不是”)
19.如图,已知△ABC中,∠C=90°,BC=4,AC=5,将此三角形沿DE翻折,使得点A与B重合,则AE长为 .
三.解答题(共7小题)
20.某农户以1500元/亩的单价承包了15亩地种植板栗,每亩种植80株优质板栗嫁接苗,购买嫁接苗,购买价格为5元/株,且每亩地的管理费用为800元,一年下来喜获丰收平均每亩板栗产量为600kg,已知当地板栗的批发和;零售价格分别如下表所示:
通过市场调研发现,批发与零售的总销量只能达到总产量的70%,其中零售量不高于总销售量的40%,经多方协调当地食品加工厂承诺以7元/kg的价格收购该农户余下的板栗,设板栗全部售出后的总利润为y元,其中零售xkg.
(1)求y与x之间的函数关系;
(2)求该农户所收获的最大利润.
(总利润=总销售额﹣总承包费用﹣购买板栗苗的费用﹣总管理费用)
21.如图,四边形ABCD中,∠ABC=∠ADC=45°,将△BCD绕点C顺时针旋转一定角度后,点B的对应点恰好与点A重合,得到△ACE.
(1)求证:AE⊥BD;
(2)若AD=2,CD=3,试求出四边形ABCD的对角线BD的长.
22.如图,已知CD是△ABC的角平分线,DE⊥BC,垂足为E,若AC=4,BC=10,△ABC的面积为14,求DE的长.
23.某水果生产基地销售苹果,提供两种购买方式供客户选择
方式1:若客户缴纳1200元会费加盟为生产基地合作单位,则苹果成交价为3元/千克.
方式2:若客户购买数量达到或超过1500千克,则成交价为3.5元/千克;若客户购买数量不足1500千克,则成交价为4元/千克.
设客户购买苹果数量为x(千克),所需费用为y(元).
(1)若客户按方式1购买,请写出y(元)与x(千克)之间的函数表达式;
(备注:按方式购买苹果所需费用=生产基地合作单位会费+苹果成交总价)
(2)如果购买数量超过1500千克,请说明客户选择哪种购买方式更省钱;
(3)若客户甲采用方式1购买,客户乙采用方式2购买,甲、乙共购买苹果5000千克,总费用共计18000元,则客户甲购买了多少千克苹果?
24.勾股定理是数学史上非常重要的一个定理.早在2000多年以前,人们就开始对它进行研究,至今已有几百种证明方法.在欧几里得编的《原本》中证明勾股定理的方法如下,请同学们仔细阅读并解答相关问题:
如图,分别以Rt△ABC的三边为边长,向外作正方形ABDE、BCFG、ACHI.
(1)连接BI、CE,求证:△ABI≌△AEC;
(2)过点B作AC的垂线,交AC于点M,交IH于点N.
①试说明四边形AMNI与正方形ABDE的面积相等;
②请直接写出图中与正方形BCFG的面积相等的四边形.
(3)由第(2)题可得:
正方形ABDE的面积+正方形BCFG的面积= 的面积,即在Rt△ABC中,AB2+BC2= .
25.某公司市场营销部的营销员有部分收入按照业务量或销售额提成,即多卖多得.营销员的月提成收入y(元)与其每月的销售量x(万件)成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题:
(1)求出y(元)与x(万件)(其中x≥0)之间的函数关系式;
(2)已知该公司营销员李平12月份的销售量为1.2万件,求李平12月份的提成收入.
26.如图,Rt△ABC中,∠CAB=90°,∠ACB=30°,D是AB上一点(不与A、B重合),DE⊥BC于E,若P是CD的中点,请判断△PAE的形状,并说明理由.
参考答案与试题解析
一.选择题(共7小题)
1.【解答】解:A、52+42≠62,故不是直角三角形,故不正确;
B、52+32≠62,故不是直角三角形,故不正确;
C、()2+()2=()2,故是直角三角形,故正确;
D、22+()2≠()2,故不是直角三角形,故不正确.
故选:C.
2.【解答】解:①两边及其中一边上的中线对应相等的两个三角形全等,正确;
②如果对应相等两边夹角一种是锐角一种是钝角,那么即使其中一边上的高对应相等,这两个三角形也不全等,错误;
③两边及一角对应相等的两个三角形全等,如SSA不能判定全等,错误;
④有两角及其中一角的角平分线对应相等的两个三角形全等,正确;
故选:B.
3.【解答】解:在OC上截取OE=OD,连接BE,如图所示:
∵OC=2OA=8,
∴OA=4,
∵AC⊥BD,∠OAB=45°,
∴∠AOD=∠BOE=90°,△OAB是等腰直角三角形,
∴OB=OA=4,
∴AC=OA+OC=12,
在△AOD和△BOE中,
,
∴△AOD≌△BOE(SAS),
∴∠ODA=∠OEB,
∵∠OCB=∠ODA,
∴∠OEB=∠ODA=2∠OCB,
∵∠OEB=∠OCB+∠EBC,
∴∠OCB=∠ECB,
∴BE=CE,
设BE=CE=x,则OE=8﹣x,
在Rt△OBE中,由勾股定理得:42+(8﹣x)2=x2,
解得:x=5,
∴CE=5,OD=OE=3,
∴BD=OB+OD=4+3=7,
∵AC⊥BD,
∴四边形ABCD的面积=AC×BD=×12×7=42;
故选:C.
4.【解答】解:∵AB=AC,∠B=32°,
∴∠DAC=2∠B=64°,
∵CD=AB,
∴CA=CD,
∴∠D=∠DAC=64°,
故选:C.
5.【解答】解:∵∠ADC=2∠B,∠ADC=∠B+∠BAD,
∴∠B=∠DAB,
∴DB=DA=,
在Rt△ADC中,
DC===1,
∴BC=+1.
故选:D.
6.【解答】解:添加A选项中条件可用AAS判定两个三角形全等;
添加B选项中条件可用AAS判定两个三角形全等;
添加C选项中条件可用ASA判定两个三角形全等;
添加D选项以后是SSA,无法证明三角形全等;
故选:D.
7.【解答】解:如图所示:
故选:B.
二.填空题(共12小题)
8.【解答】解:∵等腰三角形的一个外角为80°,
∴相邻角为180°﹣80°=100°,
∵三角形的底角不能为钝角,
∴100°角为顶角,
∴底角为:(180°﹣100°)÷2=40°.
故答案为:40.
9.【解答】解:由题意知a﹣3+a+5=0,
解得:a=﹣1,
故答案为:﹣1.
10.【解答】解:∵AC=AD=DB,
∴∠B=∠BAD,∠ADC=∠C,
设∠ADC=α,
∴∠B=∠BAD=,
∵∠BAC=105°,
∴∠DAC=105°﹣,
在△ADC中,
∵∠ADC+∠C+∠DAC=180°,
∴2α+105°﹣=180°,
解得:α=50°.
故答案为:50.
11.【解答】解:∵直角三角形斜边上的中线长为5,
∴直角三角形斜边为10,
∴另一条直角边的长==8.
故答案为:8.
12.【解答】解:∵等腰三角形的周长为12,
∴当2为腰时,它的底长=12﹣2﹣2=8,2+2=4<8,不能构成等腰三角形;
当2为底时,它的腰长=(12﹣2)÷2=5,3+5>5能构成等腰三角形,
即它的另外两边长分别为5和5.
故答案为:5和5.
13.【解答】解:如图所示:
由翻折可知:
AM=A′M=4﹣CM,
∵点A′是BC的中点,
∴A′C=3,
在Rt△A′CM中,根据勾股定理,得
A′M2=A′C2+CM2
(4﹣CM)2=32+CM2
解得CM=.
故答案为.
14.【解答】解:∵线段AB的垂直平分线交AC于点N,
∴NB=NA,
△BCN的周长=BC+CN+BN=7cm,
∴BC+AC=7cm,又AC=4cm,
∴BC=3cm,
故答案为:3.
15.【解答】解:∵AC=AD=DB,
∴∠B=∠BAD,∠ADC=∠C,
设∠ADC=α,
∴∠B=∠BAD=,
∵∠BAC=120°,
∴∠DAC=120°﹣,
在△ADC中,
∵∠ADC+∠C+∠DAC=180°,
∴2α+120°﹣=180°,
解得:α=40°.
∴∠ADC=40°,
故答案为:40°.
16.【解答】解:将△AMB逆时针旋转90°到△ACF,连接NF,
∴CF=BM,AF=AM,∠B=∠ACF.∠2=∠3,
∵△ABC是等腰直角三角形,AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵∠MAN=45°,
∴∠NAF=∠1+∠3=∠1+∠2=90°﹣45°=45°=∠NAF,
在△MAN和△FAN中
∴△MAN≌△FAN(SAS),
∴MN=NF,
∵∠ACF=∠B=45°,∠ACB=45°,
∴∠FCN=90°,
∵CF=BM=1,CN=3,
∴在Rt△CFN中,由勾股定理得:MN=NF==,
故答案为:.
17.【解答】解:∵与(y+4)2互为相反数,
∴+(y+4)2=0,
∴x﹣5=0,y+4=0,
解得x=5,y=﹣4,
∴x+y=5+(﹣4)=1,
∴x+y的平方根为±1.
故答案为:±1.
18.【解答】解:∵分别以△ABC的各边为一边向三角形外部作正方形,这三个正方形的面积分别为6cm2、8cm2、10cm2,
∴三边平方后分别为:6,8,10,
∵6+8≠10,
∴△ABC不是直角三角形.
故答案为:不是.
19.【解答】解:在Rt△ABC中,AC=5,BC=4
∴AB=,
∵EB=AE,BD=AD=,设EB=AE=x,
在Rt△BEC中,∵BE2=BC2+EC2,
∴x2=(5﹣x)2+42,
∴x=4.1;
故答案为:4.1
三.解答题(共7小题)
20.【解答】解:(1)由题意得
y=14x+10(600×15×70%﹣x)+7×600×15×30%﹣(1500+800+80×5)×15
整理得y=4x+41400
故y与x之间的函数关系式为y=4x+41400
(2)∵零售量不高于总销售量的40%
∴x≤600×15×70%×40%
即:x≤2520
又∵4>0,∴对于y=4x+41400而言,y随着x的增大而增大,
∴当x取最大值2520时,y得最大值为51480
答:该农户所收获的最大利润为51480元.
21.【解答】解:(1)如图,设AC与BD的交点为点M,BD与AE的交点为点N,
∵旋转
∴AC=BC,∠DBC=∠CAE
又∵∠ABC=45°,
∴∠ABC=∠BAC=45°,
∴∠ACB=90°,
∵∠DBC+∠BMC=90°
∴∠AMN+∠CAE=90°
∴∠AND=90°
∴AE⊥BD,
(2)如图,连接DE,
∵旋转
∴CD=CE=3,BD=AE,∠DCE=∠ACB=90°
∴DE==3,∠CDE=45°
∵∠ADC=45°
∴∠ADE=90°
∴EA==
∴BD=
22.【解答】解:过点D作DF⊥AC交CA的延长线于点F,如图,
∵CD平分∠ACB,DE⊥BC于E,
∴DF=DE.
∵△ABC的面积为14,
∴S△BCD+S△ACD=14,
∴×DE×10+×DF×4=14,
即5DE+2DE=14,
∴DE=2.
23.【解答】解:(1)y=3x+1200.
(2)按方式1购买时所需费用记作y1元,按方式2购买时所需费用记作y2元,
当x>1500时,y2=3.5x
若y1<y2,则3x+1200<3.5x,解得x>2400.
若y1=y2,则3x+1200=3.5x,解得x=2400.
若y1>y2,则3x+1200>3.5x,解得x<2400.
答:当x>2400时,客户按方式1购买更省钱;当x=2400时,按两种方式购买花钱一样多;
当1500<x<2400时,客户按方式2购买更省钱.
(3)设客户甲购买了x千克苹果.
①若5000﹣x<1500,即x>3500,则由题意得(3x+1200)+4(5000﹣x)=18000,
解得x=3200.经检验,不合题意,舍去.
②若5000﹣x≥1500,即x≤3500,则由题意得(3x+1200)+3.5(5000﹣x)=18000,
解得x=1400.经检验,符合题意.
答:客户甲购买了1400千克苹果.
24.【解答】(1)证明:∵四边形ABDE、四边形ACHI是正方形,
∴AB=AE,AC=AI,∠BAE=∠CAI=90°,
∴∠EAC=∠BAI,
在△ABI和△AEC中,,
∴△ABI≌△AEC(SAS);
(2)①证明:∵BM⊥AC,AI⊥AC,
∴BM∥AI,
∴四边形AMNI的面积=2△ABI的面积,
同理:正方形ABDE的面积=2△AEC的面积,
又∵△ABI≌△AEC,
∴四边形AMNI与正方形ABDE的面积相等.
②解:四边形CMNH与正方形BCFG的面积相等,理由如下:
连接BH,过H作HP⊥BC于P,如图所示:
易证△CPH≌△ABC(AAS),四边形CMNH是矩形,
∴PH=BC,
∵△BCH的面积=CH×NH=BC×PH,
∴CH×NH=BC2,
∴四边形CMNH与正方形BCFG的面积相等;
(3)解:由(2)得:正方形ABDE的面积+正方形BCFG的面积=正方形ACHI的面积;
即在Rt△ABC中,AB2+BC2=AC2;
故答案为:正方形ACHI,AC2.
25.【解答】解:(1)设营业员月提成收入y与每月销售量x的函数关系式为y=kx+b,
将(0,600)、(2,2200)代入,可列方程组
解得
∴y=800x+600(x≥0)
(2)当x=1.2时,y=800×1.2+600=1560;
∴李平12月份的提成收入为1560元.
26.【解答】解:△PAE的形状为等边三角形;理由如下:
∵在Rt△CAD中,∠CAD=90°,P是斜边CD的中点,
∴PA=PC=CD,
∴∠ACD=∠PAC,
∴∠APD=∠ACD+∠PAC=2∠ACD,
同理:在Rt△CED中,PE=PC=CD,∠DPE=2∠DCB,
∴PA=PE,即△PAE是等腰三角形,
∴∠APE=2∠ACB=2×30°=60°,
∴△PAE是等边三角形.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2023/11/销售方式
批发
零售
售价(元/kg)
10
14
相关试卷
这是一份江苏无锡市玉祁高级中学2024-2025学年八上数学第6周阶段性训练试题【含答案】,共27页。试卷主要包含了若,则等内容,欢迎下载使用。
这是一份江苏南通市崇川初级中学2024-2025学年八上数学第8周阶段性训练模拟练习【含答案】,共32页。试卷主要包含了点A等内容,欢迎下载使用。
这是一份江苏淮安市凌桥中学2024-2025学年八上数学第7周阶段性训练模拟练习【含答案】,共17页。试卷主要包含了下列各组数中,是勾股数的是等内容,欢迎下载使用。








