

江苏无锡市玉祁高级中学2024-2025学年九上数学第6周阶段性训练试题【含答案】
展开
这是一份江苏无锡市玉祁高级中学2024-2025学年九上数学第6周阶段性训练试题【含答案】,共23页。
A.k>0B.k>4C.k<0D.k<4
2.如图,C为⊙O上一点,AB是⊙O的直径,AB=4,∠ABC=30°,现将△ABC绕点B按顺时针方向旋转30°后得到△A'BC',BC'交⊙O于点D,则图中阴影部分的面积为( )
A.B.C.D.
3.如图,已知抛物线y=ax2+c与直线y=kx+m交于A(﹣3,y1),B(1,y2)两点,则关于x的不等式ax2+c≥﹣kx+m的解集是( )
A.x≤﹣3或x≥1B.x≤﹣1或x≥3C.﹣3≤x≤1D.﹣1≤x≤3
4.若关于x的一元二次方程x2+x﹣3m+1=0有两个实数根,则m的取值范围是( )
A.mB.mC.mD.m
二.填空题(共12小题)
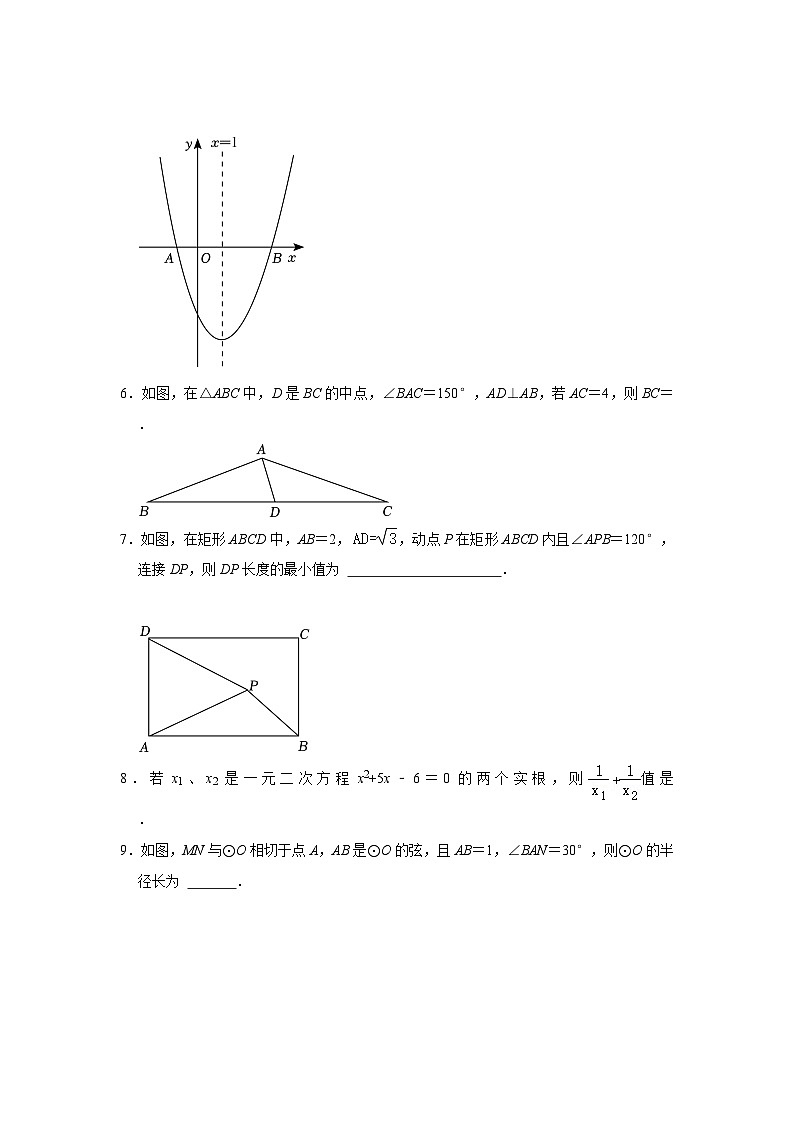
5.如图,抛物线y=x2﹣ax﹣(a+1)(其中a为常数)的对称轴为直线x=1,与x轴交于点A,点B,则AB的长度为 .
6.如图,在△ABC中,D是BC的中点,∠BAC=150°,AD⊥AB,若AC=4,则BC= .
7.如图,在矩形ABCD中,AB=2,,动点P在矩形ABCD内且∠APB=120°,连接DP,则DP长度的最小值为 .
8.若x1、x2是一元二次方程x2+5x﹣6=0的两个实根,则值是 .
9.如图,MN与⊙O相切于点A,AB是⊙O的弦,且AB=1,∠BAN=30°,则⊙O的半径长为 .
10.如图,在四边形ABCD中,点E在AD上,EC∥AB,EB∥DC,若△ABE面积为5,△ECD的面积为1,则△BCE的面积是 .
11.在△ABC中,AB=2,,则∠A度数的最大值为 °.
12.已知抛物线y=x2+bx+c过A(﹣1,0),B(m,0)两点.若2<m<3,则下列四个结论中正确的是 .(请将所有正确结论的序号都填写到横线上):①b>0;②c<0;③点M(x1,y1),N(x2,y2)在抛物线上,若x1<x2,x1+x2=1,则y1>y2;④关于x的一元二次方程x2+bx+c+2=0必有两个不相等的实数根.
13.如图,△ABC∽△ADE,且BC=2DE,则的值为 .
14.设a,b是方程x2+x﹣2022=0的两个实数根,则(a﹣1)(b﹣1)的值为 .
15.如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与点B,C重合),过点C作CN⊥DM交AB于点N,连接OM、ON,MN.下列五个结论:①△CNB≌△DMC;②ON=OM;③ON⊥OM;④若AB=2,则S△OMN的最小值是1;⑤AN2+CM2=MN2.其中正确结论是 ;(只填序号)
16.已知数据x1+1,x2+2,x3+3的平均数是6,那么数据x1,x2,x3的平均数是 .
三.解答题(共8小题)
17.一只不透明的袋子中装有三个乒乓球,球面上分别标有数字1、2、3,这些乒乓球除所标数字不同外其余都相同.
(1)搅匀后从中任意摸出一个乒乓球,摸出的乒乓球的球面上恰好标有数字3的概率为 ;
(2)搅匀后先从袋子中任意摸出一个球,将球面上所标数字作为一个两位数的十位数字,不放回,再从袋中余下的球中任意摸出一个球,将球面上所标数字作为这个两位数的个位数字,求这个两位数恰好是奇数的概率.(请用画树状图或列表等方法说明理由)
18.已知如图,抛物线y=﹣x2+2mx+2m+1(m是常数,且m>0)的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.其对称轴与线段BC交于点E,与x轴交于点F.连接OE,CD.
(1)填空:∠OBC= °;
(2)设h=OC﹣DE,请写出h关于m的函数表达式,并求出h的最大值;
(3)将△OCE沿点C到点D的方向平移,使得点C与点D重合.设点E的对应点为点E',问点E'能否落在二次函数y=﹣x2+2mx+2m+1的图象上?若能,请求出此时m的值;若不能,请说明理由.
19.已知二次函数y=ax2﹣4ax+4的图象与x轴有唯一公共点.
(1)求a的值;
(2)当0≤x≤m时(m>0),函数的最大值为4,且最小值为0,则实数m的取值范围是 .
20.如图,矩形ABCD中,AD=3,CD=4,点P从点A出发,以每秒1个单位长度的速度在射线AB上向右运动,运动时间为t秒,连接DP交AC于点Q.
(1)求证:△DCQ∽△PAQ;
(2)若△ADQ是以AD为腰的等腰三角形,求运动时间t的值.
21.如图,以AB为直径的⊙O经过△ABC的顶点C,AE,BE分别平分∠BAC和∠ABC,AE的延长线交BC于点F,交⊙O于点D,连接BD.
(1)求证:∠CBD=∠BAD;
(2)求证:BD=DE;
(3)若,,求BC的长.
22.在平面直角坐标系中,O为坐标原点,直线y=﹣x+3与x轴交于点B,与y轴交于点C.二次函数y=ax2+2x+c的图象过B,C两点,且与x轴交于另一点A,点M为线段OB上的一个动点(不与端点O,B重合).
(1)求二次函数的表达式;
(2)如图①,过点M作y轴的平行线l交BC于点F,交二次函数y=ax2+2x+c的图象于点E,记△CEF的面积为S1,△BMF的面积为S2,当时,求点E的坐标;
(3)如图②,连接CM,过点M作CM的垂线l1,过点B作BC的垂线l2,l1与l2交于点G,试探究的值是否为定值?若是,请求出的值;若不是,请说明理由.
23.某商店销售一款工艺品,每件的成本是30元,为了合理定价,投放市场进行试销:据市场调查,销售单价是40元时,每天的销售量是80件,而销售单价每提高1元,每天就少售出2件,但要求销售单价不得超过55元.
(1)若销售单价为每件45元,求每天的销售利润;
(2)要使每天销售这种工艺品盈利1200元,那么每件工艺品售价应为多少元?
24.某产品的成本是120元/件,在试销阶段,当产品的售价为x(元/件)时,日销量为(200﹣x)件.
(1)写出用售价x(元/件)表示每日的销售利润y(元)的表达式.
(2)当日销售利润是1500元时,产品的售价是多少?日销量是多少件?
(3)当售价定为多少时,日销售利润最大?最大日销售利润是多少元?
参考答案与试题解析
一.选择题(共4小题)
1.【解答】解:根据题意得Δ=(﹣4)2﹣4×1×(﹣k+4)<0,
解得k<0,
所以k的取值范围为k<0.
故选:C.
2.【解答】解:连接OC,OD,过O作OE⊥BD,
∵AB是⊙O的直径,∠ABC=30°,
∴∠ACB=90°,∠BAC=60°,
∴△AOC是等边三角形,
∵AB=4,
∴OB=2,
∵△ABC绕点B按顺时针方向旋转30°后得到ΔA'BC',
∴∠ABC=∠CBC'=30°,
∴∠DOB=60°,△BOD是等边三角形,
∴∠BOC=120°,OD⊥BC,
∴Rt△OCF≌Rt△DBF(HL),
∴阴影部分的面积为:S扇COD==,
故选:C.
3.【解答】解:∵y=kx+m与y=﹣kx+m的图象关于y轴对称,
∴直线y=﹣kx+m与抛物线y=ax2+c的交点A′、B′与点A、B也关于y轴对称,
如图所示:
∵A(﹣3,y1),B(1,y2),
∴A′(3,y1),B′(﹣1,y2),
根据函数图象得:不等式ax2+c≥﹣kx+m的解集是﹣1≤x≤3,
故选:D.
4.【解答】解:∵关于x的一元二次方程x2+x﹣3m+1=0有两个实数根,
∴Δ=12﹣4×1×(﹣3m+1)≥0,
解得:m≥
故选:C.
二.填空题(共12小题)
5.【解答】解:∵抛物线y=x2﹣ax﹣(a+1)(其中a为常数)的对称轴为直线x=1,
∴﹣=1,
解得:a=2,
∴y=x2﹣2x﹣3,
令y=0,得x2﹣2x﹣3=0,
解得:x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0),
∴AB=3﹣(﹣1)=4;
故答案为:4
6.【解答】解:如图,过点C作CE⊥BA交BA的延长线于点E,
∵AD⊥AB,
∴∠BAD=∠E=90°,
∴AD∥CE,
又∵D是BC的中点,
∴AD是△EBC的中线,
∴AD=,BA=AE,BC=2BD,
∵∠BAC=150°,
∴∠EAC=30°,
∴CE=,
∴AE=CE=2,
∴AD=,BA=AE=2,
∴BD=,
∴BC=2BD=2,
故答案为:2.
7.【解答】解:作△ABP的外接圆⊙O,过点O作OE⊥AB于E,作OF⊥DA交DA的延长线于F,连接OA、OB、OD,OD交⊙O于点P′,
∵∠AP′B=∠APB=120°,
∴当B、P、D共线时,DP的长度最小为DP′的长,∠AOB=120°,
∵OE⊥AB,AB=2,
∴AE=AB=1,∠AOE=60°,
∴∠OAE=30°,
∴OE=,OA=,
∴⊙O的半径为,
∵四边形ABCD是矩形,
∴∠FAE=90°,
∵OE⊥AB,OF⊥DA,
∴四边形AEOF是矩形,
∴OF=AE=1,AF=OE=,
∴DF=AD+AF=+=,
∴OD===,
∴DP′=OD﹣OP′=﹣=,
即DP长度的最小值为.
故答案为:.
8.【解答】解:x1+x2=﹣5,x1x2=﹣6,
所以原式===.
故答案为.
9.【解答】解:连接OA,OB,
∵MN与⊙O相切于点A,
∴∠OAN=90°,
∵∠BAN=30°,
∴∠OAB=∠OAN﹣∠BAN=90°﹣30°=60°,
∵OA=OB,
∴△OAB是等边三角形,
∵AB=1,
∴r=1,
故答案为:1.
10.【解答】解:∵EC∥AB,
∴∠A=∠CED,
∵EB∥DC
∴∠AEB=∠D,
∴△ABE∽△ECD,
∴,
∴,,
∵△ABE以AB为底边的高与△BCE以CE为底的高相等,
∴,
故答案为:
11.【解答】解:由题意可得,画出线段AB,以B为圆心BC为半径画圆即可得到,当C从AB与圆交点处开始运动时∠A逐渐增大,当AC与圆相切时最大,随后逐渐减小,
∴当AC⊥BC时,∠A度数的最大,
此时sinA==,
∴∠A度数的最大值为45°,
故答案为:45.
12.【解答】解:∵抛物线y=x2+bx+c过A(﹣1,0),B(m,0)两点,
∴抛物线的对称轴为直线,
∵2<m<3,
∴﹣1+m>1,
∴b<0,故①错误;
∵抛物线y=x2+bx+c过A(﹣1,0),
∴1﹣b+c=0,
∴b=c+1<0,
∴c<0,故②正确;
∵2<m<3,
∴1<﹣1+m<2,
∴,
即抛物线的对称轴位于直线x=1的左侧,
∵x1<x2,x1+x2=1,
∴点N(x2,y2)距离对称轴比点M(x1,y1)远,
∵抛物线开口向上,
∴y1>y2,故③正确;
∵,b=c+1,
∴b=1﹣m,c=﹣m,
∵x2+bx+c+2=0,
∴Δ=b2﹣4(c+2)=(1﹣m)2﹣4(﹣m+2)=(m+1)2﹣8
∵2<m<3,
∴9<(m+1)2<16,
∴1<(m+1)2﹣8<8,
即Δ>0,
关于x的一元二次方程x2+bx+c+2=0必有两个不相等的实数根,故④正确;
故答案为:②③④.
13.【解答】解:∵△ABC∽△ADE,且BC=2DE,
∴=()2=,
∴==,
故答案为:.
14.【解答】解:∵a,b是方程x2+x﹣2022=0的两个实数根,
∴a+b=﹣1,ab=﹣2022,
∴(a﹣1)(b﹣1)=ab﹣a﹣b+1=ab﹣(a+b)+1=﹣2022﹣(﹣1)+1=﹣2020.
故答案为:﹣2020.
15.【解答】解:①∵正方形ABCD中,CD=BC,∠BCD=90°,
∴∠BCN+∠DCN=90°,
∵CN⊥DM,
∴∠CDM+∠DCN=90°,
∴∠BCN=∠CDM,
在△CNB和△DMC中,
∴△CNB≌△DMC(ASA),
故①正确;
②∵△CNB≌△DMC,
∴CM=BN,
∵四边形ABCD是正方形,
∴∠OCM=∠OBN=45°,OC=OB,
在△OCM和△OBN中,,
∴△OCM≌△OBN(SAS),
∴OM=ON,
故②正确;
③∵△OCM≌△OBN,
∴∠COM=∠BON,
∴∠BOM+∠COM=∠BOM+∠BON,即∠NOM=∠BOC=90°,
∴ON⊥OM;
故③正确;
④∵AB=2,
∴S正方形ABCD=4,
∵△OCM≌△OBN,
∴四边形BMON的面积=△BOC的面积=1,即四边形BMON的面积是定值1,
∴当△MNB的面积最大时,△MNO的面积最小,
设BN=x=CM,则BM=2﹣x,
∴△MNB的面积S=x(2﹣x)=﹣x2+x=﹣(x﹣1)2+,
∴当x=1时,△MNB的面积有最大值,
此时S△OMN的最小值是1﹣=,
故④不正确;
⑤∵AB=BC,CM=BN,
∴BM=AN,
在Rt△BMN中,BM2+BN2=MN2,
∴AN2+CM2=MN2,
故⑤正确;
∴本题正确的结论有:①②③⑤,
故答案为:①②③⑤.
16.【解答】解:∵数据x1+1,x2+2,x3+3的平均数是6,
∴x1,x2,x3的平均数+(1+2+3)的平均数=6,
∴x1,x2,x3的平均数+2=6,
∴数据x1,x2,x3的平均数是4;
故答案为:4.
三.解答题(共8小题)
17.【解答】解:(1)∵球面上分别标有数字1、2、3,
∴搅匀后从中任意摸出一个乒乓球,摸出的乒乓球的球面上恰好标有数字3的概率为,
故答案为:;
(2)画树状图如下:
共有6种等可能的结果,其中这个两位数恰好是奇数的结果有4种,
∴这个两位数恰好是奇数的概率为=.
18.【解答】解:(1)把y=0代入y=﹣x2+2mx+2m+1得:﹣x2+2mx+2m+1=0,
解得:x1=﹣1,x2=2m+1,
∵m>0,
∴2m+1>0,
∴x2>x1,
∵点A在点B的左侧,
∴点A的坐标为(﹣1,0),点B的坐标为(2m+1,0),
∴OB=2m+1,
把x=0代入y=﹣x2+2mx+2m+1得:y=2m+1,
∴点C的坐标为(0,2m+1),
∴OC=2m+1,
∴OB=OC,
∵∠BOC=90°,
∴,
故答案为:45.
(2)抛物线的对称轴为直线,
把x=m代入y=﹣x2+2mx+2m+1得:y=﹣m2+2m2+2m+1=m2+2m+1,
∴点D(m,m2+2m+1),
设直线BC的解析式为y=kx+b,把B(2m+1,0),C(0,2m+1)代入得:,
解得:,
∴直线BC的解析式为y=﹣x+2m+1,
把x=m代入得:y=﹣m+2m+1=m+1,
∴点E(m,m+1),
∴DE=m2+2m+1﹣m﹣1=m2+m,
∵h=OC﹣DE,
∴h=2m+1﹣(m2+m)=﹣m2+m+1=,
∴当时,h有最大值,且最大值为.
(3)∵C(0,2m+1),D(m,m2+2m+1),E(m,m+1),
∴根据平移可知,点E'的横坐标为:m+m=2m,
点E'的纵坐标为:m+1+[m2+2m+1﹣(2m+1)]=m2+m+1,
即点E'(2m,m2+m+1),
当E'在抛物线上时,则﹣(2m)2+2m×2m+2m+1=m2+m+1,
解得:m=1或m=0(舍去).
19.【解答】解:(1)∵二次函数y=ax2﹣4ax+4的图象与x轴有唯一公共点,
∴一元二次方程ax2﹣4ax+4=0的判别式等于0,
∴a≠0,(﹣4a)2﹣4×4a=0,
解得:a=1;
(2)由(1)得,y=x2﹣4x+4=(x﹣2)2,
∴当x=2时,ymin=0,
∵当x=0时,y=4,
∴抛物线上点(0,4)的对称点为(4,4),
∵0≤x≤m时(m>0),函数的最大值为4,且最小值为0,
∴2≤m≤4,
故答案为:2≤m≤4.
20.【解答】(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠DCQ=∠PAQ,
又∵∠DQC=∠PQA,
∴△DCQ∽△PAQ;
(2)解:∵四边形ABCD是矩形,AD=3,CD=4,
∴AC=5,
由题意知,AP=t,,
①当AD=AQ时,即:AQ=3,CQ=2
∵△DCQ∽△PAQ,
∴,即:,解得:t=6;
②当..时,即:DQ=3,
∵△DCQ∽△PAQ,
∴,即:,整理得:,
两边同时平方得:,整理得:,
解得:或t=0(舍去).
综上:△ADQ是以AD为腰的等腰三角形时,t=6或.
21.【解答】(1)证明:∵AE平分∠BAC,
∴∠BAD=∠CAD,
∵∠CBD=∠CAD,
∴∠CBD=∠BAD;
(2)证明:∵AB为⊙O的直径,
∴∠ADB=90°.
∵AE,BE分别平分∠BAC和∠ABC,
∴∠BAE=∠CAE,∠ABE=∠CBE.
∵,
∴∠CAE=∠CBD.
∵∠BED=∠BAE+∠ABE,∠EBD=∠CBD+∠CBE,
∴∠BED=∠EBD,
∴BD=ED;
(3)解:如图,连接OD,交BC于点F.
∵∠BAD=∠CAD,
∴,
∴OD⊥BC,BF=CF.
∵,
∴,
由(2)得△BDE为等腰直角三角形,,
∴BD2+DE2=BE2,
解得:BD=DE=2,
在Rt△OBF中,BF2=OB2﹣OF2,
在Rt△BDF中,,
∴
解得:,
∴,
∴.
22.【解答】解:(1)在一次函数中,
当y=0时,x=3,
当x=0时,y=3,
∴B(3,0),C(0,3),
将B(3,0),C(0,3)代入抛物线得,
解得:,
∴y=﹣x2+2x+3;
(2)如图①,连接OF,设点M坐标为M(m,0),
∵EM∥y轴,
∴点E的坐标为(m,﹣m2+2m+3),点F的坐标为(m,﹣m+3),
由题意可得:S1=S△OME+S△OCE﹣S△COF﹣S△OMF===,,
∵,
∴,
解得:m1=1,(不符合题意舍去),
∴E的坐标为(1,4);
(3)如图②,过G作GN⊥x轴,由题意可得,
∵GM⊥CM,GB⊥CB,GN⊥x轴,∠COB=90°,
∴∠OMC=∠NGM,∠OCM=∠NMG,∠OCB=∠NBG,∠OBC=∠NGB,
∴△COB∽△BNG,△COM∽△MNG,
∴,,
∵B(3,0),C(0,3),
∴BN=CN,OB=OC,
∵CG2=CM2+GM2,
∴,
设点G坐标为G(t+3,t),点M坐标为M(m,0),
可得,
解得:t=m,
∴,
∴,
∴.
23.【解答】解:(1)(45﹣30)×[80﹣(45﹣40)×2]=1050(元).
答:每天的销售利润为1050元.
(2)设每件工艺品售价为x元,则每天的销售量是[80﹣2(x﹣40)]件,
依题意,得:(x﹣30)[80﹣2(x﹣40)]=1200,
整理,得:x2﹣110x+3000=0,
解得:x1=50,x2=60(不符合题意,舍去).
答:每件工艺品售价应为50元.
24.【解答】解:(1)由题意得:y=(200﹣x)(x﹣120)=﹣x2+320x﹣24000;
(2)由题意得:﹣x2+320x﹣24000=1500,解得x=170或150,
y=200﹣x=30或50,
即当日销售利润是1500元时,产品的售价170元/件或150元/件时,相应的日销量是30件或50件;
(3)由题意得:y=(200﹣x)(x﹣120)=﹣(x﹣200)(x﹣120),
∵﹣1<0,故当x=(200+120)=160(元/件)时,y有最大值,最大值为1600(元),
即当定价为160元/件时,最大日销售利润是1600元.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2023/10/14 17:19:57;用户:刘玉松;邮箱:abrahamhenry@sina.cm;学号:4631247
相关试卷
这是一份江苏无锡市玉祁高级中学2024-2025学年八上数学第一次月考试卷【含答案】,共30页。试卷主要包含了已知,如图,已知△ABC,下列说法正确的是等内容,欢迎下载使用。
这是一份江苏无锡市玉祁高级中学2024-2025学年八上数学第6周阶段性训练试题【含答案】,共27页。试卷主要包含了若,则等内容,欢迎下载使用。
这是一份江苏无锡市玉祁高级中学2024-2025学年九上数学上第一次月考试卷【含答案】,共25页。试卷主要包含了如图,反比例函数y=,如图,已知关于x的一元二次方程等内容,欢迎下载使用。









