江苏省杭州市2023-2024学年八年级上学期期中数学模拟试卷

这是一份江苏省杭州市2023-2024学年八年级上学期期中数学模拟试卷，共18页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
1.3的平方根是( )
A. 3或B. 3C. D. 或
2.以下列各组数为边长，能构成直角三角形的是( )
A. 2，3，4B. 3，4，5C. 4，5，6D. 5，6，7
3.如图，≌，若，，则的度数为( )
A.
B.
C.
D.
4.如图，用直尺和圆规作一个角的平分线，是运用了“全等三角形的对应角相等”这一性质，由作图所得条件，判定三角形全等运用的方法是( )
A. SASB. ASAC. AASD. SSS
5.下列各式中计算正确的是( )
A. B. C. D.
6.在下列结论中：
①有一个外角是的等腰三角形是等边三角形；
②有两个外角相等的等腰三角形是等边三角形；
③有一边上的高也是这边上的中线的等腰三角形是等边三角形；
④三个外角都相等的三角形是等边三角形．
其中正确的个数是( )
A. 4个B. 3个C. 2个D. 1个
7.下列说法中：①3的平方根是；②是9的一个平方根；③的平方根是；④的算术平方根是；⑤；⑥的立方根是2；其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
8.如图矩形ABCD的边AD长为2，AB长为1，点A在数轴上对应的点是，以A点为圆心，对角线AC长为半径画弧，交数轴于点E，点E表示的实数是( )
A. B. C. D.
9.如图钢架中，，焊上等长的钢条，，，……来加固钢架.若，且恰好用了3根钢条，则下列各数中哪个可能是的值( )
A. B. C. D.
10.如图，在中，已知，于点M，于点N，P为BC边的中点，连接PM，PN，则下列结论：①；②；③为等边三角形；④当时，，其中正确的是( )
A. ①②B. ①②③C. ①②④D. ①②③④
二、填空题：本题共6小题，每小题3分，共18分。
11.如图，一名工作人员不慎将一块三角形模具打碎成三块，他要带其中一块或两块碎片到商店去配一块与原来一样的三角形模具，他带______去最省事.
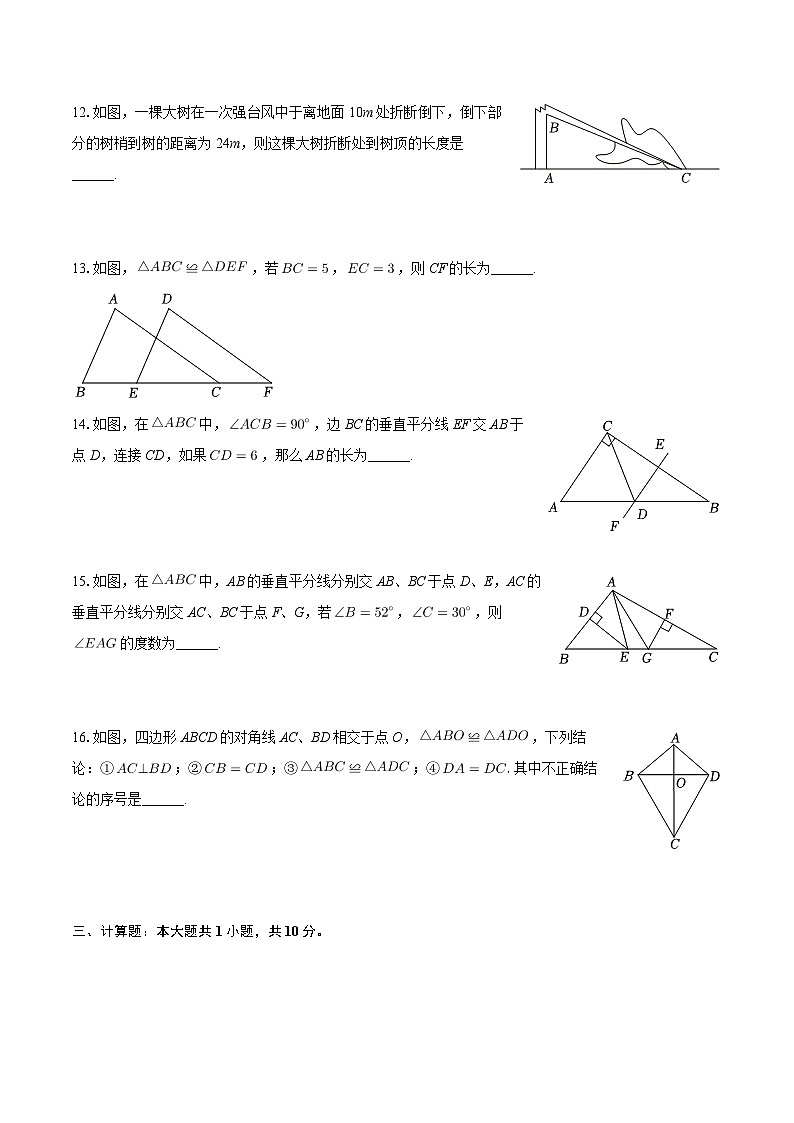
12.如图，一棵大树在一次强台风中于离地面10m处折断倒下，倒下部分的树梢到树的距离为24m，则这棵大树折断处到树顶的长度是______.
13.如图，≌，若，，则CF的长为______.
14.如图，在中，，边BC的垂直平分线EF交AB于点D，连接CD，如果，那么AB的长为______.
15.如图，在中，AB的垂直平分线分别交AB、BC于点D、E，AC的垂直平分线分别交AC、BC于点F、G，若，，则的度数为______.
16.如图，四边形ABCD的对角线AC、BD相交于点O，≌，下列结论：①；②；③≌；④其中不正确结论的序号是______.
三、计算题：本大题共1小题，共10分。
17.已知：如图，将矩形纸片ABCD沿对角线BD对折，点C落在点E的位置，AD与BE相交于点
求证：是等腰三角形；
若，，求BF的长．
四、解答题：本题共7小题，共62分。解答应写出文字说明，证明过程或演算步骤。
18.本小题8分
如图，点A、B、C、D在一条直线上，且，，求证：
19.本小题8分
如图，四边形ABCD中，，，，，，求四边形ABCD的面积．
20.本小题8分
如图，在中，，，D为BC的中点，
求AD长；
若，，垂足为E、F，求证：
21.本小题8分
如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
在图中画出与关于直线l成轴对称的
的面积为______.
在直线l上找一点在答题纸上图中标出，使的长最短．
22.本小题10分
“儿童散学归来早，忙趁东风放纸鸢”．又到了放风筝的最佳时节．某校八年级班的小明和小亮学习了“勾股定理”之后，为了测得风筝的垂直高度CE，他们进行了如下操作：①测得水平距离BD的长为15米；②根据手中剩余线的长度计算出风筝线BC的长为25米；③牵线放风筝的小明的身高为米．
求风筝的垂直高度CE；
如果小明想风筝沿CD方向下降12米，则他应该往回收线多少米？
23.本小题10分
如图，点B、F、C、E在一条直线上点F、C之间不能直接测量，点A、D在直线l的异侧，测得，，，若，，求FC的长度．
24.本小题10分
如图，和都是等腰三角形，BC、DE分别是这两个等腰三角形的底边，且
求证：；
连接DC，若，试说明：AD平分
答案和解析
1.【答案】D
【解析】解：3的平方根是
故选：
利用平方根定义计算即可．
此题考查平方根，熟练掌握平方根的定义是解本题的关键．
2.【答案】B
【解析】解：A、，不能构成直角三角形，故本选项不符合题意；
B、，能构成直角三角形，故本选项符合题意；
C、，不能构成直角三角形，故本选项不符合题意；
D、，不能构成直角三角形，故本选项不符合题意．
故选：
根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个三角形是直角三角形．如果没有这种关系，这个就不是直角三角形，逐一判定即可．
本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．
3.【答案】D
【解析】解：≌，，
，
，
，
故选：
根据全等三角形对应角相等可得，再根据三角形的内角和定理列式求出
本题考查了全等三角形的性质和三角形内角和定理的应用，注意：全等三角形的对应角相等，对应边相等．
4.【答案】D
【解析】解：用直尺和圆规作一个角的平分线，是运用了“全等三角形的对应角相等”这一性质，
由作图所得条件，判定三角形全等运用的方法是：由得出≌
故选：
根据作图过程可知用到的三角形全等的判定方法是
此题主要考查了基本作图，解题关键是掌握作角平分线的依据．
5.【答案】B
【解析】解：A、，原计算错误，故此选项不符合题意；
B、，原计算正确，故此选项符合题意；
C、，原计算错误，故此选项不符合题意；
D、，原计算错误，故此选项不符合题意．
故选：
利用算术平方根和平方根的定义逐项进行判断即可得到正确的答案．
本题考查了平方根与算术平方根．解题的关键是掌握平方根与算术平方根的定义，要注意一个正数的平方根有两个，它们互为相反数．
6.【答案】C
【解析】【分析】
本题主要考查等边三角形的判定，熟练掌握等边三角形的判定方法是解题的关键．
根据三角形的判定方法，逐一进行分析判断即可得解．
【解答】
解：①有一个外角是的等腰三角形，即有一个内角是，由此可判断其为等边三角形，故①正确；
②有两个外角相等的等腰三角形不一定是等边三角形，如果这两个外角是等腰三角形两腰的外角，则这个三角形是等腰三角形，故②错误；
③有一边上的高也是这边上的中线的等腰三角形不一定是等边三角形，故③错误；
④三个外角都相等的三角形其三个内角相等，是等边三角形，故④正确，
综上可知，正确的有①④共2个．
故选
7.【答案】C
【解析】解：①3的平方根是；
②是9的一个平方根；
③的平方根是；
④的算术平方根是；
⑤；
⑥的立方根是；
综上：说法正确的有②③④，
故选：
根据平方根和立方根的定义和运算法则对选项逐一判断即可．
本题考查了平方根，算术平方根，立方根的相关知识，解题关键在于区别平方根和算术平方根的概念．
8.【答案】B
【解析】解：如图所示：连接AC，
由题意可得：，
则点E表示的实数是：
故选：
直接利用勾股定理得出AC的长，进而得出点E表示的实数．
此题主要考查了实数与数轴，正确得出AC的长是解题关键．
9.【答案】B
【解析】解：，，，，
，，，，
，
要使得这样的钢条只能焊上4根，
，
由题意，
故选：
根据等腰三角形的性质可得到几组相等的角，再根据三角形外角的性质可得到与之间的关系，从而不难求解．
此题主要考查等腰三角形的性质，三角形外角的性质及三角形内角和定理，熟练掌握等腰三角形的性质是解题的关键．
10.【答案】D
【解析】解：①于点N，P为BC边的中点，
，
正确，故①正确；
②于点M，于点N，P为BC边的中点，
，，
，故②正确；
③，于点M，于点N，
，
在中，，
点P是BC的中点，，，
，
，，
，
，
是等边三角形，故③正确；
④当时，于点N，
，，
，
为BC边的中点，
，为等腰直角三角形，
，故④正确．
故选：
根据直角三角形斜边上的中线等于斜边的一半可判断①②正确；
先根据直角三角形两锐角互余的性质求出，再根据三角形的内角和定理求出，然后根据三角形的一个外角等于与它不相邻的两个内角的和求出，从而得到，又由①得，根据有一个角是的等腰三角形是等边三角形可判断③正确；
当时，，由P为BC边的中点，得出，判断④正确．
本题主要考查了相似三角形的判定和性质，直角三角形角所对的直角边等于斜边的一半的性质，等边三角形、等腰直角三角形的判定与性质，等腰三角形三线合一的性质，仔细分析图形并熟练掌握性质是解题的关键．
11.【答案】③
【解析】解：由图形可知，③有完整的两角与夹边，根据“角边角”可以作出与原三角形全等的三角形，
所以，最省事的做法是带③去．
故答案为：③．
根据全等三角形的判定方法“角边角”可以判定应当带③去．
本题考查了全等三角形的判定方法，正确理解“角边角”的内容是解题的关键．
12.【答案】26m
【解析】解：是直角三角形，，，
故答案为：
根据勾股定理求出大树折断部分的高度即可求解．
本题考查的是勾股定理的应用，解答此题的关键是先根据勾股定理求出BC的长度．
13.【答案】2
【解析】解：≌，
，
，
，
故答案为：
利用全等三角形的性质可得，然后利用等式性质求得答案即可．
此题主要考查了全等三角形的性质，关键是掌握全等三角形的对应边相等．
14.【答案】12
【解析】解：因为EF是边BC的垂直平分线，，
所以，
所以，
因为，，
所以，
所以，
所以，
故答案为：
根据线段的垂直平分线的性质得到，则，由，得，从而，，则便可求出．
本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
15.【答案】
【解析】解：，，
，
是AB的垂直平分线，
，
，
同理可得：，
，
，
故答案为：
根据三角形内角和定理求出，根据线段垂直平分线的性质得到，，根据等腰三角形的性质得到，，再进一步解答即可．
本题主要是考查了三角形内角和、垂直平分线以及等腰三角形的性质，熟练应用三角形内角和与等腰三角形的性质求解角的度数，利用垂直平分线证边相等，是解决本题的关键．
16.【答案】④
【解析】解：≌，
，，，，
，故①正确；
四边形ABCD的对角线AC、BD相交于点O，
，
在和中，，
≌，故③正确；
，故②正确．
，
故④不正确；
故答案为：④．
根据全等三角形的性质得出，，，，再根据全等三角形的判定定理得出≌，进而得出其它结论．
本题考查了全等三角形的判定和性质、线段垂直平分线的性质、等腰三角形的性质等知识；掌握全等三角形的判定与性质是解题的关键．
17.【答案】解：由折叠可知，
，
，
，
，
是等腰三角形．
设，则，，
在中，根据勾股定理有
解得：，
的长为
【解析】证明，得出，则结论得证；
设，则，，在中，根据勾股定理有，解方程即可得解．
本题考查的是翻折变换，矩形的性质，勾股定理，熟知图形翻折不变性的性质是解答此题的关键．
18.【答案】证明：，
，
，
在和中，
，
≌，

【解析】利用“SSS”证明≌，然后根据全等三角形的性质即可证明
本题主要考查了全等三角形的判定与性质，解题关键是熟练掌握常用的全等三角形判定方法．
19.【答案】解：连接AC，
，，，
，
，，
，，
，
是直角三角形，
，
四边形ABCD的面积的面积的面积
，
四边形ABCD的面积为
【解析】连接AC，在中，利用勾股定理求出，然后利用勾股定理的逆定理证明是直角三角形，从而可得，最后再利用四边形ABCD的面积的面积的面积，进行计算即可解答．
本题考查了勾股定理，勾股定理的逆定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
20.【答案】解：如图，连接AD，
为BC的中点，，
，
又，
，
在中，由勾股定理得，
；
证明：，，
是等腰的角平分线，
又，，

【解析】连接AD，根据等腰三角形的性质可得，再利用勾股定理即可；
利用等腰三角形的性质得AD是等腰的角平分线，再根据角平分线的性质即可证明结论．
本题考查了等腰三角形的性质，勾股定理，角平分线的性质，熟练掌握勾股定理以及角平分线的性质是解题的关键．
21.【答案】解：如图所示，即为所求；
；
连接，交l于P，点P即为所求．
【解析】【分析】
首先确定A、B、C三点关于l轴的对称点位置，再连接即可；
利用矩形面积减去周围多余三角形的面积即可；
连接，于直线l的交点就是p点位置．
此题主要考查了作图--轴对称变换，关键是正确确定组成图形的关键点关于对称轴的对称点位置．
【解答】
解：见答案；
，
故答案为；
见答案．
22.【答案】解：在中，
由勾股定理得，，
所以，米，
所以，米，
答：风筝的高度CE为米.
如下图所示：
由题意得，米，
米，
，即米，
米，
他应该往回收线8米．
【解析】本题考查了勾股定理的应用，熟悉勾股定理，能从实际问题中抽象出勾股定理是解题的关键．
利用勾股定理求出CD的长，再加上DE的长度，即可求出CE的高度；
根据勾股定理即可得到结论
23.【答案】解：，
，
，
，
在与中，
，
≌，
，
，
，
，，

【解析】先证明，再根据ASA即可证明≌，根据全等三角形的性质即可解答．
本题考查全等三角形的判定和性质、平行线的判定等知识，解题的关键是正确寻找全等三角形的条件，记住平行线的判定方法．
24.【答案】证明：和都是等腰三角形，BC、DE分别是这两个等腰三角形的底边，
，，
，
，
，
在和中，
，
≌，
解：连接CD，
，，
，
在和中，
，
≌，
，
平分
【解析】由，推导出，即可根据全等三角形的判定定理“SAS”证明≌，得；
由全等三角形的判定定理“SSS”证明≌，得，则AD平分
此题重点考查等腰三角形的性质、全等三角形的判定与性质等知识，证明≌及≌是解题的关键．