江苏省扬州市2023-2024学年八年级上学期期末数学模拟试卷(含答案)

这是一份江苏省扬州市2023-2024学年八年级上学期期末数学模拟试卷(含答案)，共33页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题。（本大题共8小题，每小题3分，共24分．在每小题给出的四个选项中，只有一项是符合题目要求的，请将选择题的答案用2B铅笔涂在答题卡相对应的位置上．）
1．视力表中的字母“E”有各种不同的摆放形式，下面各种组合中的两个字母“E”不能关于某条直线成轴对称的是（ ）
A．B．C．D．
2．满足下列条件的中，不是直角三角形的是（ ）
A．B．
C．D．
3．若，是两个连续的整数且，则（ ）
A．8B．7C．6D．5
4．下列各点中，不在函数的图象上的是（ ）
A．B．C．D．
5．下图中全等的两个三角形是（ ）
A．①②B．②③C．①④D．③④
6．信息课上，小文同学利用计算机软件绘制了美丽的蝴蝶，如图，在绘图过程中，小文建立平面直角坐标系，先画出一半图形，利用对称性画出另一半．若图中点A的坐标为，则其关于y轴对称的点B的坐标为（ ）
A．B．C．D．
第6题第7题
7．如图，在中，以点为圆心、长为半径作圆弧交于点，再分别以点和点为圆心，大于长为半径作圆弧，两弧分别交于点和点，连结交于点，若的周长为，，则的长为（ ）
A．4B．8C．9D．10
8．如图，是等边三角形，D是线段上一点（不与点B，C重合），连接，点E，F分别在线段，的延长线上，且，点D从B运动到C的过程中，周长的变化规律是（ ）
A．先变小后变大B．先变大后变小C．一直变小D．不变
二、填空题。（本大题共10小题，每小题3分，共30分．把答案直接填在答题卡相对应的位置上）
9．比较大小： 4．（填“>”“<”或“=”）
10．等腰三角形一腰上的高与另一腰所成的角为，则顶角的度数为 .
11．正方形的对角线长为，则它的周长为 ．
12．如图，，，，，是内的一条射线，且，P为上一动点，则的最大值是 ．（结果表示根据需要可以含a，b，c）
第12题
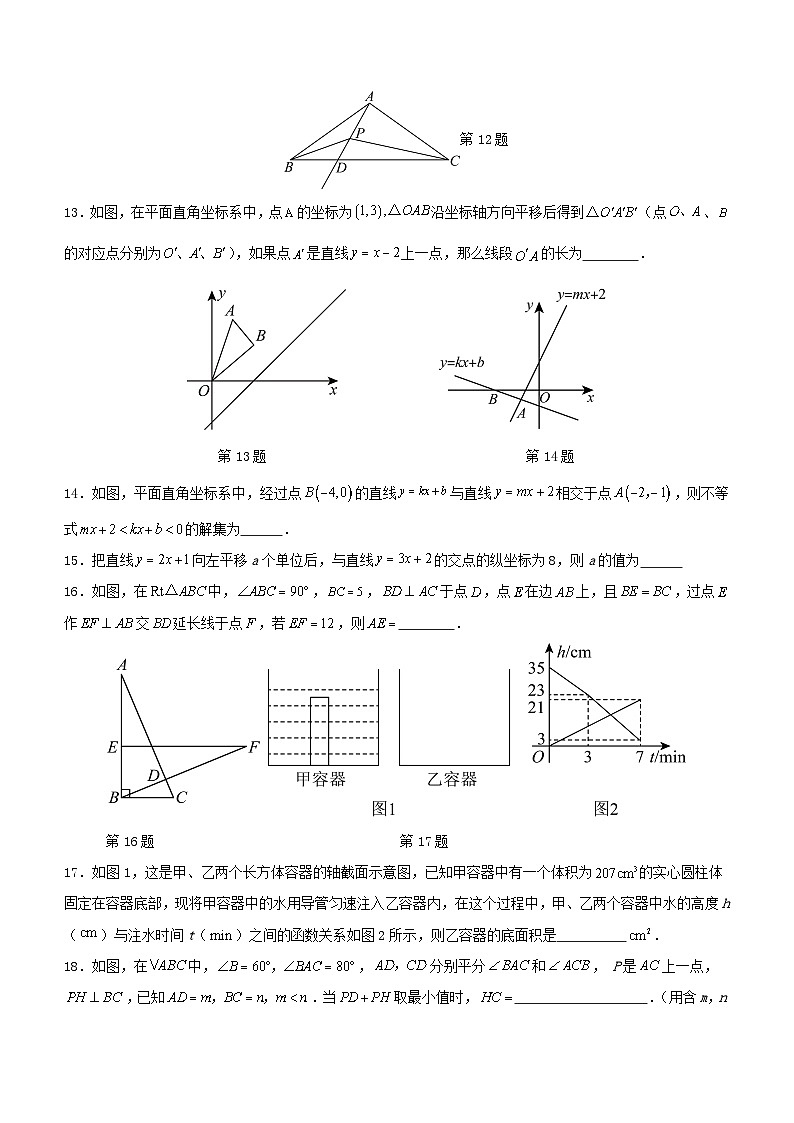
13．如图，在平面直角坐标系中，点的坐标为沿坐标轴方向平移后得到（点、的对应点分别为），如果点是直线上一点，那么线段的长为 ．
第13题第14题
14．如图，平面直角坐标系中，经过点的直线与直线相交于点，则不等式的解集为 ．
15．把直线向左平移a个单位后，与直线的交点的纵坐标为8，则a的值为
16．如图，在中，，，于点，点在边上，且，过点作交延长线于点，若，则 ．

第16题 第17题
17．如图1，这是甲、乙两个长方体容器的轴截面示意图，已知甲容器中有一个体积为的实心圆柱体固定在容器底部，现将甲容器中的水用导管匀速注入乙容器内，在这个过程中，甲、乙两个容器中水的高度h（）与注水时间t（）之间的函数关系如图2所示，则乙容器的底面积是 ．
18．如图，在中，，分别平分和， P是上一点，，已知．当取最小值时， ．（用含m，n的式子表示）
第18题
三、解答题。（本大题共10小题，共96分，把解答过程写在答题卡相应的位置上．解答时应写出必要的计算过程、推演步骤或文字说明，作图时用黑色墨水签字笔）
19．（8分）
(1)计算：(2)求出式子中x的值：
20．（8分）如图，在中，，，D为BC边上一点，于点E，若，求的面积．
21．（8分）已知在平面直角坐标系中有三点，，，请回答如下问题：
(1)在坐标系内描出点A、B、C的位置，连接，，；判断的形状是 _____；
(2)求出以A、B、C三点为顶点的三角形的面积；
(3)在y轴上是否存在点P，使以A、B、P三点为顶点的三角形的面积为，若存在，请直接写出点P的坐标；若不存在，请说明理由．
22．（8分）已知：在四边形中，，．
(1)求的长．
(2)是直角三角形吗？如果是，请说明理由．
(3)求这块空地的面积．
23．（8分）已知一次函数的图象分别交轴，轴于、两点．
(1)求出交点、的坐标；
(2)请在平面直角坐标系中画出函数的图象；
(3)若点坐标为，求的面积．
24．（10分）如图，在中，已知，，，直线，动点从点开始沿射线方向以每秒2厘米的速度运动，动点也同时从点开始在直线上以每秒1厘米的速度运动，连结，设运动时间为秒．
(1)求的长：
(2)当为多少时，的面积为．
(3)当为多少时，，并简要说明理由（可在备用图中画出具体图形）．
25．（10分）如图，是一种学生双肩背包，其背带由固定带、活动带和调节扣构成．使用时，可以通过调节调节扣使背带的总长度（固定带与活动带使用部分的长度总和，其中调节扣所占的长度忽略不计）加长或缩短．设活动带未使用部分的长度为xcm，背带的总长度为ycm，经测量，得到如下数据：（说明：本题只讨论一条背带）
(1)根据表中数据的规律，填空：__________，__________．
(2)当时，求关于的函数解析式．
(3)在上面的平面直角坐标系中，请直接画出（2）中的函数图象；
(4)根据小敏的身高和习惯，背带的总长度为时，背起来最合适，请求出此时活动带未使用部分的长度．
26．（12分）如图1，在长方形中，，有一只蚂蚁从点处开始以每秒1个单位的速度沿边向点爬行，另一只蚂蚁从点以每秒1个单位的速度沿边向点爬行，蚂蚁的大小忽略不计，如果同时出发，设运动时间为秒．
(1)当时，的面积是______；
(2)如图2，当是以为底的等腰三角形时，求的值；
(3)当同时运动3秒时，点停止运动，点立即以原速向点返回，在返回的过程中，是否存在点，使得平分？若存在，求出点运动的时间，若不存在，请说明理由．
27．（12分）如图，在下列带有坐标系的网格中，△ABC的顶点都在边长为1的小正方形的顶点上，A（﹣3，3），B（﹣4，﹣2），C（0，﹣1）．
（1）直接写出△ABC的面积为 ；
（2）画出△ABC关于y轴的对称的△DEC（点D与点A对应，点E与点B对应），点E的坐标为 ；
（3）用无刻度的直尺，运用所学的知识作图（保留作图痕迹）．
①作出△ABC的高线AF
②在边BC上确定一点P，使得∠CAP＝45°．
28．（12分）如图，在平面直角坐标系内，有一个等腰．
（1）如图1，点，点，点C的坐标为________．
（2）如图2，点，点B在y轴负半轴上，点C在第一象限，过点C作垂直于x轴于点H，则的值为___________．
（3）如图3，点B与原点重合，点A在x轴负半轴上，点C在y轴正半轴上，点D为x轴正半轴上一点，点M为线段中点，在y轴正半轴上取点E，使，过点D作，交的延长线于点F，请补全图形，判断与的数量关系，并证明你的结论．
答案
一、选择题。（本大题共8小题，每小题3分，共24分．在每小题给出的四个选项中，只有一项是符合题目要求的，请将选择题的答案用2B铅笔涂在答题卡相对应的位置上．）
1．视力表中的字母“E”有各种不同的摆放形式，下面各种组合中的两个字母“E”不能关于某条直线成轴对称的是（ ）
A．B．C．D．
答案：A
2．满足下列条件的中，不是直角三角形的是（ ）
A．B．
C．D．
答案：B
故选：B．
3．若，是两个连续的整数且，则（ ）
A．8B．7C．6D．5
答案：B
4．下列各点中，不在函数的图象上的是（ ）
A．B．C．D．
答案：C
5．下图中全等的两个三角形是（ ）
A．①②B．②③C．①④D．③④
答案：A
6．信息课上，小文同学利用计算机软件绘制了美丽的蝴蝶，如图，在绘图过程中，小文建立平面直角坐标系，先画出一半图形，利用对称性画出另一半．若图中点A的坐标为，则其关于y轴对称的点B的坐标为（ ）
A．B．C．D．
答案：A
7．如图，在中，以点为圆心、长为半径作圆弧交于点，再分别以点和点为圆心，大于长为半径作圆弧，两弧分别交于点和点，连结交于点，若的周长为，，则的长为（ ）
A．4B．8C．9D．10
答案：B
8．如图，是等边三角形，D是线段上一点（不与点B，C重合），连接，点E，F分别在线段，的延长线上，且，点D从B运动到C的过程中，周长的变化规律是（ ）
A．先变小后变大B．先变大后变小C．一直变小D．不变
答案：A
二、填空题。（本大题共10小题，每小题3分，共30分．把答案直接填在答题卡相对应的位置上）
9．比较大小： 4．（填“>”“<”或“=”）
答案：>
10．等腰三角形一腰上的高与另一腰所成的角为，则顶角的度数为 .
答案：或/或
11．正方形的对角线长为，则它的周长为 ．
答案：8
12．如图，，，，，是内的一条射线，且，P为上一动点，则的最大值是 ．（结果表示根据需要可以含a，b，c）
答案：a
解：如图，
作点关于射线的对称点，连接、，．
则，，，．
∵，
∴，
∴ 是等边三角形，
∴，
在中，，
当、、在同一直线上时，取最大值，即为a．
∴的最大值是a．
13．如图，在平面直角坐标系中，点的坐标为沿坐标轴方向平移后得到（点、的对应点分别为），如果点是直线上一点，那么线段的长为 ．
答案：或/和
解：点，沿轴平移到，点与点对应，
∴设当，即沿轴向右平移，且点是直线上一点，
∴，解得，，
∴沿轴向右平移个单位长度到，如图所示，过点作轴于点，连接，

∴，
∴，，
在中，；
设当，即沿轴向下平移，且点是直线上一点，
∴， 即，
∴沿轴向下平移个单位长度到，如图所示，过点作轴于点，连接，

∴，
∴，，
在中，；
综上所述，线段的长为或，
故答案为：或．
14．如图，平面直角坐标系中，经过点的直线与直线相交于点，则不等式的解集为 ．
答案：/
解：经过点的直线与直线相交于点，
不等式的解集为．
故答案为：．
15．把直线向左平移a个单位后，与直线的交点的纵坐标为8，则a的值为
答案：
解：∵直线向左平移a个单位，
∴
∵把直线向左平移a个单位后，与直线的交点的纵坐标为8，
∴把代入，得，即交点的坐标为
故把代入
得
解得，
故答案为：
16．如图，在中，，，于点，点在边上，且，过点作交延长线于点，若，则 ．
答案：7
解：∵，
∴，
∵，
∴，
∴，，
∴，
在和中
，
∴．
∴．
∵，
∴．
故答案为：7．
17．如图1，这是甲、乙两个长方体容器的轴截面示意图，已知甲容器中有一个体积为的实心圆柱体固定在容器底部，现将甲容器中的水用导管匀速注入乙容器内，在这个过程中，甲、乙两个容器中水的高度h（）与注水时间t（）之间的函数关系如图2所示，则乙容器的底面积是 ．
答案：60
解：设甲容器底面积为，乙容器底面积为，
根据图象可知，拐点
∴实心铁柱的高为，
∴实心铁柱的底面积为，
甲容器的高度与时间的函数图象分为2段，
，函数图象过点，
可得函数解析式为，
，函数图象过点，
可得函数解析式为，
乙容器的高度与时间的图象经过点，，
∴，
当时，，
，，
∴，
，
∵，
∴，
故答案为：60．
18．如图，在中，，分别平分和， P是上一点，，已知．当取最小值时， ．（用含m，n的式子表示）
答案：
解：∵，
∴，
∵分别平分和，
∴，，
如图，作关于的对称点，连接，，，
∴，，
∴当三点共线时，和最小，
如图，过作于，交于，则是和的最小值，
由对称的性质可得，，，
∴，，
∴是等边三角形，
∴，，
∴是等边三角形，
∴，，
∴，
∴，故答案为：．
三、解答题。（本大题共10小题，共96分，把解答过程写在答题卡相应的位置上．解答时应写出必要的计算过程、推演步骤或文字说明，作图时用黑色墨水签字笔）
19．（8分）
(1)计算：(2)求出式子中x的值：
答案：(1)
(2)或
（1）解；原式
；
（2）解：∵，
∴，
∴，
∴或．
20．（8分）如图，在中，，，D为BC边上一点，于点E，若，求的面积．
答案：．
解：延长，过B点作于点M，
∵，
∴，
∵，，
∴，
∴，
∴．
21．（8分）已知在平面直角坐标系中有三点，，，请回答如下问题：
(1)在坐标系内描出点A、B、C的位置，连接，，；判断的形状是 _____；
(2)求出以A、B、C三点为顶点的三角形的面积；
(3)在y轴上是否存在点P，使以A、B、P三点为顶点的三角形的面积为，若存在，请直接写出点P的坐标；若不存在，请说明理由．
答案：(1)见解析，直角三角形
(2)5
(3)存在，P点的坐标为或
（1）解：A、B、C的位置如图所示：
∵，，
∴，
∴，
∴是直角三角形，
故答案为：直角三角形；
（2）解：依题意，得轴，
∵，，，
∴，
∴；
（3）解：存在，
∵，，
∴P点到的距离为4，
又点P在y轴上，
∴P点的坐标为或．
22．（8分）已知：在四边形中，，．
(1)求的长．
(2)是直角三角形吗？如果是，请说明理由．
(3)求这块空地的面积．
答案：(1)
(2)是直角三角形，理由见解析
(3)
（1）解：在中，，
∴．
（2）解：结论：是直角三角形．
理由：∵，
∴，，
∴，
∴，
∴是直角三角形．
（3）
23．（8分）已知一次函数的图象分别交轴，轴于、两点．
(1)求出交点、的坐标；
(2)请在平面直角坐标系中画出函数的图象；
(3)若点坐标为，求的面积．
答案：(1)点的坐标是，点的坐标是；
(2)见解析；
(3)．
（1）把，代入中，可得：，
∴点的坐标是；
把代入中，可得：，
∴点的坐标是；
（2）在坐标系里描，两点，连接即可，
∴一次函数的图象如图：

（3）设与轴的交点为，设直线的解析式为，
把代入得，，
解得：，
∴直线为，
令，则，
∴，
∴，
∴．
24．（10分）如图，在中，已知，，，直线，动点从点开始沿射线方向以每秒2厘米的速度运动，动点也同时从点开始在直线上以每秒1厘米的速度运动，连结，设运动时间为秒．
(1)求的长：
(2)当为多少时，的面积为．
(3)当为多少时，，并简要说明理由（可在备用图中画出具体图形）．
答案：(1)
(2)当为4或8秒时，的面积为
(3)当为4或12时，
（1）解：∵中，，，，
∴；
（2）解：过A作于F，

∵中，，，
∴，
∵的面积为，
∴，则，
当点D在B的右侧时，，
则（秒）；
当点D在B的左侧时，，
则（秒），
综上，当为4或8秒时，的面积为；
（3）解：∵，
∴，，，
当点E在射线上时，则点D在点B右侧，如图，

由题意，，，
由得，∴；
当点E在射线的反向延长线上时，则点D在点B的左侧，如图，

由题意，，，
由得，∴，
综上，当为4或12时，．
25．（10分）如图，是一种学生双肩背包，其背带由固定带、活动带和调节扣构成．使用时，可以通过调节调节扣使背带的总长度（固定带与活动带使用部分的长度总和，其中调节扣所占的长度忽略不计）加长或缩短．设活动带未使用部分的长度为xcm，背带的总长度为ycm，经测量，得到如下数据：（说明：本题只讨论一条背带）
(1)根据表中数据的规律，填空：__________，__________．
(2)当时，求关于的函数解析式．
(3)在上面的平面直角坐标系中，请直接画出（2）中的函数图象；
(4)根据小敏的身高和习惯，背带的总长度为时，背起来最合适，请求出此时活动带未使用部分的长度．
答案：(1)，
(2)
(3)见解析
(4)
（1）根据解活动带未使用部分的长度每增加，背带的总长度将减小，
故应填数值为：．
故答案为：．
（2）设关于的函数解析式为，得
．解得．
解析式为．
（3）如图所示：

（4）当背带的总长度为时，
可得
．
答：此时活动带末使用部分的长度为．
26．（12分）如图1，在长方形中，，有一只蚂蚁从点处开始以每秒1个单位的速度沿边向点爬行，另一只蚂蚁从点以每秒1个单位的速度沿边向点爬行，蚂蚁的大小忽略不计，如果同时出发，设运动时间为秒．
(1)当时，的面积是______；
(2)如图2，当是以为底的等腰三角形时，求的值；
(3)当同时运动3秒时，点停止运动，点立即以原速向点返回，在返回的过程中，是否存在点，使得平分？若存在，求出点运动的时间，若不存在，请说明理由．
答案：(1)4
(2)1.5
(3)存在，
（1）由题意可知，当时，，，
，
四边形是矩形，
，
，
故答案为：4；
（2）是以为底的等腰三角形
当是以为底的等腰三角形时，
（3）如图，过点作于点，连接
平分
，且，
点运动
，且
Rt
27．（12分）如图，在下列带有坐标系的网格中，△ABC的顶点都在边长为1的小正方形的顶点上，A（﹣3，3），B（﹣4，﹣2），C（0，﹣1）．
（1）直接写出△ABC的面积为 ；
（2）画出△ABC关于y轴的对称的△DEC（点D与点A对应，点E与点B对应），点E的坐标为 ；
（3）用无刻度的直尺，运用所学的知识作图（保留作图痕迹）．
①作出△ABC的高线AF
②在边BC上确定一点P，使得∠CAP＝45°．
答案：（1）；（2）（4，-2）；（3）①AF为△ABC的高作法见详解；②∠CAP=45°，作法见详解．
解：（1）S△ABC=S△ABH+S梯形AHGC-S△BCG
=
，
故答案为；
（2）∵A（﹣3，3），B（﹣4，﹣2），C（0，﹣1）．△ABC关于y轴的对称的△DEC，
∴点D（3，3），点E（4，-2），
描点D、E，连结CD，DE，EC，
则△DEC为△ABC关于y轴对称的三角形，
故答案为（4，-2）；
（3）①根据勾股定理AB=，过C向左5格向上1格作CH=，则CH⊥AB， 根据勾股定理AC=，过B向右4格，向上3格作BI，CH与BI交于G，则BI⊥AC，则点G为垂心，过A作射线AG交BC于F，则AF为所求，
AF为△ABC的高；
②根据AC=，过C先下3格，向左4格，作CR=，连结AR交BC于P，则RC⊥AC，RC=AC，
∴△ACR是等腰直角三角形，
∴∠RAC=∠ARC=45°，
则∠CAP=45°，
28．（12分）如图，在平面直角坐标系内，有一个等腰．
（1）如图1，点，点，点C的坐标为________．
（2）如图2，点，点B在y轴负半轴上，点C在第一象限，过点C作垂直于x轴于点H，则的值为___________．
（3）如图3，点B与原点重合，点A在x轴负半轴上，点C在y轴正半轴上，点D为x轴正半轴上一点，点M为线段中点，在y轴正半轴上取点E，使，过点D作，交的延长线于点F，请补全图形，判断与的数量关系，并证明你的结论．
答案：（1）C（1，3）；（2）4；（3）CD＝DF；证明见解析．
解：（1）如图1中，过点C作CR⊥y轴于R．
∵点A（−4，0），点B（0，−1），
∴OA＝4，OB＝1，
∵∠AOB＝∠ABC＝∠CHB＝90°，
∴∠ABO＋∠CBR＝90°，∠CBR＋∠BCR＝90°，
∴∠ABO＝∠BCR，
∵AB＝BC，
∴△AOB≌△BRC（AAS），
∴BR＝AO＝4，CR＝OB＝1，
∴OR＝BR−OB＝3，
∴C（1，3）．
故答案为：（1，3）．
（2）如图2中，过点C作CH⊥x轴于H，过点B作BT⊥CH交CH的延长线于T，设AH交BC于点J．
∵∠ABJ＝∠CHJ＝90°，∠AJB＝∠CJH，
∴∠BAO＝∠BCT，
∵∠AOB＝∠T＝90°，AB＝BC，
∴△AOB≌△CTB（AAS），
∴AO＝CT，
∵∠BOH＝∠OHT＝∠T＝90°，
∴四边形OHTB是矩形，
∴OB＝HT，
∴CH＋OB＝CH＋HT＝CT＝4．
故答案为：4．
（3）结论：CD＝DF．
理由：连接AE，延长AE交CD于J．
∵OA＝OC，∠AOE＝∠COD＝90°，CE＝OD，
∴△AOE≌△COD（SAS），
∴∠OAE＝∠OCD，AE＝CD，
∵∠CEJ＝∠AEO，
∴∠CJE＝∠AOE＝90°，
∴AJ⊥CD，
∵DF⊥CD，
∴AJ∥DF，
∴∠AEM＝∠DFM，
∵∠AME＝∠DMF，AM＝MD，
∴△AME≌△DMF（AAS），
∴AE＝DF，
∴CD＝DF．
活动带未使用部分的长度
5
10
15
20
30
背带的总长度
65
60
55
活动带未使用部分的长度
5
10
15
20
30
背带的总长度
65
60
55