2025年中考数学一轮复习讲练测课件第33讲 统计（含解析）

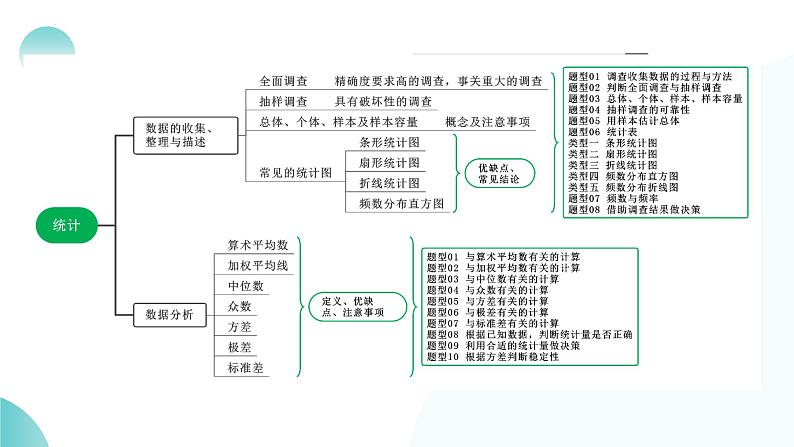
这是一份2025年中考数学一轮复习讲练测课件第33讲 统计（含解析），共38页。PPT课件主要包含了知识建构，考点精讲，考情分析，第一部分，第二部分，第三部分等内容，欢迎下载使用。

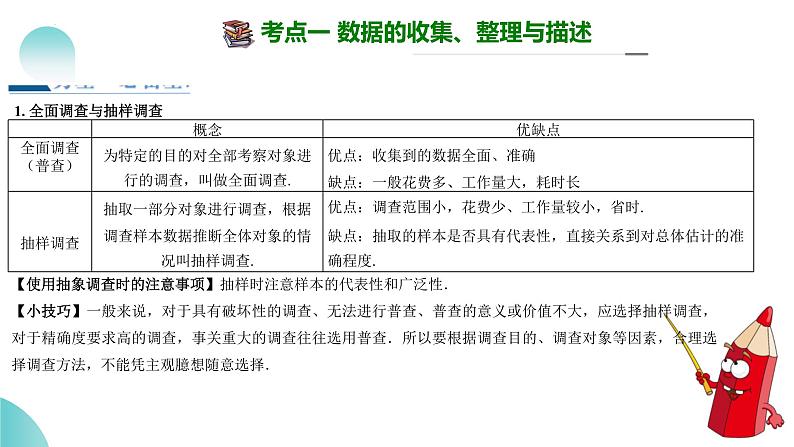
1. 全面调查与抽样调查
【使用抽象调查时的注意事项】抽样时注意样本的代表性和广泛性．【小技巧】一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．所以要根据调查目的、调查对象等因素，合理选择调查方法，不能凭主观臆想随意选择．
2. 总体、个体、样本及样本容量
3. 几种常见的统计图
1. 条形统计图中每个小长方形的高即为该组对象数据的个数（频数），各小长方形的高之比等于相应的个数（频数）之比.2. 扇形统计图中，用圆代表总体，扇形的大小代表各部分数量占总体数量的百分数，但是没有给出具体数值，因此不能通过两个扇形统计图来比较两个统计量的多少.3. 在利用折线统计图比较两个统计量的变化趋势时，要保证两个图中横、纵坐标的一致性，即坐标轴上同一单位长度所表示的意义应该一致.4. 画频数分布直方图时，分组要遵循三个原则：不空，即该组必须有数据；不重，即一个数据只能在一个组；不漏，即不能漏掉某一个数据.
题型01 调查收集数据的过程与方法
题型02 判断全面调查与抽样调查
【例2】（2023·浙江嘉兴·统考一模）下列调查中，适宜采用全面调查方式的是（    ）A．检测“神舟十四号”载人飞船零件的质量B．检测一批LED灯的使用寿命C．检测黄冈、孝感、咸宁三市的空气质量D．检测一批家用汽车的抗撞击能力【变式2-1】（2022·贵州贵阳·统考模拟预测）下列调查中，适宜采用抽样调查的是（    ）A．调查某班学生的身高情况B．调查亚运会100m游泳决赛运动员兴奋剂的使用情况C．调查某批汽车的抗撞击能力D．调查一架“歼10”隐形战斗机各零部件的质量
题型03 总体、个体、样本、样本容量
【例3】（2022·贵州贵阳·统考模拟预测）某校有4000名学生，随机抽取了400名学生进行体重调查，下列说法错误的是（    ）A．总体是该校4000名学生的体重B．个体是每一个学生C．样本是抽取的400名学生的体重D．样本容量是400【变式3-1】（2023·江苏无锡·统考二模）为了调查我市某校学生的视力情况，在全校的2000名学生中随机抽取了300名学生，下列说法正确的是（    ）A．此次调查属于全面调查B．样本容量是300C．2000名学生是总体D．被抽取的每一名学生称为个体
题型04 抽样调查的可靠性
【例4】（2022·河南南阳·统考一模）为了解游客在开封、洛阳和安阳这三个城市旅游的满意度，数学小组的同学商议了几个收集数据的方案．方案一：在多家旅游公司调查1000名导游；方案二：在洛阳调查1000名游客；方案三：在开封调查1000名游客；方案四：在三个城市各调查1000名游客．其中最合理的是（    ）．A．方案一B．方案二C．方案三D．方案四【变式4-1】（2020·浙江杭州·模拟预测）抽样调查放学时段，学校附近某路口车流量情况的样本中，下列最合适的是（　　　）A．抽取一月份第一周为样本B．抽取任意一天为样本C．选取每周日为样本 D．每个季节各选两周作为样本
题型05 用样本估计总体
【例5】（2023·河北·模拟预测）嘉淇调查了本班学生最喜欢的体育项目情况，并绘制成如图所示的扇形统计图和条形统计图，其中条形统计图被撕坏了一部分，则m与n的和为（    ）A．24B．26C．52D．54
题型06 统计表 类型一 条形统计图
【例6】（2021·湖南长沙·长沙市开福区青竹湖湘一外国语学校校考二模）某校饭堂随机抽取了100名学生，对他们最喜欢的套餐种类进行问卷调查后（每人选一种），绘制了如图的条形统计图，根据图中的信息，学生最喜欢的套餐种类是（  ）A．套餐一B．套餐二C．套餐三D．套餐四
【例8】（2023·湖南株洲·模拟预测）射击比赛中，某队员的10次射击成绩如图所示，则下列结论错误的是（    ）A．平均数是9环B．中位数是9环C．众数是9环D．方差是0.8
【例9】（2023·湖南湘西·统考一模）今年是中国共产主义青年团成立100周年，某校组织学生观看庆祝大会实况并进行团史学习．现随机抽取部分学生进行团史知识竞赛，并将竞赛成绩（满分100分）进行整理（成绩得分用a表示），其中60≤a<70记为“较差”，70≤a<80记为“一般”，80≤a<90记为“良好”，90≤a≤100记为“优秀”，绘制了不完整的扇形统计图和频数分布直方图．请根据统计图提供的信息，回答如下问题：(1)x=________，y=________，并将直方图补充完整；(2)已知90≤a≤100这组的具体成绩为93，94，99，91，100，94，96，98，则这8个数据的中位数是________，众数是________；(3)若该校共有1200人，估计该校学生对团史掌握程度达到优秀的人数；(4)本次知识竞赛超过95分的学生中有3名女生，1名男生，现从以上4人中随机抽取2人去参加全市的团史知识竞赛，请用列表或画树状图的方法，求恰好抽中2名女生参加知识竞赛的概率．
类型四 频数分布直方图
类型五 频数分布折线图
题型08 借助调查结果做决策
【例12】（2022·河南洛阳·统考二模）短视频因其交互性强、地域不受限制、受众可划分等特点而广受欢迎，但也不可避免传播了低俗扭曲的不良信息．某市网监办设计了对短视频的态度问卷，四种态度：非常支持、坚决取缔、无所谓、引导管控（以下分别用A，B，C，D表示），调查者在社区对各年龄段居民进行了随机抽查，并将调查结果绘制成两幅不完整的统计图．请根据以上信息解答：(1)本次参加抽样调查的居民有_____________人；(2)将条形统计图补充完整，并计算扇形统图中A所对圆心角的度数为_____________．(3)请根据统计情况，对短视频的去留提出合理化建议．
题型01 与算术平均数有关的计算
【例1】（2022·江苏·统考模拟预测）已知两组数据x，x2，…，xn和y1，y2，…，yn的平均数分别为2和－2，则x1＋3y1，x2＋3y2，…，xn＋3yn的平均数为（    ）A．－4B．－2C．0D．2
题型02 与加权平均数有关的计算
【例2】（2022·河南郑州·统考一模）小明参加校园歌手比赛，唱功得85分，音乐常识得95分，综合知识得90分，学校如果按如图所示的权重计算总评成绩，那么小明的总评成绩是（    ）A．87分B．87.5分C．88.5分D．89分
题型03 与中位数有关的计算
【例3】（2022·江苏南京·统考二模）已知一组数据1，2，3，4，5，a，b的平均数是4，若该组数据的中位数小于4，则a的值可能是（    ）A．7B．8C．9D．10
题型04 与众数有关的计算
【例4】（2023·新疆·统考一模）如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况（满分5分），则所打分数的众数为（    ）A．5分B．4分C．3分D．45%
【详解】解：由扇形统计图可知：1分所占百分比：5%；2分所占百分比：10%；3分所占百分比：25%；4分所占百分比：45%；5分所占百分比：15%；可知，4分所占百分比最大，故4分出现的次数最多，∴所打分数的众数为4；故选：B．
题型05 与方差有关的计算
题型6 根据方差判断稳定性
题型07 与极差有关的计算
题型08 与标准差有关的计算
题型09 根据已知数据，判断统计量是否正确
【例9】（2023·山东泰安·校考模拟预测）五名同学捐款数分别是5，3，6，5，10（单位：元），捐10元的同学后来又追加了10元．追加后的5个数据与之前的5个数据相比，集中趋势相同的是（    ）A．只有平均数B．只有中位数C．只有众数D．中位数和众数
题型10 利用合适的统计量做决策