



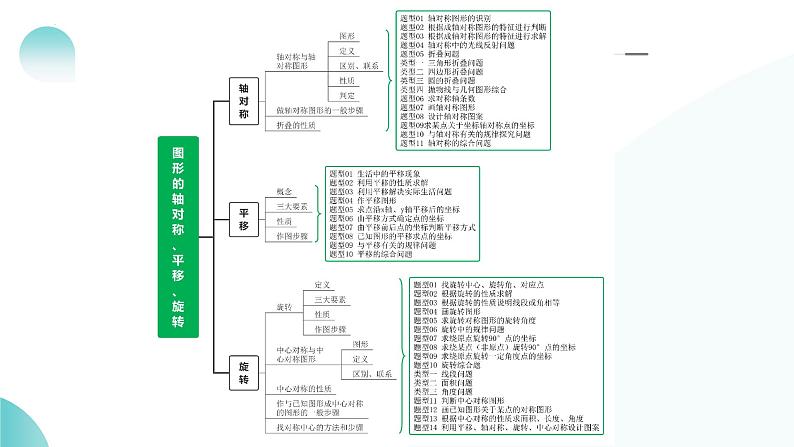

所属成套资源:2025年中考数学一轮复习讲练测课件 (含解析)
2025年中考数学一轮复习讲练测课件第31讲 轴对称、平移、旋转(含解析)
展开这是一份2025年中考数学一轮复习讲练测课件第31讲 轴对称、平移、旋转(含解析),共60页。PPT课件主要包含了知识建构,考点精讲,考情分析,第一部分,第二部分,第三部分等内容,欢迎下载使用。
常见的轴对称图形有:圆、正方形、长方形、菱形、等腰梯形、等腰三角形、等边三角形等.做轴对称图形的一般步骤:1)作某点关于某直线的对称点的一般步骤:①过已知点作已知直线(对称轴)的垂线,标出垂足,并延长;②在延长线上从垂足出发截取与已知点到垂足的距离相等的线段,那么截点就是这点关于该直线的对称点.2)作已知图形关于某直线的对称图形的一般步骤:①找.在原图形上找特殊点(如线段的端点、线与线的交点)②作.作各个特殊点关于已知直线的对称点③连.按原图对应连接各对称点折叠的性质:折叠的实质是轴对称,折叠前后的两图形全等,对应边和对应角相等.【解题思路】凡是在几何图形中出现“折叠”这个字眼时,第一反应即存在一组全等图形,其次找出与要求几何量相关的条件量.解决折叠问题时,首先清楚折叠和轴对称能够提供我们隐含的且可利用的条件,分析角之间、线段之间的关系,借助勾股定理建立关系式求出答案,所求问题具有不确定性时,常常采用分类讨论的数学思想方法.
1. 对称轴是一条直线,不是一条射线,也不是一条线段.2. 轴对称图形的对称轴有的只有一条,有的存在多条对称轴(例:正方形有四条对称轴,圆有无数条对称轴等).3. 成轴对称的两个图形中的任何一个都可以看作由另一个图形经过轴对称变换得到的,一个轴对称图形也可以看作以它的一部分为基础,经轴对称变换得到的.4. 轴对称的性质是证明线段相等、线段垂直及角相等的依据之一,例如:若已知两个图形关于某直线成轴对称,则它们的对应边相等,对应角相等.
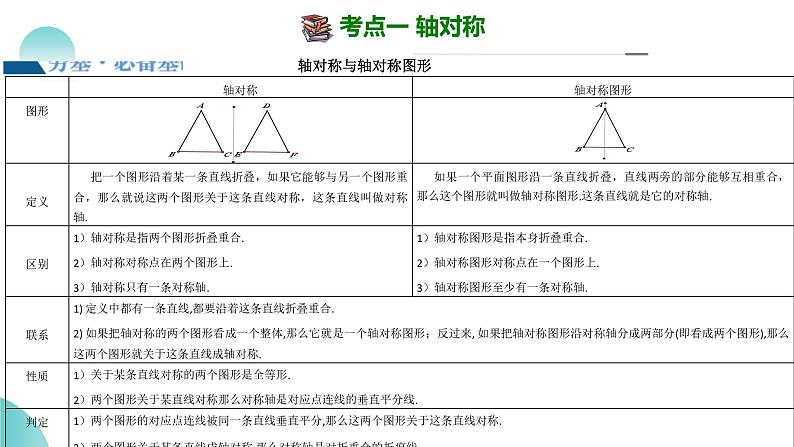
题型01 轴对称图形的识别
题型02 根据成轴对称图形的特征进行判断
题型03 根据成轴对称图形的特征进行求解
题型04 轴对称中的光线反射问题
题型05 折叠问题 类型一 三角形折叠问题
题型05 折叠问题 类型二 四边形折叠问题
题型05 折叠问题 类型三 圆的折叠问题
题型05 折叠问题 类型四 抛物线与几何图形综合
题型06 求对称轴条数
题型07 画轴对称图形
题型08 设计轴对称图案
【例11】(2020·山东枣庄·统考二模)在数学活动课上,王老师要求学生将图1所示的3×3正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分) 请在图中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂黑(每个3×3的正方形方格画一种,例图除外)
题型09求某点关于坐标轴对称点的坐标
题型10 与轴对称有关的规律探究问题
【例13】(2022·云南·云大附中校考一模)如图,在平面直角坐标系中,四边形ABCD是平行四边形,A(﹣1,3)、B(1,1)、C(5,1).规定“把▱ABCD先沿y轴翻折,再向下平移1个单位”为一次变换.如此这样,连续经过2022次变换后,▱ABCD的顶点D的坐标变为( )A.(3,﹣2019)B.(﹣3,﹣2019)C.(3,﹣2018)D.(﹣3,﹣2018)
【详解】解:∵四边形ABCD是平行四边形,A(﹣1,3)、B(1,1)、C(5,1),∴D(3,3),∵把▱ABCD先沿y轴翻折,再向下平移1个单位为一次变换,又∵沿y轴翻折横坐标为相反数,纵坐标不变,∴第一次变换后,D(-3,2),第二次变换后,D(3,1),……∴对于横坐标,奇数次变换为-3,偶数次变换为3,对于纵坐标,每次变换减一,∴经过2022次变换后,D(3,﹣2019).故选:A.
题型11 轴对称的综合问题
【详解】解:如图,连接EC,GC,设EC交AF于点G′,连接DG′.∵正五边形ABCDE中,点F是DC的中点,AF⊥DC,∴D,C关于AF对称,∴GD=GC,∵EG+GD=EG+GC≥EC,∴当点G与G′重合时,EG+DG的值最小,△DEG的周长最小,∵ABCDE是正五边形,∴ED=DC,∠EDC=108°,∴∠DEC=∠DCE=36°,∵G′D=G′C,∴∠G′DC=∠DCG′=36°,∴∠D G′C=108°,∴∠EG′D=180°-∠DG′C=180°-108°=72°.故选:C.
平移的概念:在平面内,一个图形由一个位置沿某个方向移动到另一个位置,这样的图形运动叫做平移.平移不改变图形的形状和大小.平移的三大要素:1)平移的起点,2)平移的方向,3)平移的距离.平移的性质:1)平移不改变图形的大小、形状,只改变图形的位置,因此平移前后的两个图形全等.2)平移前后对应线段平行且相等、对应角相等.3)任意两组对应点的连线平行(或在同一条直线上)且相等,对应点之间的距离就是平移的距离.作图步骤:1)根据题意,确定平移的方向和平移的距离;2)找出原图形的关键点;3)按平移方向和平移距离平移各个关键点,得到各关键点的对应点;4)按原图形依次连接对应点,得到平移后的图形.
题型01 生活中的平移现象
【例1】(2022·贵州贵阳·统考二模)下列现象中属于平移的是( )①方向盘的转动;②打气筒打气时,活塞的运动;③钟摆的摆动;④汽车雨刷的运动A.①②B.②③C.①②④D.②
题型02 利用平移的性质求解
题型03 利用平移解决实际生活问题
【例3】(2023·山东淄博·统考二模)如图,在长为37米,宽为26米的长方形地块上,有纵横交错的几条小路,宽均为1米,其它部分均种植花草,则种植花草的面积 平方米.
题型05 求点沿x轴、y轴平移后的坐标
题型06 由平移方式确定点的坐标
【例6】(2021·江西·统考一模)如图,P(m,n)为△ABC内一点,△ABC经过平移得到△A′B′C′,平移后点P与其对应点P'关于x轴对称,若点B的坐标为(﹣2,1),则点B的对应点B′的坐标为( )A.(﹣2,1﹣2n)B.(﹣2,1﹣n)C.(﹣2,﹣1)D.(m,﹣1)
题型07 由平移前后点的坐标判断平移方式
【例7】(2022·山东淄博·统考二模)四盏灯笼的位置如图.已知A,B,C,D的坐标分别是 (−1,b),(1,b),(2,b),(3.5,b),平移y轴右侧的一盏灯笼,使得y轴两侧的灯笼对称,则平移的方法可以是( )A.将B向左平移4.5个单位B.将C向左平移4个单位C.将D向左平移5.5个单位D.将C向左平移3.5个单位
题型08 已知图形的平移求点的坐标
【例8】(2023·辽宁大连·模拟预测)如图,在平面直角坐标系中,平移△ABC至△A1B1C1的位置.若顶点A(﹣3,4)的对应点是A1(2,5),则点B(﹣4,2)的对应点B1的坐标是 .
题型09 与平移有关的规律问题
题型10 平移的综合问题
定义:在平面内,一个图形绕一个定点沿某个方向(顺时针或逆时针)转过一个角度,这样的图形运动叫旋转.这个定点叫做旋转中心,转过的这个角叫做旋转角.三大要素:旋转中心、旋转方向和旋转角度.性质:1)对应点到旋转中心的距离相等;2)每对对应点与旋转中心所连线段的夹角等于旋转角;3)旋转前后的图形全等.作图步骤:1)根据题意,确定旋转中心、旋转方向及旋转角;2)找出原图形的关键点;3)连接关键点与旋转中心,按旋转方向与旋转角将它们旋转,得到各关键点的对应点;4)按原图形依次连接对应点,得到旋转后的图形.
1. 图形的旋转由旋转中心、旋转方向与旋转的角度所决定.2. 旋转中心可以是图形外的一点,也可以是图形上的一点,还可以是图形内的一点.3. 对应点之间的运动轨迹是一段圆弧,对应点到旋转中心的线段就是这段圆弧所在圆的半径.4. 旋转是一种全等变换,旋转改变的是图形的位置,图形的大小关系不发生改变,所以在解答有关旋转的问题时,要注意挖掘相等线段、角,因此特殊三角形性质的运用、锐角三角函数建立的边角关系起着关键的作用.
中心对称与中心对称图形:
中心对称的性质:1)中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;中心对称的两个图形是全等图形.
作与已知图形成中心对称的图形的一般步骤:1)作已知图形各顶点(或决定图形形状的关键点)关于对称中心的对称点——连接关键点和对称中心,并延长一倍确定关键点的对称点.2)把各对称点按已知图形的连接方式依次连接起来,则所得到的图形就是已知图形关于对称中心对称的图形.找对称中心的方法和步骤:方法1:连接两个对应点,取对应点连线的中点,则中点为对称中心.方法2:连接两个对应点,在连接两个对应点,两组对应点连线的交点为对称中心.
【例1】(2019·山东·山东省青岛第二十六中学校考中考模拟)如图,在平面直角坐标系中,△ABC的顶点都在方格线的格点上,将三角形ABC绕点P旋转90°,得到△A′B′C′,则点P的坐标为( )A.(0,4)B.(1,1)C.(1,2)D.(2,1)【变式1-1】(2022·四川泸州·统考一模)如图,△ABC绕点C旋转,点B转到点E的位置,则下列说法正确的是( )A.点B与点D是对应点B.∠BCD等于旋转角C.点A与点E是对应点D.△ABC≌△DEC
题型01 找旋转中心、旋转角、对应点
题型02 根据旋转的性质求解
题型03 根据旋转的性质说明线段或角相等
题型05 求旋转对称图形的旋转角度
题型06 旋转中的规律问题
【详解】解:根据题意可得:小正方形沿着矩形ABCD的边AB→BC→CD→DA→AB连续地翻转,矩形ABCD的边长AB和BC分别是3cm和2cm,小正方形的边长为1cm,则这个小正方形第一次回到起始位置时需10次翻转,而每翻转4次,它的方向重复1次,故回到起始位置时它的方向是向下.故选:C.
题型07 求绕原点旋转90°点的坐标
题型08 求绕某点(非原点)旋转90°点的坐标
题型09 求绕原点旋转一定角度点的坐标
题型10 旋转综合题 类型一 线段问题
【例10】(2023·陕西·模拟预测)如图,在正方形ABCD中,AB=4,G是BC的中点,点E是正方形内一个动点,且EG=2,连接DE,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,则线段CF长的最小值为 .
题型10 旋转综合题 类型二 面积问题
题型10 旋转综合题 类型三 角度问题
题型11 判断中心对称图形
题型12 画已知图形关于某点的对称图形
【例14】(2022·安徽安庆·校考一模)如图,在由边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).(1)画出△ABC关于点C成中心对称的△A'B'C(其中A'是点A的对应点,B'是点B的对应点);(2)用无刻度的直尺作出一个格点O,使得OA=OB.
题型13 根据中心对称的性质求面积、长度、角度
题型14 利用平移、轴对称、旋转、中心对称设计图案
相关课件
这是一份中考数学一轮复习 课件 第17讲 轴对称、平移、旋转,共27页。PPT课件主要包含了思维导图,夯实基础,考点1图形的轴对称,-1-2,考点2图形的旋转,ACCEEA,∠ACE,60°,直角三角形,全等形等内容,欢迎下载使用。
这是一份中考数学一轮复习考点讲练课件 :第24讲 图形的平移、旋转和对称,共48页。PPT课件主要包含了旋转角,中心对称,全等图形,对称中心,轴对称常考点,对称轴,垂直平分,垂直平分线,图形的平移,图形a等内容,欢迎下载使用。
这是一份第31讲 轴对称、平移、旋转(课件)-2024年中考数学一轮复习课件(全国通用),共60页。PPT课件主要包含了考情分析,知识建构,考点精讲等内容,欢迎下载使用。












