人教A版 (2019)1.3 空间向量及其运算的坐标表示精品同步练习题

这是一份人教A版 (2019)1.3 空间向量及其运算的坐标表示精品同步练习题，文件包含人教版高中数学选择性必修一精讲精练13空间向量及其运算的坐标表示精讲原卷版docx、人教版高中数学选择性必修一精讲精练13空间向量及其运算的坐标表示精讲解析版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。


考点一 空间向量的坐标表示
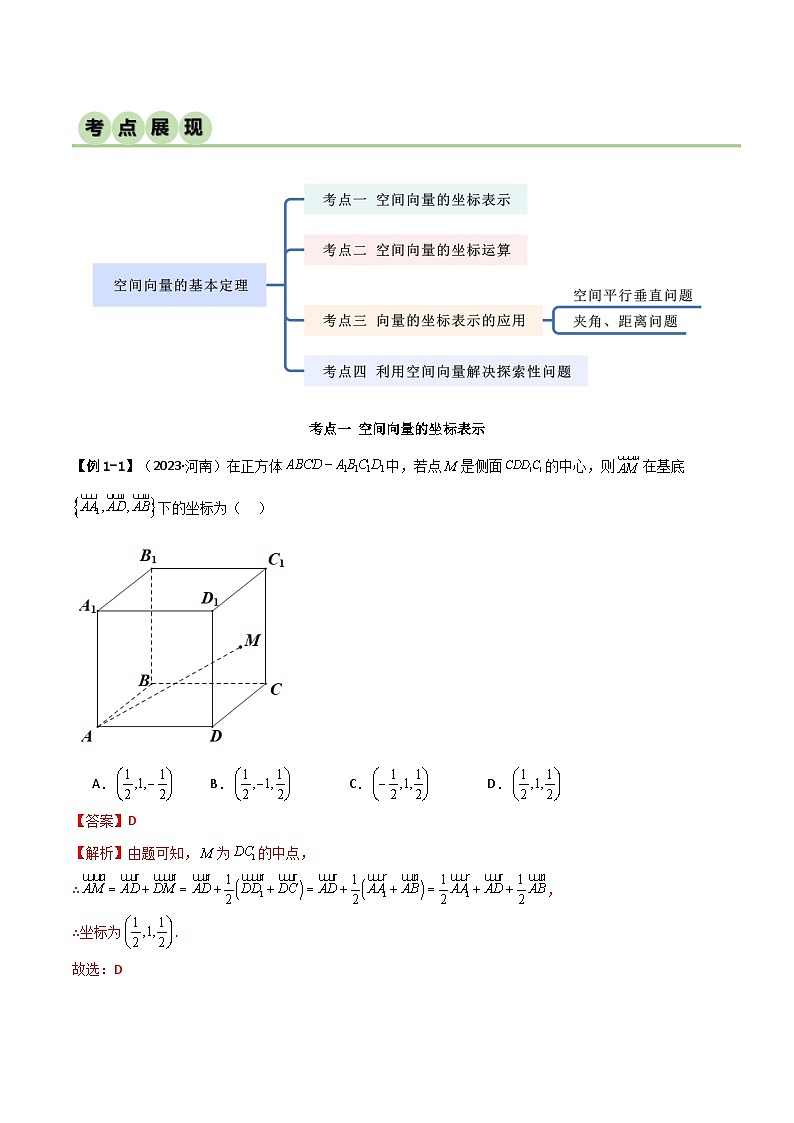
【例1-1】（2023·河南）在正方体中，若点是侧面的中心，则在基底下的坐标为（ ）
A．B．C．D．
【答案】D
【解析】由题可知，为的中点，
∴，
∴坐标为.
故选：D
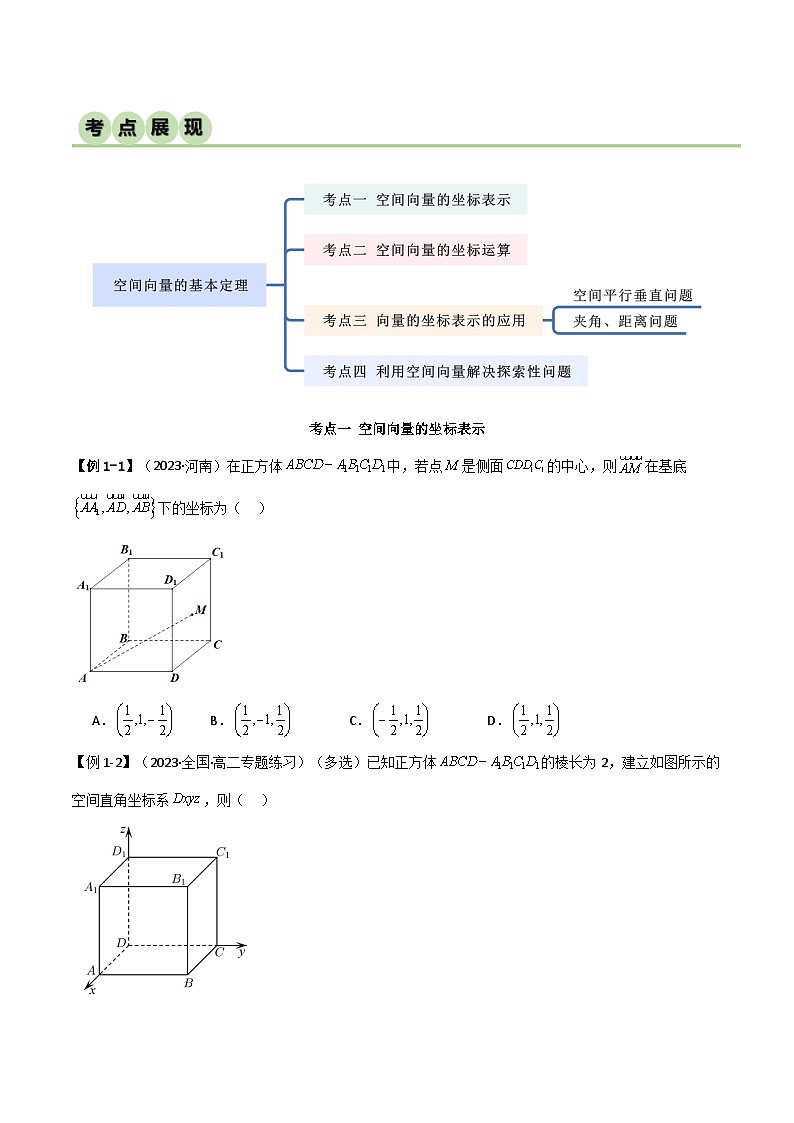
【例1-2】（2023·全国·高二专题练习）（多选）已知正方体的棱长为2，建立如图所示的空间直角坐标系，则（ ）
A．点的坐标为（2，0，2）B．
C．的中点坐标为（1，1，1）D．点关于y轴的对称点为（－2，2，－2）
【答案】BCD
【解析】根据题意可知点的坐标为，故A错误；
由空间直角坐标系可知： ,故B正确；
由空间直角坐标系可知：,故的中点坐标为（1，1，1），故C正确；
点坐标为，关于于y轴的对称点为（－2，2，－2），故D正确，
故选：BCD
【例1-3】．（2023春·高二课时练习）如图，在直三棱柱ABC­A1B1C1的底面△ABC中，CA＝CB＝1，∠BCA＝90°，棱AA1＝2，M，N分别为A1B1，A1A的中点，试建立恰当的坐标系求向量，，的坐标．
【答案】＝(1，－1，1)，＝(1，－1，2)，＝(－1，1，－2)．
【解析】由题意知CC1⊥AC，CC1⊥BC，AC⊥BC，以点C为原点，分别以CA，CB，CC1的方向为x轴，y轴，z轴的正方向建立空间直角坐标系C­xyz，如图所示．
则B(0，1，0)，A(1，0，0)，A1(1，0，2)，N(1，0，1)，
∴＝(1，－1，1)，＝(1，－1，2)，＝(－1，1，－2)．
【一隅三反】
1．（2023·北京）（多选）如图，在正三棱柱中，已知的边长为2，三棱柱的高为的中点分别为，以为原点，分别以的方向为轴､轴､轴的正方向建立空间直角坐标系，则下列空间点及向量坐标表示正确的是（ ）
A．B．
C．D．
【答案】ABC
【解析】在等边中，，所以，则，，则.
故选：ABC
2．（2023山东）如图，在长方体ABCD-A1B1C1D1中，E，F分别为D1C1，B1C1的中点，若以为基底，则向量的坐标为___，向量的坐标为___，向量的坐标为___.
【答案】
【解析】因为，所以向量的坐标为.
因为，
所以向量的坐标为.
因为，所以向量的坐标为.
故答案为：；；
3．（2023春·高二课时练习）在平行六面体中，底面是矩形，，，平行六面体高为，顶点在底面的射影是中点，设的重心，建立适当空间直角坐标系并写出下列点的坐标.

(1)；
(2)；
(3)；
【答案】(1)，，，
(2)
(3)
【解析】1）
如图，以为坐标原点，分别以所在直线为轴，以过点作的平行线为轴建立空间直角坐标系．
设点，点在平面上则，
由图可知它到轴投影对应数值，则，
到轴投影对应数值为，则，即，
设点，点在平面上则，
由图可知它到轴投影对应数值，则，
到轴投影对应数值为，则，即，
设点，点在平面上则，
由图可知它到轴投影对应数值，则，
到轴投影对应数值为，则，即，
且点在轴上，则.
（2）是的重心，由三角形重心公式可得
.
（3）设，且，则，，
又 ，即
点B坐标为.
考点二 空间向量的坐标运算
【例2-1】（2023湖北）（多选）已知向量，，则下列结论正确的是（ ）
A．B．
C．D．
【答案】ACD
【解析】因为，，
所以，，，
.故正确的选项为ACD.
故选：ACD
【例2-2】（2022·四川省蒲江县蒲江中学）设、，向量，，且，，则（ ）
A．B．C．D．
【答案】D
【解析】因为，则，解得，则，
因为，则，解得，即，
所以，，因此，.故选：D.
【一隅三反】
1．（2023陕西）（多选）已知向量，则下列结论正确的是（ ）
A．
B．
C．
D．
【答案】AD
【解析】因为，
所以，故A正确；
，故B错误；
，故C错误；
，故D正确.
故选：AD.
2．（2022·福建省）（多选）已知空间向量，，则下列结论正确的是（ ）
A． B． C． D．与夹角的余弦值为
【答案】BCD
【解析】对于A选项：，不存在，使得，故A错误；
对于B选项：，，故B正确；
对于C选项：，，
则，故C正确；对于D选项：，，
所以，故D正确；故选：BCD.
3．（2023·江苏·高二专题练习）（1）已知向量.
①计算和
②求.
（2）已知向量.
①若，求实数；
②若，求实数.
【答案】（1）①，；②；（2）①；②
【解析】（1）①向量，
，，
②，即
，，
（2）因为向量，
，
①，
，解得，
②，
，解得.
考点三 向量的坐标表示的应用
【例3-1】（2023上海）如图，已知直三棱柱ABC－A1B1C1，在底面△ABC中，CA＝CB＝1，∠BCA＝90°，棱AA1＝2，M，N分别是A1B1，A1A的中点．
（1）求 的模；
（2）求cs〈，〉的值；
（3）求证：A1B⊥C1M.
【答案】（1）；（2）；（3）证明见解析.
【解析】（1）如图，以点C作为坐标原点O，CA，CB，CC1所在直线分别为x轴，y轴，z轴，建立空间直角坐标系. 由题意得B(0，1，0)，N(1，0，1)，
∴＝＝.
（2）由题意得A1(1，0，2)，B(0，1，0)，C(0，0，0)，B1(0，1，2)，
∴＝(1，－1，2)，＝(0，1，2)，
·＝3，||＝，||＝，
∴cs〈，〉＝＝.
（3）由题意得C1(0，0，2)，M，＝(－1，1，－2)，＝，
∴·＝－＋＋0＝0，
∴⊥，即A1B⊥C1M.
【一隅三反】
1．（2023·广东佛山·高二校考阶段练习）如图所示，在直三棱柱中，，，棱，、分别为、的中点.建立适当的空间直角坐标系，解决如下问题：
(1)求的模；
(2)求的值；
(3)求证：平面.
【答案】(1)
(2)
(3)证明见解析
【解析】（1）解：因为平面，，
以点为坐标原点，、、所在直线分别为、、轴建立如下图所示的空间直角坐标系，
则，，所以，，则.
（2）解：依题意得、、、，
所以，，，，
又，，
所以，.
（3）证明：依题意得、、、、，
则，，，
所以，，，
则，，即，，
又因为，所以，平面.
2．（2023广西）已知长方体中,，点N是AB的中点，点M是的中点．建立如图所示的空间直角坐标系．
（1）写出点的坐标；
（2）求线段的长度；
（3）判断直线与直线是否互相垂直，说明理由．
【答案】（1）；（2）；（3）不垂直，理由见解析.
【解析】（1）由于为坐标原点，所以
由得：
点N是AB的中点，点M是的中点，；
（2）由两点距离公式得：，
；
（3）直线与直线不垂直
理由：由（1）中各点坐标得：
与不垂直，所以直线与直线不垂直
3．（2023天津）如图，在四棱锥中，底面为正方形，侧棱底面，，，分别为，，的中点．若，．
(1)求；
(2)求．
【答案】(1)
(2)
【解析】（1）以为原点，分别以射线､､为轴､轴､轴的正半轴，建立空间直角坐标系.
则，，，，，，
所以，则.

（2）由（1）知，，
所以；
考点四 空间向量解决探索问题
【例4】（2022·高二课时练习）在直三棱柱中，，，，．
(1)在上是否存在点，使得？
(2)在上是否存在点，使得平面？
【答案】(1)存在
(2)存在
【解析】(1)直三棱柱中，，，，则、、 两两垂直
如图，以为坐标原点，射线、、分别为轴的正向建立空间直角坐标系，则，，，，．
（1）假设在AB上存在点D，使得，
则，其中，则，于是，
由于，且，所以，得，
所以在AB上存在点D，使得，且这时点D与点B重合．
(2)
假设在AB上存在点D，使得平面，则，其中，
则，．
又，，平面，
所以存在实数，使成立，
∴，，．
所以，所以在上存在点使得平面，且是的中点．
【一隅三反】
1．（2023·安徽滁州）已知．
(1)求；
(2)已知点在直线上，求的值；
(3)当为何值时，与垂直？
【答案】(1)
(2)
(3)
【解析】（1），
，
．
（2）因为点在直线上，与共线，
则存在使得，即，
，解得；
（3），
与垂直,
，
，
时，与垂直．
2．（2023·江苏·高二专题练习）在①，②，③这三个条件中任选一个，补充在下面的问题中，并作答．
问题：如图，在正方体，中，以为坐标原点，建立空间直角坐标系．已知点的坐标为，为棱上的动点，为棱上的动点，______，则是否存在点，，使得？若存在，求出的值；若不存在，请说明理由．
【答案】答案见解析
【解析】方案一：选条件①．
假设存在满足题意的点，．由题意，知正方体的棱长为2，则，，，，，所以．设，，则，，，所以，．
因为，所以，即．
因为，，所以，所以．又，
所以，故存在点，，满足，此时．
方案二：选条件②．
假设存在满足题意的点，．由题意，知正方体的棱长为2，则，，，，，所以．
设，，则，，，
所以，．因为，且，
所以，解得．又，所以，
故存在点，，满足，此时．
方案三：选条件③．假设存在满足题意的点，．由题意，知正方体的棱长为2，
则，，，，所以，．
设，，则．因为，
所以与不共线，所以，即，
则，
故不存在点，满足．