新高考数学考前考点冲刺精练卷12《函数的图象》（2份，原卷版+教师版）

这是一份新高考数学考前考点冲刺精练卷12《函数的图象》（2份，原卷版+教师版），文件包含新高考数学考前考点冲刺精练卷12《函数的图象》教师版pdf、新高考数学考前考点冲刺精练卷12《函数的图象》教师版doc、新高考数学考前考点冲刺精练卷12《函数的图象》原卷版doc、新高考数学考前考点冲刺精练卷12《函数的图象》原卷版pdf等4份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。

一、选择题
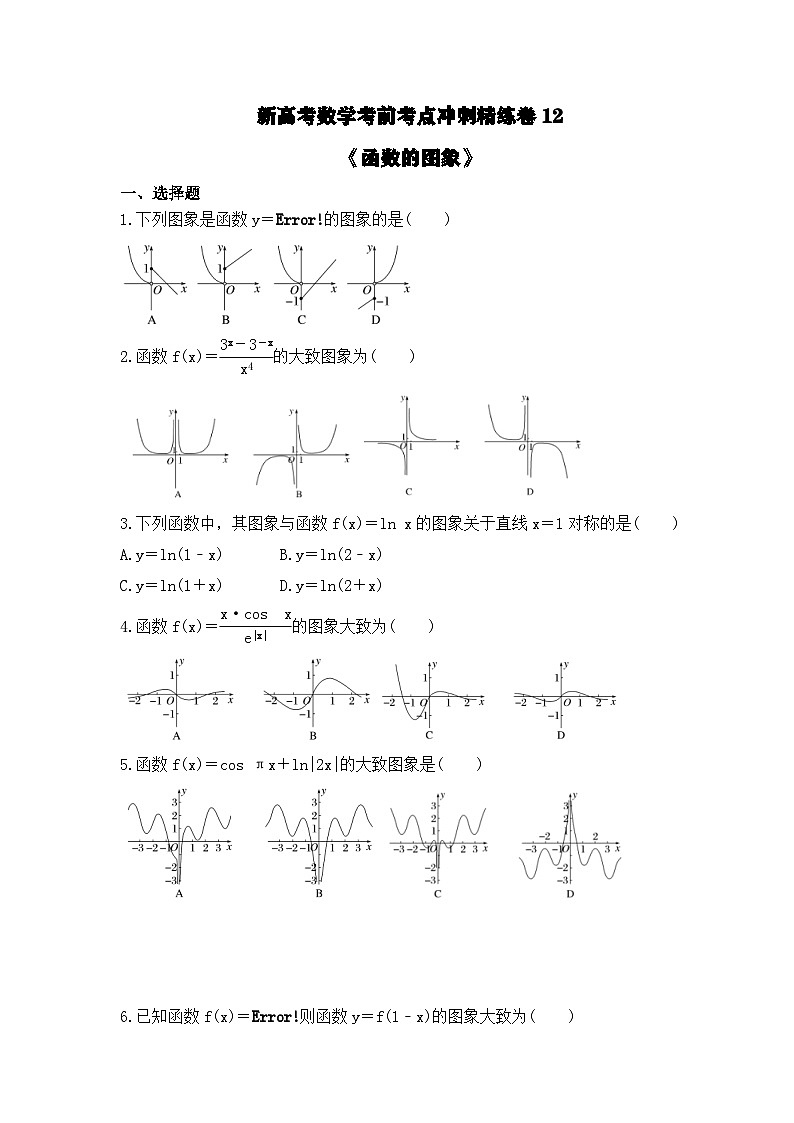
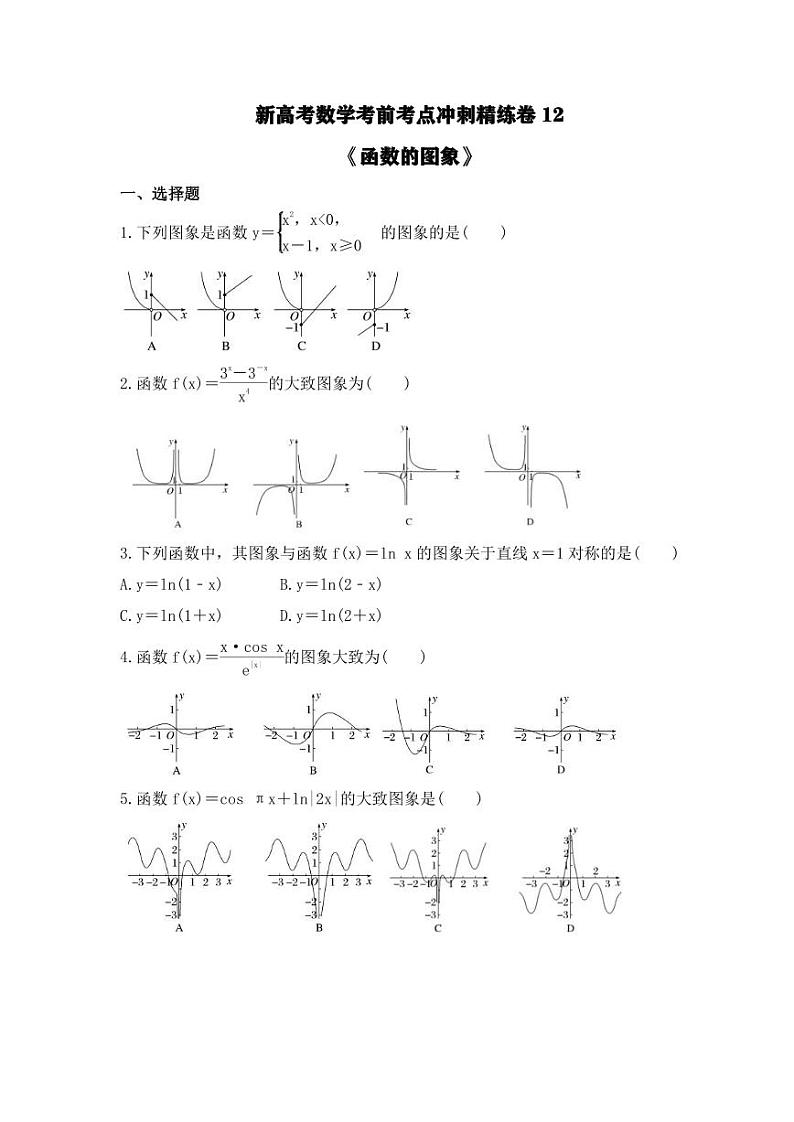
下列图象是函数y＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x2，x<0，,x－1，x≥0))的图象的是( )
【答案解析】答案为：C
解析：其图象是由y＝x2图象中x＜0的部分和y＝x﹣1图象中x≥0的部分组成.
函数f(x)＝eq \f(3x－3－x,x4)的大致图象为( )

【答案解析】答案为：B
解析：易知定义域为(﹣∞，0)∪(0，＋∞)，关于原点对称.f(﹣x)＝eq \f(3－x－3x,－x4)＝﹣eq \f(3x－3－x,x4)＝﹣f(x)，则f(x)是奇函数，其图象关于原点对称，排除A，f(1)＝3﹣eq \f(1,3)＝eq \f(8,3)＞0，排除D，当x→＋∞时，3x→＋∞，则f(x)→＋∞，排除C，选项B符合.
下列函数中，其图象与函数f(x)＝ln x的图象关于直线x＝1对称的是( )
A.y＝ln(1﹣x) B.y＝ln(2﹣x)
C.y＝ln(1＋x) D.y＝ln(2＋x)
【答案解析】答案为：B
解析：方法一 设所求函数图象上任一点的坐标为(x，y)，则其关于直线x＝1的对称点的坐标为(2﹣x，y)，由对称性知点(2﹣x，y)在函数f(x)＝ln x的图象上，所以y＝ln(2﹣x).
方法二 由题意知，对称轴上的点(1,0)既在函数f(x)＝ln x的图象上也在所求函数的图象上，代入选项中的函数解析式逐一检验，排除A，C，D.
函数f(x)＝eq \f(x·cs x,e|x|)的图象大致为( )
【答案解析】答案为：D
解析：由题意知，f(x)的定义域为R，f(﹣x)＝eq \f(－x·cs－x,e|－x|)＝eq \f(－x·cs x,e|x|)＝﹣f(x)，故f(x)为奇函数，排除C；f(1)＝eq \f(cs 1,e)＞0，排除A；f(2)＝eq \f(2cs 2,e2)＜0，排除B.
函数f(x)＝cs πx＋ln|2x|的大致图象是( )
【答案解析】答案为：C
解析：因为f(x)＝cs πx＋ln|2x|(x≠0)，所以f(﹣x)＝cs(﹣πx)＋ln|﹣2x|＝cs πx＋ln|2x|＝f(x)，所以f(x)是偶函数，其图象关于y轴对称，故排除选项A；
f(1)＝cs π＋ln 2＝﹣1＋ln 2＜0，故排除选项B；
f(2)＝cs 2π＋ln 4＝1＋2ln 2＞0，故排除选项D.
已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(ex－1－1，x≤1，,lg2x，x>1，))则函数y＝f(1﹣x)的图象大致为( )

【答案解析】答案为：B
解析：函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(ex－1－1，x≤1，,lg2x，x>1，))所以y＝g(x)＝f(1﹣x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(e－x－1，x≥0，,lg21－x，x<0，))所以当x＝0时，g(0)＝e0﹣1＝0，故选项A，C错误；
当x≥0时，g(x)＝e﹣x﹣1单调递减，故选项D错误，选项B正确.
为了得到函数y＝lgeq \f(x＋3,10)的图象，只需把函数y＝lg x的图象上所有的点( )
A.向左平移3个单位长度，再向上平移1个单位长度
B.向右平移3个单位长度，再向上平移1个单位长度
C.向左平移3个单位长度，再向下平移1个单位长度
D.向右平移3个单位长度，再向下平移1个单位长度
【答案解析】答案为：C
解析：∵y＝lg eq \f(x＋3,10)＝lg(x＋3)﹣1，∴y＝lg xeq \(――――――――――→,\s\up7(向左平移3个单位长度 ))y＝lg(x＋3)eq \(――――――――――→,\s\up7(向下平移1个单位长度 ))y＝lg(x＋3)﹣1.
已知函数f(x)的图象如图所示，则函数f(x)的解析式可能是( )
A.f(x)＝(4x﹣4﹣x)|x| B.f(x)＝(4x﹣4﹣x)lg2|x|
C.f(x)＝eq \f(4x＋4－x,|x|) D.f(x)＝(4x＋4﹣x)lg2|x|
【答案解析】答案为：D
解析：由图知，f(x)为偶函数，故排除A，B；对于C，f(x)＞0不符合图象，故排除C；对于D，f(﹣x)＝(4x＋4﹣x)lg2|x|＝f(x)为偶函数，且在区间(0,1)上，f(x)＜0，符合题意.
已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(21－x，x≥1，,2x－1，x<1，))若f(2x﹣2)≥f(x2﹣x＋2)，则实数x的取值范围是( )
A.[﹣2，﹣1] B.[1，＋∞)
C.(﹣∞，﹣1]∪[2，＋∞) D.(﹣∞，﹣2]∪[1，＋∞)
【答案解析】答案为：D
解析：作出f(x)的图象，如图所示，
由图知f(x)的图象关于直线x＝1对称且在(﹣∞，1)上单调递增，在(1，＋∞)上单调递减，
∴|2x﹣2﹣1|≤|x2﹣x＋2﹣1|，即|2x﹣3|≤|x2﹣x＋1|＝x2﹣x＋1，
∴eq \b\lc\{\rc\ (\a\vs4\al\c1(2x－3≤x2－x＋1，,2x－3≥－x2＋x－1，))解得x≥1或x≤﹣2.
若平面直角坐标系内A，B两点满足：(1)点A，B都在f(x)的图象上；(2)点A，B关于原点对称，则称点对(A，B)是函数f(x)的一个“和谐点对”，(A，B)与(B，A)可看作一个“和谐点对”.已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x2＋2x，x<0，,\f(2,ex)，x≥0，))则f(x)的“和谐点对”有( )
A.1个 B.2个 C.3个 D.4个
【答案解析】答案为：B
解析：作出函数y＝x2＋2x(x＜0)的图象关于原点对称的图象(如图中的虚线部分)，看它与函数y＝eq \f(2,ex)(x≥0)的图象的交点个数即可，观察图象可得交点个数为2，即f(x)的“和谐点对”有2个.
二、多选题
(多选)对于函数f(x)＝lg(|x﹣2|＋1)，下列说法正确的是( )
A.f(x＋2)是偶函数
B.f(x＋2)是奇函数
C.f(x)在区间(﹣∞，2)上单调递减，在区间(2，＋∞)上单调递增
D.f(x)没有最小值
【答案解析】答案为：AC
解析：f(x＋2)＝lg(|x|＋1)为偶函数，A正确，B错误.作出f(x)的图象如图所示，可知f(x)在(﹣∞，2)上单调递减，在(2，＋∞)上单调递增；由图象可知函数存在最小值0，C正确，D错误.
(多选)关于函数f(x)＝|ln |2﹣x||，下列描述正确的有( )
A.函数f(x)在区间(1,2)上单调递增
B.函数y＝f(x)的图象关于直线x＝2对称
C.若x1≠x2，f(x1)＝f(x2)，则x1＋x2＝4
D.函数f(x)有且仅有两个零点
【答案解析】答案为：ABD.
解析：作出函数f(x)＝|ln |2﹣x||的图象如图所示，由图可得，函数f(x)在区间(1,2)上单调递增，A正确；函数y＝f(x)的图象关于直线x＝2对称，B正确；若x1≠x2，f(x1)＝f(x2)，则x1＋x2的值不一定等于4，C错误；函数f(x)有且仅有两个零点，D正确.
(多选)已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x2－3x，x≥0，,－e－x＋1，x<0，))方程|f(x)﹣1|＝2﹣m(m∈R)，则下列判断正确的是( )
A.函数f(x)的图象关于直线x＝eq \f(3,2)对称
B.函数f(x)在区间(3，＋∞)上单调递增
C.当m∈(1,2)时，方程有2个不同的实数根
D.当m∈(﹣1,0)时，方程有3个不同的实数根
【答案解析】答案为：BC
解析：对于选项A，f(4)＝4，f(﹣1)＝1﹣e，显然函数f(x)的图象不关于直线x＝eq \f(3,2)对称；对于选项B，f(x)＝x2﹣3x的图象是开口向上的抛物线，所以函数f(x)在区间(3，＋∞)上单调递增，作出函数y＝|f(x)﹣1|的图象，如图，
对于选项C，当m∈(1,2)时，2﹣m∈(0,1)，结合图形可知方程|f(x)﹣1|＝2﹣m(m∈R)有2个不同的实数根；
对于选项D，当m∈(﹣1,0)时，2﹣m∈(2,3)，结合图形可知方程|f(x)﹣1|＝2﹣m(m∈R)有4个不同的实数根.
(多选)在平面直角坐标系Oxy中，如图放置的边长为2的正方形ABCD沿x轴滚动(无滑动滚动)，点D恰好经过坐标原点，设顶点B(x，y)的轨迹方程是y＝f(x)，则对函数y＝f(x)的判断正确的是( )
A.函数y＝f(x)是奇函数
B.对任意x∈R，都有f(x＋4)＝f(x﹣4)
C.函数y＝f(x)的值域为[0,2eq \r(2)]
D.函数y＝f(x)在区间[6,8]上单调递增
【答案解析】答案为：BCD
解析：由题意得，当﹣4≤x＜﹣2时，点B的轨迹为以(﹣2,0)为圆心，2为半径的eq \f(1,4)圆；当﹣2≤x＜2时，点B的轨迹为以原点为圆心，2eq \r(2)为半径的eq \f(1,4)圆；
当2≤x＜4时，点B的轨迹为以(2,0)为圆心，2为半径的eq \f(1,4)圆，如图所示.
以后依次重复，所以函数f(x)是以8为周期的周期函数，由图象可知，函数f(x)为偶函数，故A错误；
因为f(x)的周期为8，所以f(x＋8)＝f(x)，即f(x＋4)＝f(x﹣4)，故B正确；
由图象可知，f(x)的值域为[0,2eq \r(2)]，故C正确；
由图象可知，f(x)在[﹣2,0]上单调递增，因为f(x)在[6,8]的图象和在[﹣2,0]的图象相同，故D正确.
三、填空题
已知函数y＝f(﹣x)的图象过点(4,2)，则函数y＝f(x)的图象一定过点________.
【答案解析】答案为：(﹣4,2)
解析：y＝f(﹣x)与y＝f(x)的图象关于y轴对称，故y＝f(x)的图象一定过点(﹣4,2).
若函数f(x)＝eq \f(ax－2,x－1)的图象关于点(1,1)对称，则实数a＝________.
【答案解析】答案为：1
解析：f(x)＝eq \f(ax－a＋a－2,x－1)＝a＋eq \f(a－2,x－1)，关于点(1，a)对称，故a＝1.
已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x2＋2x－1，x≥0，,x2－2x－1，x<0，))则对任意x1，x2∈R，若x2＞0＞x1＞﹣x2，则f(x1)与f(x2)的大小关系是________.
【答案解析】答案为：f(x1)＜f(x2)
解析：作出函数f(x)的图象(图略)，由图知f(x)为偶函数，且在(﹣∞，0)上单调递减，在(0，＋∞)上单调递增，∵0＞x1＞﹣x2，∴f(x1)＜f(﹣x2)＝f(x2).
已知函数f(x)＝|x﹣2|＋1，g(x)＝kx.若方程f(x)＝g(x)有两个不相等的实根，则实数k的取值范围是__________.
【答案解析】答案为：(eq \f(1,2)，1).
解析：先作出函数f(x)＝|x﹣2|＋1的图象，如图所示，当直线g(x)＝kx与直线AB平行时斜率为1，当直线g(x)＝kx过A点时斜率为eq \f(1,2)，故f(x)＝g(x)有两个不相等的实根时，k的取值范围为(eq \f(1,2)，1).
四、解答题
分别作出下列函数的图象：
(1)y＝|lg x|；(2)y＝2x＋2；(3)y＝x2﹣2|x|﹣1.
【答案解析】解：(1)y＝eq \b\lc\{\rc\ (\a\vs4\al\c1(lg x， x≥1，,－lg x， 0(2)将y＝2x的图象向左平移2个单位.图象如图②所示.
(3)y＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x2－2x－1，x≥0，,x2＋2x－1，x<0.))图象如图③所示.
已知函数
f(x)=eq \b\lc\{\rc\ (\a\vs4\al\c1(3－x2，x∈[－1，2]，,x－3，x∈2，5].))
(1)在如图所示给定的直角坐标系内画出f(x)的图象；
(2)写出f(x)的单调递增区间；
(3)由图象指出当x取什么值时f(x)有最值．
【答案解析】解：
(1)函数f(x)的图象如图所示．
(2)由图象可知，函数f(x)的单调递增区间为[-1，0]，[2，5]．
(3)由图象知当x=2时，f(x)min=f(2)=-1，
当x=0时，f(x)max=f(0)=3.
已知函数f(x)=2x，x∈R.
(1)当m取何值时，方程|f(x)－2|=m有一个解？两个解？
(2)若不等式[f(x)]2＋f(x)－m＞0在R上恒成立，求m的取值范围.
【答案解析】解：(1)令f(x)=|f(x)－2|=|2x－2|，G(x)=m，画出f(x)的图象如图所示.
由图象看出，当m=0或m≥2时，函数f(x)与G(x)的图象只有一个交点，
即原方程有一个解；
当0＜m＜2时，函数f(x)与G(x)的图象有两个交点，即原方程有两个解.
(2)令f(x)=t(t＞0)，H(t)=t2＋t，
因为H(t)=eq \b\lc\(\rc\)(\a\vs4\al\c1(t＋\f(1,2)))2－eq \f(1,4)在区间(0，＋∞)上是增函数，所以H(t)＞H(0)=0.
因此要使t2＋t＞m在区间(0，＋∞)上恒成立，应有m≤0，
即所求m的取值范围为(－∞，0].
已知函数f(x)＝2x，x∈R.
(1)当m取何值时方程|f(x)﹣2|＝m有一个解？
(2)若不等式[f(x)]2＋f(x)﹣m＞0在R上恒成立，求m的取值范围.
【答案解析】解：(1)令F(x)＝|f(x)﹣2|＝|2x﹣2|，G(x)＝m，画出F(x)的图象如图所示.
由图象看出，当m＝0或m≥2时，函数F(x)与G(x)的图象只有一个交点，原方程有一个解，
故m的取值范围是{0}∪[2，＋∞).
(2)令f(x)＝t(t＞0)，H(t)＝t2＋t，
因为H(t)＝(t＋eq \f(1,2))2﹣eq \f(1,4)在区间(0，＋∞)上是增函数，
所以H(t)＞H(0)＝0.因此要使t2＋t＞m在区间(0，＋∞)上恒成立，应有m≤0，
即所求m的取值范围是(﹣∞，0].