初中人教版（2024）21.2.1 配方法教学ppt课件

这是一份初中人教版（2024）21.2.1 配方法教学ppt课件，共22页。PPT课件主要包含了学习目标，新课引入，新知学习，课堂小结，a+b，a-b，x2+6x+，a2±2ab+b2，+2·x·3，x+3等内容，欢迎下载使用。

1.运用配方法解二次项系数为1的一元二次方程.2.理解并掌握配方法的一般步骤.
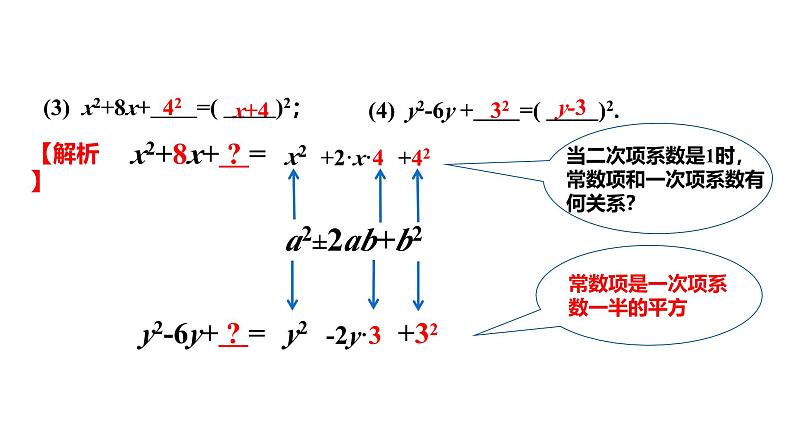
使下列各式是完全平方式
1.用直接开平方法解下列方程:
(1) (x-2)2=2 （2）9x2+12x+4=9
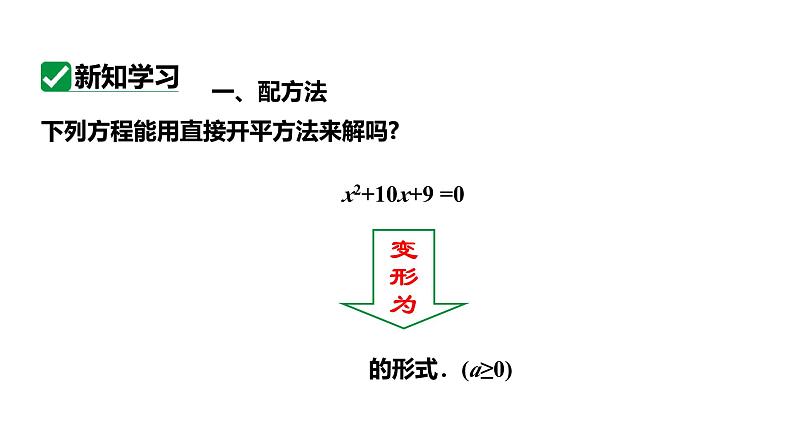
x2+10x+9 =0；
你能把方程化成(x+n)2=p(p≥0)的形式吗？
解： (3x+2)²=9 即 3x+2=±3
下列方程能用直接开平方法来解吗?
x2+10x+9 =0
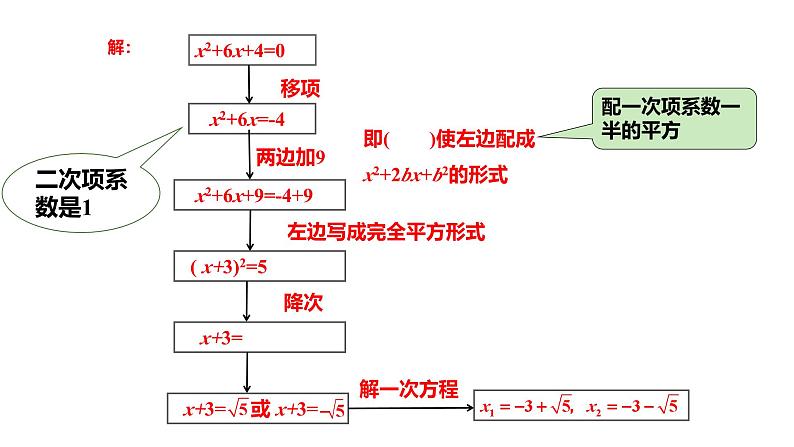
x2+6x=-4
x2+6x+9=-4+9
( x+3)2=5
配一次项系数一半的平方
x+3= 或 x+3=
配方法：通过配成完全平方形式来解一元二次方程的方法.
基本思路：将一般式ax²+bx+c=0（a≠0）转化为(x+n)2=p的形式， 再通过直接开平方法（降次），转化为一元一次方程求解．
分析：(1)方程的二次项系数为1，直接运用配方法.
(1)x2-8x+1=0
(2)2x2+1=3x
分析：先移项，将方程化为一般式，再将二次项系数化为1，然后用配方法解方程.
因为实数的平方不会是负数，所以x取任何实数时，上式都不成立，所以原方程无实数根．
(3)3x2-6x+4=0
分析：与(2)类似，将二次项系数化为1后再配方.
(4)x(x+4)=8x+12
配方法解一元二次方程的一般式步骤.
一移，化成一般式，把常数项移到等号右边；二化，二次项系数化为1；三配，方程两边都加上一次项系数一半的平方；四写，方程写成(x+n)2=p的形式；五开，方程两边开平方，得两个一元一次方程；六解，解一元一次方程；七定，写出原方程的根.
注意：p≥0，才有根
1.应用配方法求最值.(1) 2x2 - 4x+5的最小值； (2) -3x2 + 6x -7的最大值.
解：原式 = 2(x - 1)2 +3 当x =1时，有最小值3.
解：原式= -3(x - 1)2 - 4 当x =1时，有最大值-4.
1.用配方法解下列方程
2. 试用配方法说明：不论k取何实数，多项式 k2－2k＋4 的值必定大于零.
解：k2－2k＋4=k2－2k＋1＋3
因为(k－1)2≥0，所以(k－1)2＋3≥3.
所以k2－2k＋4的值必定大于零.
3.【阅读材料】若x²+y²＋8x-6y＋25=0，求x，y的值．解：(x2+8x+16)＋(y2-6y+9)=0，(x+4)2+(y-3)2=0，∴x+4=0，y-3=0.∴x=-4，y=3. 【解决问题】(1)已知m²＋n2-12n＋10m＋61=0，求(m＋n)2023的值；
解:(1)∵m²+n²-12n+10m+61=0，将61拆分为25和36，可得：（m²＋10m＋25）＋（n2-12n＋36）=0，根据完全平方公式得(m＋5)2＋(n-6)2=0，∴m＋5=0, n-6=0，∴m=-5，n=6，∴(m＋n)2023=(-5＋6)2023=1.
通过配成完全平方形式解一元二次方程的方法.
一化，二次项系数化为1，化成一般式后；二移，把常数项移到等号右边；三配，方程两边都加上一次项系数一半的平方；四写，方程写成(x+n)2=p的形式；五开，方程两边开平方，化成2个一元一次方程；六解，解一元一次方程；七定，写出原方程的根.