数学必修第二册1复数的三角形式优秀教学ppt课件

这是一份数学必修第二册1复数的三角形式优秀教学ppt课件，共33页。PPT课件主要包含了学习目标，复习引入，新知探究，课本例题，课本练习，随堂检测等内容，欢迎下载使用。
1.了解复数乘、除运算的三角表示（重点）2.了解复数乘、除运算及乘方、开方的几何意义3.会利用复数三角形式进行复数乘、除及乘方、开方运算（重点、难点）
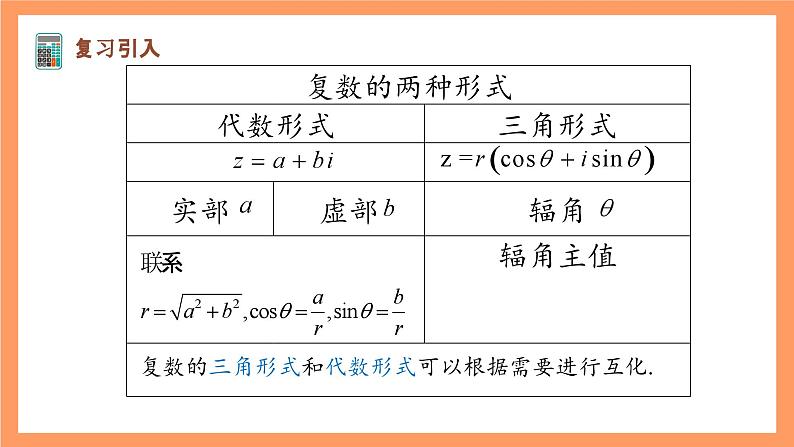
复数的三角形式和代数形式可以根据需要进行互化.
复数的代数形式的乘除运算法则
两角和（差）的正弦、余弦公式
现在我们讨论三角形式下的复数乘除运算公式． 设有两个用三角形式表示的复数 z1＝r（cs α＋isin α）与z２＝s（cs β＋isin β），其中r＝｜z１｜≥０，s＝｜z２｜≥０，则
1.三角形式下复数的乘除运算
也就是说，两个复数相乘，其积的模等于模的积，积的辐角等于辐角的和；两个复数相除（除数不为零），其商的模等于模的商，商的辐角等于辐角的差．
证明 乘积的公式的推导是两角和的正弦、余弦公式的直接应用：
再把等式两边同除以z２，就得到所求的除法公式．
例３ 计算，并用复数的代数形式表示计算结果：
——复数三角形式的乘法
两个复数三角形式相乘，把模相乘作为积的模，把辐角相加作为积的辐角，若遇到复数的代数形式与三角形式混合相乘时，需将相混的复数统一成代数形式或三角形式，然后再进行复数的代数形式相乘或三角形式相乘，当不要求把计算结果化为代数形式时，也可以用三角形式表示.
——计算时未化为标准三角形式
——复数三角形式的除法
两个三角形式的复数相除，则商还是一个复数，它的模等于被除数的模除以除数的模所得的商，它的辐角等于被除数的辐角减去除数的辐角所得的差.若出现复数的代数形式，先转化为复数的三角形式，再计算
我们现在来分析复数乘法的几何意义．
——复数乘法、除法的几何意义
——计算时未化为标准三角形式
2 三角形式下复数的乘方与开方
复数的n次幂（n是正整数）是n个相同复数的连乘，因此，根据复数乘法公式，一个复数的 n 次幂的模是底数模的 n 次幂，而其辐角是底数辐角的 n 倍．作为乘方的逆运算，自然会想到，一个复数开 n 次方，方根的模是被开方数模的 n 次方根，而方根的辐角是被开方数辐角的 n 分之一．这个规则原则上没错，但要注意的是：由于被开方数不同辐角的 n 分之一所得出的辐角可能有不同的主值， 在这个过程中被开方数的辐角不能只取主值．事实上，如果α是被开方数的辐角之一，以下 n 个值都可以作为被开方数 n 次方根的辐角：
例６ 求１的三次方根．
２．求１的所有四次方根．
2.复数(sin10°+ics10°)(sin10°+ics10°)的三角形式是( ____ )A.sin30°+ics30°B.cs160°+isin160°C.cs30°+isin30°D.sin160°+ics160°
【解析】解：(sin10°+ics10°)(sin10°+ics10°)=sin210°-cs210°+2sin10°cs10°i=-cs20°+sin20°i=cs160°+isin160°．故选：B．
3.已知平面直角坐标系xOy中向量的旋转和复数有关，对于任意向量x=(a,b)，对应复数z=a+bi,向量x逆时针旋转一个角度θ，得到复数z'=(a+bi)(csθ+isinθ)=acsθ-bsinθ+i(asinθ+bcsθ)，于是对应向量x'=(acsθ-bsinθ，asinθ+bcsθ)．这就是向量的旋转公式．已知正三角形ABC的两个顶点坐标是A(1，4)，B(3，2)，根据此公式，求得点C的坐标是 　　．(任写一个即可)
=(acsθ+bsinθ)+(bcsθ-asinθ)i.
易知，关于x的方程x2024-1=0的根为1，z,z2 …，z2023，故x2024-1=(x-1)(x-z)(x-z2)⋯(x-z2023)，又x2024-1=(x-1)(1+x+x2+x2023)，故(x-z)(x-z2)⋯(x-z2023)=1+x+⋯+x2023，令x=1，可得(1-z)(1-z2)⋯(1-z2023)=1+1+⋯+12023=2024，且2023为奇数，所以(z-1)(z2-1)⋯(z2022-1)=-2024．