





数学第9章 复数*9.4 复数的三角形式1复数的三角形式获奖教学ppt课件
展开1.了解复数三角表示式的推导过程,2.了解复数的三角表示式,3.了解复数的代数表示与三角表示之间的关系4.会进行复数三角形式和代数式之间的互换,5.了解两个用三角形是表示的复数相等的条件
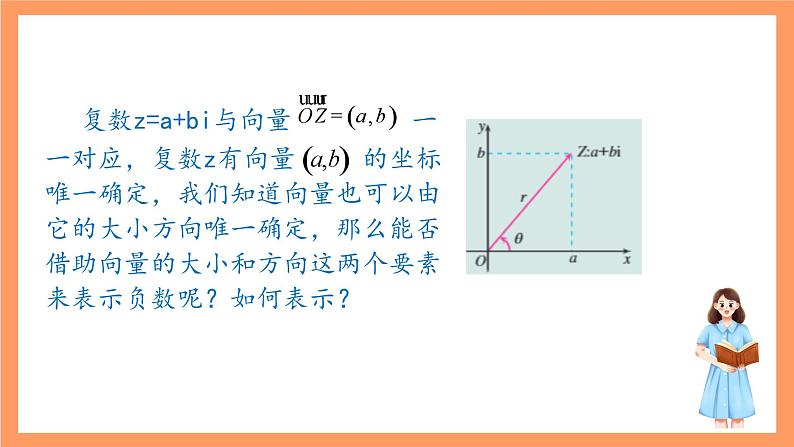
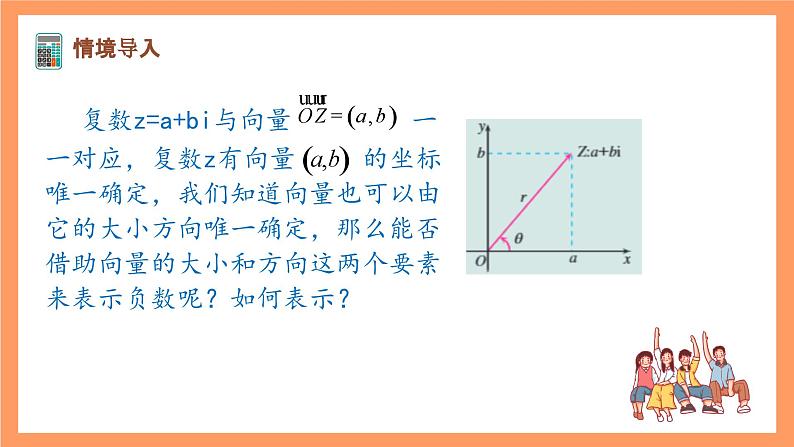
复数z=a+bi与向量 一一对应,复数z有向量 的坐标唯一确定,我们知道向量也可以由它的大小方向唯一确定,那么能否借助向量的大小和方向这两个要素来表示负数呢?如何表示?
思考:你能用向量 的模和角 来表示负数z吗?
记向量的模 由图可以得到:
这样,我们就用刻画向量大小的模 和刻画向量方向的角 表示复数z.
一般的任何一个复数z=a+bi都可以表示成 形式,其中 是复数的模, 是以x轴的非负半轴的始边,向量 所在射线为终边的角,叫做复数z=a+bi的 , , 叫做复数的三角形式,简称三角形式。为了与三角形式区分开来 叫做复数的代数表示式,简称代数形式
任何一个不为零的复数的辐角有无限多个,且这些值相差 整数倍
规定在 范围内的辐角 的值为辐角主值,通常记作
规定:复数0的辐角的大小是任意的值.
例1 分别写出下列复数的模与辐角主值θ,并把这些复数用三角形式表示:
例2 把下列复数用三角形式表示:
解 (1)因为cs(-θ)=csθ,sin(-θ)=-sinθ,所以csθ-isinθ的三角形式是cs(-θ)+isin(-θ)
(2)-2(cs α+isin α)的模是2.又因为cs(π+α)= -cs α,sin(π+α)=-sin α,所以-2(cs α+isin α)的三角形式是2[cs(π+α)+isin(π+α)]
【巩固练习2】把下列复数转化为三角形式
①先求复数的模②确定辐角的终边所在 的象限③根据辐角终边的位置 求出辐角④求出复数的三角形式
【巩固练习3】下列复数是不是三角形式?如果不是,请把它表示成三角形式.
【解】(1)由“角相同”知,不是三角形式;
把复数从三角形式转化成代数形式,直接求出角的三角函数值,化简即可
练习9.4(1)1.下列复数是否用三角形式来表示的?为什么?
2.把下列复数用三角形式表示(用辐角主值)
5.复数1+i的辐角主值是 .
6.复数sin1-ics1的辐角主值是 .
数学必修第二册1复数的三角形式优秀教学ppt课件: 这是一份数学必修第二册<a href="/sx/tb_c4056175_t3/?tag_id=26" target="_blank">1复数的三角形式优秀教学ppt课件</a>,共33页。PPT课件主要包含了学习目标,复习引入,新知探究,课本例题,课本练习,随堂检测等内容,欢迎下载使用。
高中1复平面与复数的坐标表示获奖教学ppt课件: 这是一份高中<a href="/sx/tb_c4056167_t3/?tag_id=26" target="_blank">1复平面与复数的坐标表示获奖教学ppt课件</a>,共20页。PPT课件主要包含了复数的模的几何意义,什么是复平面等内容,欢迎下载使用。
高中沪教版(2020)1复平面与复数的坐标表示完整版教学课件ppt: 这是一份高中沪教版(2020)<a href="/sx/tb_c4056167_t3/?tag_id=26" target="_blank">1复平面与复数的坐标表示完整版教学课件ppt</a>,共21页。PPT课件主要包含了学习目标,复习引入,情境导入,新课讲解,复数的几何意义1,课本例题,一一对应,复数的几何意义2,2复数的向量表示,补充例题等内容,欢迎下载使用。













