初中数学湘教版（2024）九年级下册1.1 二次函数课前预习课件ppt

这是一份初中数学湘教版（2024）九年级下册1.1 二次函数课前预习课件ppt，共24页。PPT课件主要包含了逐点导讲练，课堂小结，作业提升，学习目标，课时讲解，课时流程，感悟新知，知识点，解列表等内容，欢迎下载使用。
二次函数 y=ax2 的图象的画法二次函数 y=ax2 的图象与性质
二次函数 y=ax2 的图象的画法
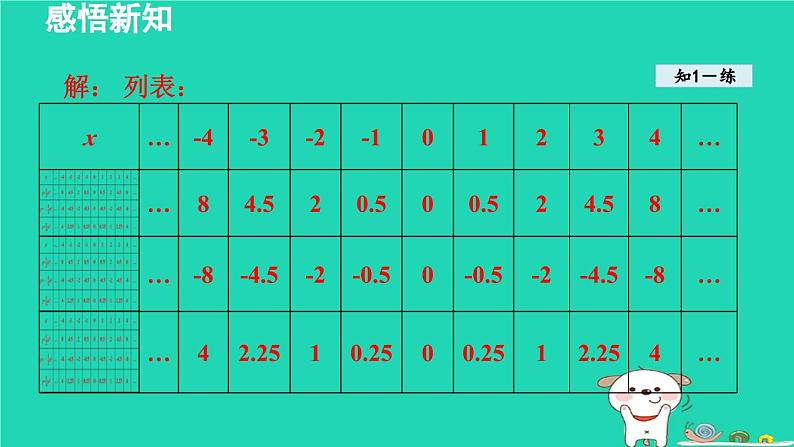
用描点法画函数 y=ax2( a ≠ 0)的图象的一般步骤(1) 列表：列表时，自变量 x 的取值不能太大也不能太小，以便于描点和全面反映图象情况 .选点时，一般先找出对称轴，再在对称轴两侧对称选取，应以计算简单、描点方便为原则 .
(2) 描点：一般来说，点取得越多、越密集，画出的图象就越准确 .实际画图时，一般取顶点及对称轴两侧对称的两对点，共 5 个点，用“五点法”快速准确地作出函数图象 .(3) 连线：按自变量由小到大(或由大到小)的顺序，依次用光滑的曲线连接各点 .
特别提醒◆用描点法可以画出任意一个二次函数的图象，用描点法画出的图象只是二次函数图象的一部分 .◆抛物线是向两方无限延伸的，画图时要画“出头”，左右两侧必须保持关于对称轴对称 .
解题秘方：用描点法，按列表→描点→连线的顺序作图 .
解法警示在同一平面直角坐标系中作多个函数图象时，要在图象旁边标明函数的表达式 .连线时，必须按照自变量由小到大 (或由大到小 ) 的顺序，并且用光滑的曲线顺次连接，初始点和末端点处要注意适当“向外延伸”，切忌用线段连接或漏点、跨点连接 .
描点、 连线，即得三个函数的图象，如图 1.2-1.
二次函数 y=ax2 的图象与性质
1. 把二次函数 y=ax2的图象这样的曲线叫作抛物线，简称为抛物线 y=ax2. 一般地，二次函数 y=ax2的图象关于 y 轴对称，抛物线与它的对称轴的交点( 0，0)叫作抛物线y=ax2的顶点 .
2.二次函数 y=ax2 (a ≠ 0)的图象与性质
要点解读1. 判断二次函数的增减性的技巧：从抛物线的对称轴分开，自左向右看， “上坡路”就是 y 随 x 的增大而增大，“下坡路”就是y随x的增大而减小.2. 在二次函数y=ax2(a ≠ 0) 中，a 的正负性决定抛物线的开口方向，|a| 决定抛物线的开口大小．|a|越大，抛物线开口越小，反之，|a| 越小，抛物线开口越大．3. 二次函数 y=－ax2(a≠0)与y=ax2( a≠0)的图象关于 x 轴对称 .
如图 1.2-2， 四个二次函数的图象分别对应① y=ax2；② y=bx2；③ y=cx2；④ y=dx2，已知①与③、②与④分别关于 x 轴对称 .
解题秘方：紧扣 “a 的符号”及“|a| 的大小”与其图象之间的关系采用数形结合思想进行解答 .
方法点拨y=ax2中 a 与其图象开口方向、开口大小之间的关系：1. a 的符号：a>0 ↔开口向上；a0， b>0， c|d|， ∴ a>b，cb>d>c.
巧题妙解当 x=1 时，四个函数值分别等于二次项系数，∴直线 x=1 与四条抛物线的交点从上到下依次为(1，a)，(1，b)，(1，d)，(1，c)，∴ a>b>d>c.
(2)说明 a 与 c， b 与 d 的数量关系 .
解：∵①与③，②与④分别关于 x 轴对称，∴①与③，②与④的开口大小相同，方向相反 .∴ a+c=0， b+d=0.
[易错题]已知函数 y= (m+2) xm²+m-4 是关于 x 的二次函数 .
解题秘方：按对称轴的左、右两侧，分 x ＞ 0 和 x ＜ 0两种情况讨论函数的增减性 .
(1)求满足条件的 m 的值 .
解：由题意得 m2+m-4=2， m+2 ≠ 0， 解得 m=2 或 m= － 3.∴满足条件的 m 的值为 2 或－3.
注意二次项系数不为 0.
(2)当 m 为何值时，其图象有最低点？求出这个最低点的坐标，这时当 x 为何值时， y 随 x 的增大而增大？
解：若抛物线有最低点，则抛物线的开口向上，∴ m+2>0，即 m> － 2. ∴ m=2.∵这个最低点为抛物线的顶点，∴最低点的坐标为(0，0) .当 x>0 时， y 随 x 的增大而增大 .
(3)当 m 为何值时，函数有最大值？最大值是多少？这时当 x 为何值时， y 随 x 的增大而减小？
解：若函数有最大值，则抛物线的开口向下，∴ m+20 时， y 随 x 的增大而减小 .
解法提醒在分析二次函数的增减性时，都是以对称轴为分界线进行讨论的：1. 开口向下的抛物线，在对称轴左侧， y 随 x的增大而增大，在对称 轴右侧， y 随 x 的增大而减小；2. 开口向上的抛物线，在对称轴左侧， y 随 x的增大而减小，在对称 轴右侧， y 随 x 的增大而增大 .