湘教版九年级下册1.1 二次函数课前预习ppt课件

这是一份湘教版九年级下册1.1 二次函数课前预习ppt课件，共26页。PPT课件主要包含了-3x2等内容，欢迎下载使用。

1.理解具体情景中二次函数的意义，理解二次函数的概念,掌握二次函数的一般形式.2.能够表示简单变量之间的二次函数关系式,并能根据实际问题确定自变量的取值范围.3.经历探索,分析和建立两个变量之间的二次函数关系的过程,进一步体验如何用数学的方法描述变量之间的数量关系.4.体会数学与实际生活的密切联系,学会与他人合作交流,培养合作意识.【教学重点】二次函数的概念.【教学难点】在实际问题中,会写简单变量之间的二次函数关系式教学过程.
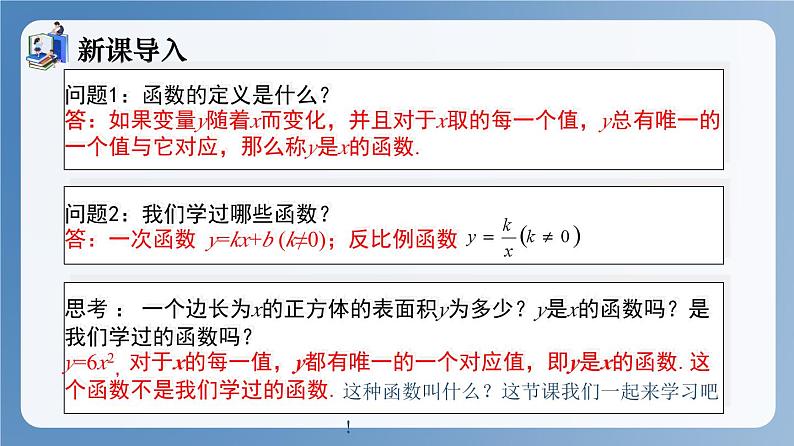
问题1：函数的定义是什么？答：如果变量y随着x而变化，并且对于x取的每一个值，y总有唯一的一个值与它对应，那么称y是x的函数.
思考 ： 一个边长为x的正方体的表面积y为多少？y是x的函数吗？是我们学过的函数吗？y=6x2，对于x的每一值，y都有唯一的一个对应值，即y是x的函数.这个函数不是我们学过的函数.
这种函数叫什么？这节课我们一起来学习吧！
1.学校准备在校园里利用围墙的一段和篱笆墙围成一个矩形植物园，已知篱笆墙的总长度为 100 m，设与围墙相邻的每一篱笆墙的长度都为 x（m），求矩形植物园的面积 S（m2）与 x 之间函数关系式.
对于x的每一个取值，S都有唯一确定的值与它对应，即S是x的函数.
2.某型号的电脑两年前的销售为 6000 元，现降价销售，若每年的平均降价率为 x，求现在售价y （元）与平均降价率 x 之间的函数关系.
观察上面所列的函数表达式有什么共同点？它们与一次函数的表达式有什么不同？
观察左边的函数表达式①②有什么共同点？它们与一次函数的表达式有什么不同？
都是关于自变量的二次多项式
定义：如果函数的表达式是自变量的二次多项式，那么，这样的函数称为二次函数，它的一般形式是y=ax2+bx+c ( a， b， c 是常数， a ≠ 0 ). 其中 x 是自变量， a， b， c 分别是函数表达式的二次项系数、一次项系数和常数项．
特别解读二次函数的特殊形式：(1)只含二次项，即：y=ax2(b=0，c=0)；(2)不含一次项，即：y=ax2+c(b=0，c≠0)；(3)不含常数项，即：y=ax2+bx(b ≠ 0，c=0).
2. 确定二次函数的“三要素”(1)含有自变量的代数式必须是整式；(2)化简后自变量的最高次数是 2；(3)二次项系数不等于0 .
“三要素”要牢记，这是确定二次函数的关键 .
1、指出下列函数中哪些是二次函数.
（1） （2） （3） （4） （5）
判定一个函数是否为二次函数的思路:1.将函数化为一般形式.2.自变量的最高次数是 2 次.3.若二次项系数中有字母, 二次项系数不能为 0.
第（2）问易忽略二次项系数a≠0这一限制条件，从而得出m=3或-3的错误答案，需要引起同学们的重视
【例2】如图，一块矩形木板，长为120cm、宽为80cm，在木板4个角上各截去边长为x(cm)的正方形，求余下面积S(cm2)与x之间的函数表达式.
注意：二次函数的自变量的取值范围是所有实数，但在实际问题中，它的自变量的取值范围会有一些限制.即要满足题意。
分析：本问题中的数量关系是：
木板余下面积 = 矩形面积 - 截去面积.
解：木板余下面积 S 与截去正方形边长 x 有如下函数关系： S = 120×80 - 4×x2 = - 4x2 + 9 600 ， 0 ＜ x ≤ 40 .
建立二次函数模型的一般步骤 (1)审清题意：找出问题中的已知量(常量)和未知量(变量) ，把问题中的文字或图形语言转化成数学语言 .(2)找相等关系 ：分析常量和变量之间的关系，列出等式 .
(3)列二次函数表达式： 设出表示变量的字母，把相等关系用含字母的式子表示，并整理成二次函数的一般形式 .(4) 确定函数自变量的取值范围： 二次函数的自变量在一般情况下是没有条件限制的，即自变量可以取一切实数，但是在实际问题中，变量都有一定的实际意义，会受到一定的条件限制，所以在求出二次函数的表达式后，还要指明自变量的取值范围 .
特别提醒1. 建立二次函数模型与建立一元二次方程模型类似，不同的是需将它转化为用含一个未知数(自变量)的代数式表示另一个未知数(函数)的形式 .2. 自变量的取值范围应使实际问题有意义 .
2.一个正方形的边长是12cm，若从中挖去一个长为2xcm，宽为(x+1)cm的小长方形．剩余部分的面积为ycm2.写出y与x之间的函数关系式，并指出y是x的什么函数？
分析：本题中的数量关系是： 剩余面积=正方形面积-长方形面积.
解：由题意得y＝122－2x(x+1)， 又∵x+1<2x≤12，∴1方法点拨：在实际问题中建立二次函数模型时，关键要找出两个变量之间的数量关系，用类似建立一元二次方程模型的方法，借助方程思想求出二次函数的表达式 .
1. 药店决定对某药物价格分两次降价,若设平均每次降价 的百分率为 x, 该药品的原价为 36 元, 降价后的价格 为 y 元, 则 y 与 x 之间的函数表达式为（ ） A．y＝72(1－x) B．y＝ 36(1－2x) C．y＝36(1－x2) D．y＝ 36(1－x)2
3、下列函数中,哪些是二次函数?若是请指出二次项系数，一次项系数和常数项
二次项系数为1，一次项系数和常数项均为0
二次项系数为-1，一次项系数为1，常数项为0
4、把y=(2-3x)(6+x)变成一般式，二次项为_____,一次项系数为______，常数项为 .
5、函数 y=(m-n)x2+ mx+n 是二次函数的条件是( ) A . m,n是常数,且m≠0 B . m,n是常数,且n≠0 C. m,n是常数,且m≠n D . m,n为任何实数
6、当m 取何值时，函数y=（m2+m）xm2-2m-1+（m-5）x+m2是关于x 的二次函数？并求出二次函数的解析式.
满足二次函数的条件是什么？1.x的最高次是2；2.二次项系数不为0.
7. 如图为一隧道的截面示意图， 它的上部是一个半圆，下部是一个矩形， 且矩形的竖直的边长为 2.5 m. 设隧道截面积为 S（m2）， 截面半圆的半径为 r（m），试写出 S 关于 r 的函数表达式．
一般地，形如 y=ax²+bx+c ( a，b，c是常数，a≠ 0 ) 的函数叫做二次函数. 其中， x 是自变量，a，b，c 分别是函数解析式的二次项系数、一次项系数和常数项.(最高次是2次；二次项系数a≠0)
y=ax2+bx+c(a,b,c是常数，a ≠0，）
y=ax2 (a ≠0)；y=ax2+bx(a ≠0)；y=ax2+c(a ≠0，a,b,c是常数).
1.教材P4第1~3题. 2.完成同步练习册中本课时的练习.