

广东省广州市黄广中学2024-2025学年八年级上学期10月月考数学试卷
展开命题人:刘景锋 初审:万修权 终审:殷玉莲
试卷满分:120分 考试时长:120分钟
一、选择题:本题共10小题; 每小题3分,共30分。
1.下列长度的三条线段能组成三角形的是( )
A.3, 4, 8 B.5, 6, 11 C.5, 6, 10 D.1, 2, 3
2.如图, AD是△ABC的角平分线, 则( )
A.∠1=12∠BAC B.∠1=12∠ABC C.∠1=∠BAC D.∠1 =∠ABC
3.如图,一名工作人员不慎将一块三角形模具打碎成三块,他要带其中一块或两块碎片到商店去配一块与原来一样的三角形模具,他带( )去最省事A.①B.② C.③ D.①③
4.若一个多边形的内角和为540°,则这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
5.在数学实践课上,小亮经研究发现:在如图所示的△ABC中,连接点A和BC上的一点D,线段AD等分△ABC的面积, 则AD是△ABC的( ) A.高线 B.中线C.角平分线D.对角线
6.从十边形的一个顶点出发可以画出的对角线的条数是( )
A.7 B.8 C.9 D.10
7.若△DEF≌△ABC, ∠A =70°, ∠B =50°, 点A的对应是D, AB = DE, 则∠F的度数是( )
A.70° B.60° C.50° D.以上都不对
第1页,共6页8.如图, 已知△ABC中, ∠B=50°, 若沿图中虚线剪去∠B, 则∠1+∠2等于( )
A.130°D.310°
C.270°
B.230°
9.如图, 已知∠1=∠2, 则不一定能使△ABD≌△ACD的条件是( )
A. BD =CD B. AB=AC C.∠B =∠C D.∠BDA=∠CDA
10.如图, 在△ABC中, AB =AC, BD为AC边上的高, BE平分∠ABD, 点F在BD上, 连接EF并延长交BC于点G, 若BG=EG, ∠A=2∠DEF, 有下列结论: ①∠DEF =∠CBD; ②∠ABE+∠CBD =45°; ③EG⊥BC; ④BF=CE.其中正确的结论有( ) A.1个 B.4个 C.3个 D.2个
二、填空题:本题共6小题,共18分。
(11 题) 11.如图, 点D是△ ABC的边CB延长线上一点, 若∠ABD =100°, ∠A =60°, 则∠C= .
12.如图2, PM⊥OA, ∠POA=∠POB, PM=1, 当点P到OB的距离为 .
13.如图, 在△ABC中, ∠C=90°, AC=3, BC=4, AB=5, 则点C到AB的距离为 .
14.如图, △ABC≌△DEC, CA和CD, CB和CE是对应边, ∠ACD =28°, 则∠BCE = °.
15.如图, 在Rt△ABC中, ∠ABC=90°, D是CB延长线上的一点, BD =BA, DE⊥AC于点E,交AB于点F.若DC =7.8, BF=3, 则AF的长为 .
(15题图)
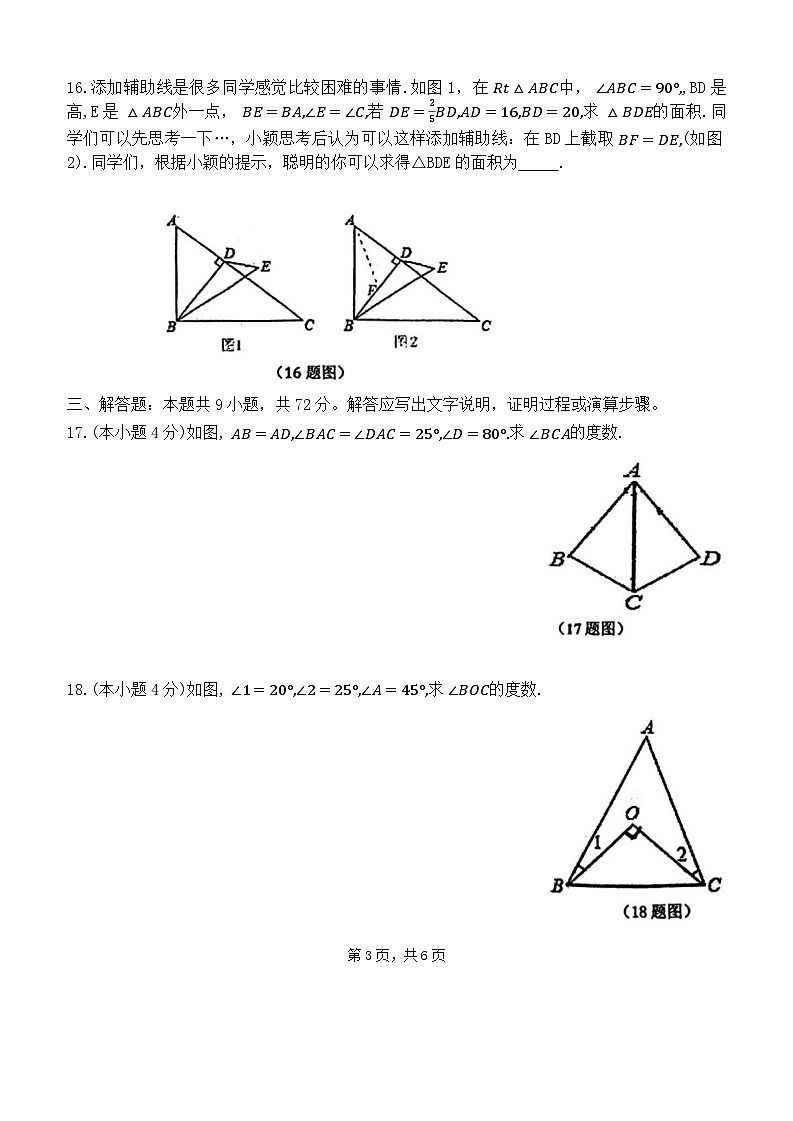
第2页,共6页16.添加辅助线是很多同学感觉比较困难的事情.如图1,在 Rt△ABC中, ∠ABC=90°,,BD是高,E是 △ABC外一点, BE=BA,∠E=∠C,若 DE=25BD,AD=16,BD=20,求 △BDE的面积.同学们可以先思考一下…,小颖思考后认为可以这样添加辅助线:在BD上截取 BF=DE,(如图2).同学们,根据小颖的提示,聪明的你可以求得△BDE的面积为 .
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题4分)如图, AB=AD,∠BAC=∠DAC=25°,∠D=80°.求 ∠BCA的度数.
18.(本小题4分)如图, ∠1=20°,∠2=25°,∠A=45°,求 ∠BOC的度数.
第3页,共6页19.(本小题6分)如图, B是AD的中点, BC‖DE,BC=DE
求证: ∠C=∠E.
20.(本小题6分)如图, AD, BE分别是 △ABC的高. 若 AD=4,BC=6,AC=5,,求BE的长.
21.(本小题8分)如图, 已知点C, D都在线段BF上, BD=CF,AC//DE,∠A=∠E.
(1)求证: △ABC≅△EFD;
(2)求证: AB‖EF.
22.(本小题10分)如图, 在 △ABC中, ∠ABC=∠BAC=30°,∠ADC=90°.
(1)画图:过点A画BC的垂线,交BC的延长线于点E.(保留画图痕迹,不要求画法)(21题图) (2)求证: AD=AE.
(22题图)23.(本小题10 分)如图, 在 △ABC中, BC=6,AB=2,
(1)若AC是偶数, 求AC的长;
(2)已知BD是 △ABC的中线,若 △ABD的周长为9,求△BCD的周长.
(23题图)
24.(本小题12分)
在 △ABC中, AB=AC,,点D在射线BA上,点E在AC的延长线上,且 BD=CE.连接DE, DE与BC边所在的直线交于点F.
(1)当点D在线段BA上时,如图所示,求证: DF=EF.
(2)过点D作 DH⊥BC交直线BC于点H.若 BC=4,CF=1,,求BH的长是多少?
第5页,共6页25.(本小题12分)
(1)如图1, 在△ABC中, AB=4,AC=6,,AD是BC边上的中线,延长AD到点E使 DE=AD,连接CE, 把AB、AC、2AD集中在△ACE中,利用三角形三边关系可得AD的取值范围是 ;
(2)如图2, 在 △ABC中, AD是BC边上的中线, 点E、F分别在AB、AC上, 且 DE⊥DF,求证:BE+CF> EF;
(3)如图3, 在四边形ABCD中, ∠A为钝角,∠C为锐角, ∠B+∠ADC=180°,DA=DC,点E、F分别在BC、AB上, 且 ∠EDF=12∠ADC,连接EF,试探索线段AF、EF、CE之间的数量关系,并加以证明.
第6页,共6页
广东省广州市黄广中学2024~2025学年七年级上学期数学10月月考试卷(无答案): 这是一份广东省广州市黄广中学2024~2025学年七年级上学期数学10月月考试卷(无答案),共4页。试卷主要包含了2023的倒数是,关于x的方程的解是,则a的值为,下列计算正确的是,如图,一副三角板等内容,欢迎下载使用。
广东省广州市黄广中学2023-—2024学年下学期期中考试七年级数学试卷: 这是一份广东省广州市黄广中学2023-—2024学年下学期期中考试七年级数学试卷,共6页。
广东省广州市黄广中学2023-—2024学年下学期期中考试七年级数学试卷+: 这是一份广东省广州市黄广中学2023-—2024学年下学期期中考试七年级数学试卷+,共6页。












