人教版（2024）九年级上册22.1.1 二次函数精品学案

这是一份人教版（2024）九年级上册22.1.1 二次函数精品学案，文件包含专题227二次函数中的最值问题八大题型举一反三人教版原卷版docx、专题227二次函数中的最值问题八大题型举一反三人教版解析版docx等2份学案配套教学资源，其中学案共86页， 欢迎下载使用。


TOC \ "1-3" \h \u
\l "_Tc17744" 【题型1 几何图形中线段最值问题】 PAGEREF _Tc17744 \h 1
\l "_Tc1983" 【题型2 两线段和的最值问题】 PAGEREF _Tc1983 \h 2
\l "_Tc25836" 【题型3 周长的最值问题】 PAGEREF _Tc25836 \h 4
\l "_Tc31085" 【题型4 面积的最值问题】 PAGEREF _Tc31085 \h 6
\l "_Tc11133" 【题型5 线段和差倍分的最值】 PAGEREF _Tc11133 \h 8
\l "_Tc11136" 【题型6 由二次函数性质求二次函数的最值】 PAGEREF _Tc11136 \h 9
\l "_Tc31248" 【题型7 由二次函数的最值求字母的值】 PAGEREF _Tc31248 \h 10
\l "_Tc12038" 【题型8 由二次函数的最值求字母的取值范围】 PAGEREF _Tc12038 \h 12
【题型1 几何图形中线段最值问题】
【例1】（23-24九年级·广西钦州·期中）如图，线段AB=10，点P在线段AB上，在AB的同侧分别以AP,BP为边长作正方形APCD和BPEF，点M，N分别是EF，CD的中点，则MN的最小值是（ ）
A．2B．3C．5D．6
【变式1-1】（23-24九年级·安徽合肥·阶段练习）如图，AB=6，点C是AB上的动点，以AC、BC为边在AB同侧作等边三角形，M、N分别是CD、BE中点，MN最小值=（ ）
A．3B．32C．322D．332
【变式1-2】（23-24九年级·广东江门·阶段练习）如图，在矩形ABCD中，AB=3，BC=4，将对角线AC绕对角线交点O旋转，分别交边AD、BC于点E、F，点P是边DC上的一个动点，且保持DP=AE，连接PE、PF，设AE=x0(1)填空：PC= ，FC= ；（用含x的代数式表示）
(2)若△PEF的面积为S，求S与x的函数关系及△PEF面积的最小值；
(3)在运动过程中，PE⊥PF是否成立？若成立，求出x的值；若不成立，请说明理由．
【变式1-3】（23-24九年级·广东广州·期中）如图，在正方形ABCD中，AB=7，F是边CD上的动点，将△ADF绕点A顺时针旋转90°至△ABE，将△ADF沿AF翻折至△AGF，连接EF、BD交于点H，连接GH，则△EGH面积的最大值为 ．
【题型2 两线段和的最值问题】
【例2】（（23-24·安徽合肥·一模）如图，直线y=-x＋3与x轴、y轴分别交于B、C两点，抛物线y=-x2+bx+c经过点B、C，与x轴另一交点为A，顶点为D．
(1)求抛物线的解析式；
(2)在x轴上找一点E，使EC+ED的值最小，求EC+ED的最小值；
(3)在抛物线的对称轴上是否存在一点P，使得∠APB=∠OCB？若存在，求出P点坐标，若不存在，请说明理由．
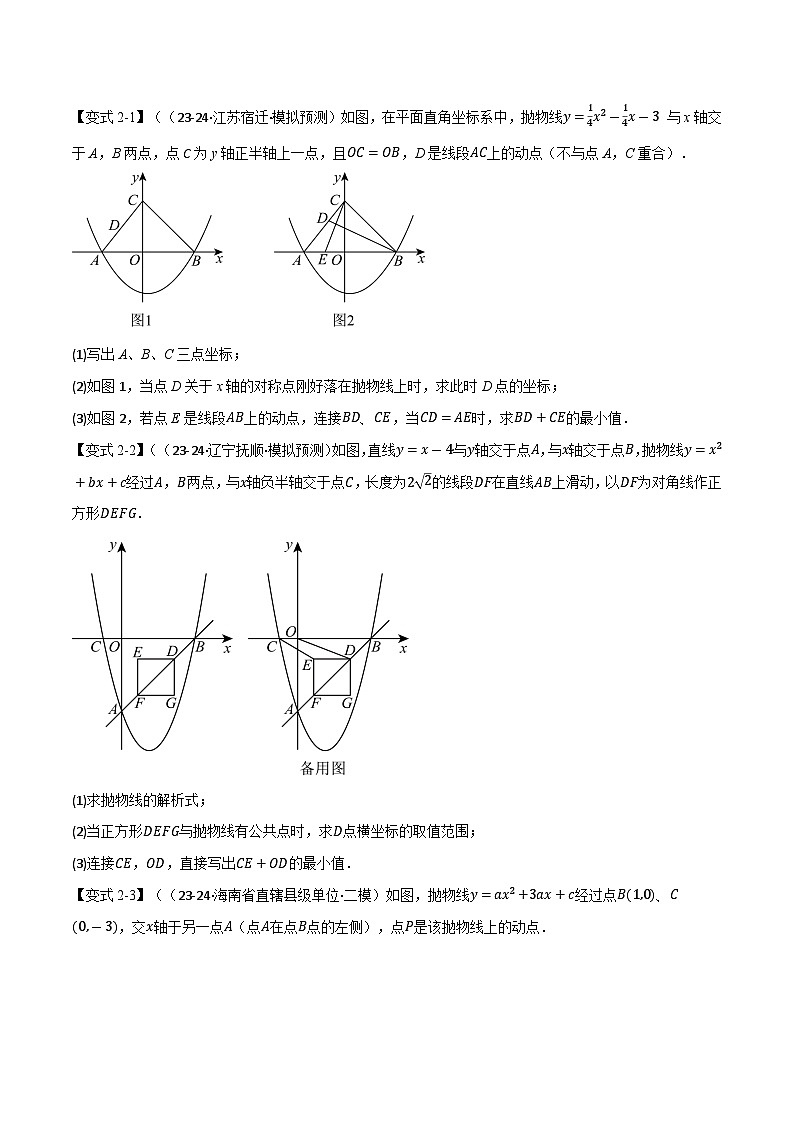
【变式2-1】（（23-24·江苏宿迁·模拟预测）如图，在平面直角坐标系中，抛物线y=14x2-14x-3 与x轴交于A，B两点，点C为y轴正半轴上一点，且OC=OB，D是线段AC上的动点（不与点A，C重合）．

(1)写出A、B、C三点坐标；
(2)如图1，当点D关于x轴的对称点刚好落在抛物线上时，求此时D点的坐标；
(3)如图2，若点E是线段AB上的动点，连接BD、CE，当CD=AE时，求BD+CE的最小值．
【变式2-2】（（23-24·辽宁抚顺·模拟预测）如图，直线y=x-4与y轴交于点A，与x轴交于点B，抛物线y=x2+bx+c经过A，B两点，与x轴负半轴交于点C，长度为22的线段DF在直线AB上滑动，以DF为对角线作正方形DEFG．
(1)求抛物线的解析式；
(2)当正方形DEFG与抛物线有公共点时，求D点横坐标的取值范围；
(3)连接CE，OD，直接写出CE+OD的最小值．
【变式2-3】（（23-24·海南省直辖县级单位·二模）如图，抛物线y=ax2+3ax+c经过点B1,0、C0,-3，交x轴于另一点A（点A在点B点的左侧），点P是该抛物线上的动点．
(1)求抛物线的解析式；
(2)当点P在直线AC下方且S△PAC=34S△AOC时，请求出点P的横坐标；
(3)在抛物线的对称轴l上是否存在点Q，使得QC+QB最小？若存在，请求出这个最小值；若不存在，请说明理由；
(4)若点E在x轴上，是否存在以P、A、C、E为顶点且以AC为一边的平行四边形？若存在，求点P的坐标；若不存在，请说明理由．
【题型3 周长的最值问题】
【例3】（（23-24·辽宁丹东·模拟预测）如图，对称轴为直线x=-1的抛物线y=a(x-h)2+ka≠0图象与x轴交于点A、B(点A在点B的左侧)，与y轴交于点C，其中点B的坐标为2,0，点C的坐标为0,4．
(1)求该抛物线的解析式；
(2)如图1，若点P为抛物线上第二象限内的一个动点，点M为线段CO上一动点，当△APC的面积最大时，求△APM周长的最小值；
(3)如图2，将原抛物线绕点A旋转180°，得新抛物线y'，在新抛物线y'的对称轴上是否存在点Q使得△ACQ为等腰三角形？若存在，请直接写出点Q的坐标；若不存在，说明理由．
【变式3-1】（23-24九年级·山东淄博·期中）如图，在平面直角坐标系中，抛物线y=-14x2+bx+c与x轴交于A-2，0，B6，0两点，与y轴交于点C，点P为直线BC上方抛物线上一动点．
(1)求抛物线的解析式；
(2)过点A作AD∥BC交抛物线于D，若点E为对称轴上一动点，求△BED周长的最小值及此时点E的坐标；
(3)过点A作AD∥BC交抛物线于D，过点E为直线AD上一动点，连接CP，CE，BP，BE，求四边形BPCE面积的最大值及此时点P的坐标．
【变式3-2】（23-24九年级·全国·期末）如图抛物线y=ax2+bx+c经过点A(-1,0)，点C(0,3)，且OB=OC．
(1)求抛物线的解析式及其对称轴；
(2)点D、E是直线x=1上的两个动点，且DE=1，点D在点E的上方，求四边形ACDE的周长的最小值；
(3)点P为抛物线上一点，连接CP，直线CP把四边形CBPA的面积分为3:5两部分，求点P的坐标．
【变式3-3】（23-24九年级·广东广州·阶段练习）如图，在平面直角坐标系中，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于点C，其中点A的坐标为-1,0，点C的坐标为0,-3．

(1)求抛物线的解析式；
(2)如图1，E为△ABC边AB上的一动点，F为BC边上的一动点，D点坐标为0,-2，
①求DE+EF的最小值②求△DEF周长的最小值；
(3)如图2，N为射线CB上的一点，M是地物线上的一点，M、N均在第一象限内，B、N位于直线AM的同侧，且AM∥CN，当△AMN为等腰三角形时，求点N的坐标．（直接写出点N的坐标，不要求写解答过程）
【题型4 面积的最值问题】
【例4】（23-24九年级·云南红河·期中）如图，抛物线y=ax2+bx-4与x轴交于A-3，0、B4，0两点，与y轴交于点C．
(1)求抛物线解析式；
(2)点H是抛物线对称轴上的一个动点，连接AH、CH，求出△ACH周长的最小值时点H的坐标；
(3)若点G是第四象限抛物线上的动点，求△BCG面积的最大值以及此时点G的坐标；
【变式4-1】（23-24九年级·甘肃武威·阶段练习）如图，抛物线y=ax2+bx+c与x轴交于点A-2,0和点B4,0，与y轴交于点C0,4．
(1)求抛物线的解析式．
(2)点D在抛物线的对称轴上，当AD+CD取得最小值时，求此时点D的坐标．
(3)点P是直线BC上方抛物线上一动点，连接CP、BP，求△PBC的面积的最大值，并求此时点P的坐标．
【变式4-2】（23-24九年级·山东·期末）如图所示，抛物线与x轴交于A、B两点，与y轴交于点C，且OA=1，OB=OC=4．

(1)求抛物线的解析式；
(2)若连接AC、BC．动点D从点A出发，在线段AB上以每秒1个单位长度向点B做匀速运动；同时，动点E从点B出发，在线段BC上以每秒2个单位长度向点C做匀速运动，当其中一点到达终点时，另一点随之停止运动，连接DE，设运动时间为t秒．在D、E运动的过程中，当t为何值时，四边形ADEC的面积最小，最小值为多少？
(3)点M是抛物线上位于x轴上方的一点，点N在x轴上，是否存在以点M为直角顶点的等腰直角三角形CMN？若存在，求出点M的坐标，若不存在，请说明理由．
【变式4-3】（23-24九年级·福建福州·期中）已知抛物线y=ax2+bx+ca≠0与y轴交于点A0,-5，顶点为B2,-1，过点C2,-5直线与抛物线交于D，E两点（点D在点E的左侧）．
(1)求抛物线的解析式；
(2)求△BDE面积的最小值；
(3)若D，E两点都在第四象限，过点D作直线y=-1的垂线，垂足为F，直线EB与直线DF交于点G，连接CF，求证：四边形BCFG是平行四边形．
【题型5 线段和差倍分的最值】
【例5】（23-24·山东济南·一模）抛物线y=-12x2+a-1x+2a与x轴交于Ab,0，B4,0两点，与y轴交于点C0,c，点P是抛物线在第一象限内的一个动点，且在对称轴右侧．
(1)求a，b，c的值；
(2)如图1，连接BC、AP，交点为M，连接PB，若S△PMBS△AMB=14，求点P的坐标；
(3)如图2，在（2）的条件下，过点P作x轴的垂线交x轴于点E，将线段OE绕点O逆时针旋转得到OE'，旋转角为α(0°<α<90°)，连接E'B，E'C，求E'B+34E'C的最小值．
【变式5-1】（23-24九年级·安徽合肥·阶段练习）如图，在平面直角坐标系中，抛物线y=-x2+23x的顶点为A点，且与x轴的正半轴交于点B．

（1）连接AO，AB，则△AOB为 三角形；
（2）P点为该抛物线对称轴上一点，当OP+12AP取最小值时，OP= ．
【变式5-2】（23-24九年级·安徽阜阳·阶段练习）已知抛物线与x轴相交于A，B两点，与y轴相交于点C0，6，顶点为D2，8．

(1)求此抛物线的解析式；
(2)如图1，点P为抛物线对称轴（直线l）上的动点，求当PB-PC取得最小值时点P的坐标；
(3)如图2，在第一象限内，抛物线上有一动点M，求△BCM面积的最大值．
【变式5-3】（23-24九年级·广东东莞·期中）如图，已知抛物线y=ax2+bx+c（a≠0）与y轴相交于点C0,-2，与x轴分别交于点B3,0和点A，且∠CAO=45°．
(1)求抛物线解析式；
(2)抛物线上是否存在一点Q，使得∠BAQ=∠ABC，若存在，请求出点Q坐标，若不存在，请说明理由；
(3)抛物线的对称轴交x轴于点D，在y轴上是否存在一个点P，使22PC+PD的值最小，若存在，请求出最小值，若不存在，请说明理由．
【题型6 由二次函数性质求二次函数的最值】
【例6】（23-24九年级·陕西西安·阶段练习）如图，抛物线y=ax2+bx+3与x轴交于点A1,0,B3,0，与y轴交于点C．

(1)求抛物线的解析式；
(2)点Mx1,y1,Nx2,y2是抛物线上不同的两点且x1+x2=4x1-x2，求y1-y2的最小值．
【变式6-1】（23-24九年级·江西赣州·期中）观察下列两个数的乘积，说明其中哪个积最大．
1×100,2×99,3×98,4×97,⋅⋅⋅,99×2,100×1．
【观察发现】（1）发现所列各组式子中两个因数的和都为_____________．
【问题解决】（2）若设其中一个因数为x（1≤x≤100，且为正整数），所列两个数的积为y，请说明哪个积最大，最大值是多少．
【拓展应用】（3）若大于0的a、b满足a+b=4，求a2+b2的最小值．
【变式6-2】（（23-24·贵州·模拟预测）已知二次函数y=ax2-4x+c（a≠0，a，c为常数）的图象经过点1,-6，-4,-1
(1)求二次函数的表达式；
(2)当-1≤x＜0时，求二次函数的最大值；
(3)当m≤x≤0时，二次函数的最大值与最小值的和为2m，求m的值．
【变式6-3】（23-24九年级·湖南长沙·开学考试）在平面直角坐标系中，我们将形如1,-1，-2.1,2.1这样，纵坐标与横坐标互为相反数的点称之为“互补点”．
(1)直线y=2x-3上的“互补点”的坐标为_________；
(2)直线y=kx+2k≠0上是否有“互补点”，若有，请求出点的坐标，若没有请说明理由；
(3)若函数y=14x2+n-k-1x+m+k-2的图象上存在唯一的一个“互补点”，且当-1≤n≤2时，m的最小值为k，求k的值．
【题型7 由二次函数的最值求字母的值】
【例7】（（23-24九年级·全国·专题练习）已知在平面直角坐标系中，设二次函数y1=x2+bx+a，y2=ax2+bx+1(a、b是实数，a≠0)．
(1)若函数y1的对称轴为直线x=3，且函数y1的图象经过点(a,-6)，求函数y1的表达式；
(2)若函数y1的图象经过点(r,0)，其中r≠0，求证：函数y2的图象经过点(1r，0)；
(3)设函数y1和函数y2的最小值分别为m和n，若m+n=0，求m、n的值．
【变式7-1】（23-24九年级·河南许昌·期末）如图，已知二次函数y=x2+ax+a-4的图象经过点P-2,-2．
(1)求a的值和二次函数图象的顶点坐标．
(2)已知点Qm,n在该二次函数图象上．
①当m=-3时，求n的值；
②当m≤x≤m+1时，该二次函数有最小值1，请结合函数图像求出m的值．
【变式7-2】（23-24九年级·湖南长沙·阶段练习）已知拋物线y=ax-h2+k与x轴交于A，B两点（A在B的左边），与y轴交于点C．顶点为M．

(1)如图，若该拋物线可以由抛物线y=ax2先向右平移5个单位，在向上平移4个单位得到，点C坐标为0,-21．
（i）求A，B两点的坐标；
（ii）若线段AM的垂直平分线交x轴交于点D，交y轴交于点E，交AM交于点P，求证：四边形ADME是菱形；
(2)已知a=1，抛物线顶点M在直线y=2x-5上，若在自变量x的值满足2h≤x≤2h+3的情况下，对应函数值y的最小值为14，求h的值．
【变式7-3】（（23-24·广西贺州·二模）如图，在平面直角坐标系中，已知抛物线y=ax2+bx-3与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，且OB=3OA=3．

(1)求这个二次函数的解析式；
(2)若点M是线段BC下方抛物线上的一个动点（不与点B，点C重合），过点M作直线MN⊥x轴于点D，交线段BC于点N．是否存在点M使得线段MN的长度最大，若存在，求线段MN长度的最大值，若不存在，请说明理由；
(3)当二次函数y=ax2+bx-3的自变量x满足t≤x≤t+1时，此函数的最大值与最小值的差为2，求出t的值．
【题型8 由二次函数的最值求字母的取值范围】
【例8】（23-24九年级·江苏南通·阶段练习）用好错题本可以有效的积累解题策略，减少再错的可能．下面是小颖同学错题本上的一道题，请仔细阅读，并完成相应任务．
任务一：请帮助小颖完成上述错题订正；
任务二：若点M2,y3也是此抛物线上的点，记抛物线在A，M之间的部分为图象G（包括M，A两点），记图形G上任意一点的纵坐标的最大值与最小值的差为t，若t≥y2-y1，直接写出m的取值范围．
【变式8-1】（23-24九年级·河南郑州·阶段练习）如图，已知二次函数y=-x2+bx+c的图象经过点A4,1，点B0,5．

(1)求该二次函数的表达式，并求出对称轴和顶点坐标；
(2)点Cm,n在该二次函数图象上，当m≤x≤4时，n的最大值为294，最小值为1，请根据图象直接写出m的取值范围．
【变式8-2】（（23-24·浙江温州·模拟预测）已知二次函数y=ax2-2ax+3图象的一部分如图所示，它经过-1,0．
(1)求这个二次函数的表达式，并在图中补全该图象；
(2)当-2≤x≤t时，函数的最大值为m，最小值为n，若m-n=9，求t的取值范围．
【变式8-3】（23-24九年级·湖北·周测）已知抛物线y=x2+bx+c经过点B，与y轴交于点A，顶点P在直线OB上．如图1，若点B的坐标为3,6，点P的横坐标为1．
(1)试确定抛物线的解析式；
(2)若当m≤x≤4时，y=x2+bx+c的最小值为2，最大值为11，请求出m的取值范围；
(3)已知：点M在抛物线上，点N的坐标为2,3，且∠MNA=∠BAN，请直接写出符合题意的点M的坐标．
*年*月*日 星期天
错题***
在平面直角坐标系中，抛物线y=x2-2mx+m2+1存在两点Am-1,y1，Bm+2,y2.
①求此抛物线的对称轴；（用含m的式子表示）
②记抛物线在A，B之间的部分为图象F（包括A，B两点），y轴上一动点C(0,a)，过点C作垂直于y轴的直线l与F有且仅有一个交点，求a的取值范围；