甘肃省武威第十七中学联片教研2024-2025学年上学期九年级数学第一次月考试卷

这是一份甘肃省武威第十七中学联片教研2024-2025学年上学期九年级数学第一次月考试卷，共10页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
一、单选题（共30分）
1．（3分）下列关于的方程中，一定是一元二次方程的为（ ）
A．B．
C．D．
2．（3分）明明在解关于x的方程时，抄错了a的符号，解出其中一个根是．则原方程的根的情况是（ ）
A．没有实数根B．有一个实数根是：
C．有两个相等的实数根D．有两个不相等的实数根
3．（3分）等腰三角形的两边的长是方程两个根，则此三角形的周长是（ ）
A．7B．8C．7或8D．以上都不对
4．（3分）用配方法解一元二次方程时，配方后的方程是（ ）
A．B．C．D．
5．（3分）若一个两位数等于它的十位数字与个位数字和的平方的三分之一，且个位数字比十位数字大5，则这个两位数是（ ）
A．27B．72C．27或16D．或
6．（3分）某网络学习平台2021年的新注册用户数为36万，2023年的新注册用户数为81万．设新注册用户数的年平均增长率为，则有（ ）
A．B．
C．D．
7．（3分）下列函数一定是二次函数的是（ ）
A．B．C．D．
8．（3分）若二次函数的图象经过点，则该图象必经过点（ ）
A．B．C．D．
9．（3分）在函数的图象上，当随的增大而减小时，的取值范围为（ ）
A．B．C．D．
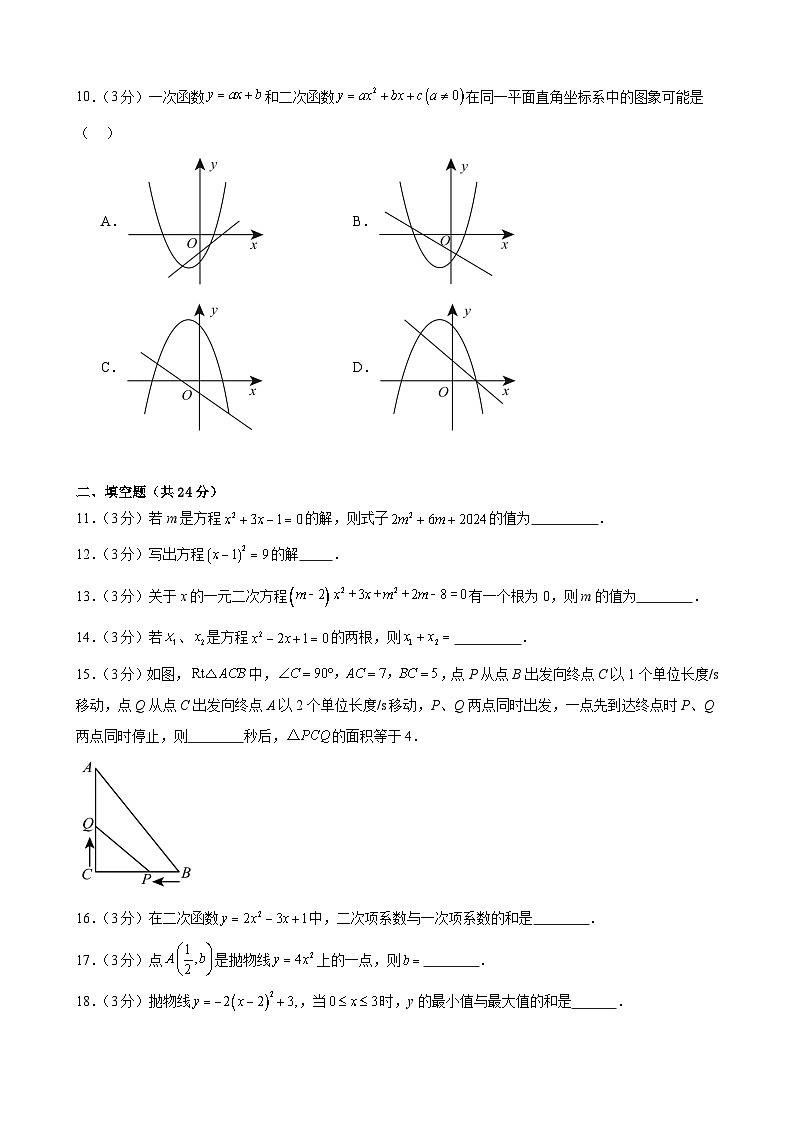
10．（3分）一次函数和二次函数在同一平面直角坐标系中的图象可能是（ ）
A．B．
C．D．
二、填空题（共24分）
11．（3分）若m是方程的解，则式子的值为 ．
12．（3分）写出方程的解 ．
13．（3分）关于x的一元二次方程有一个根为0，则m的值为 ．
14．（3分）若、是方程的两根，则 ．
15．（3分）如图，中，，点P从点B出发向终点C以1个单位长度/s移动，点Q从点C出发向终点A以2个单位长度/s移动，P、Q两点同时出发，一点先到达终点时P、Q两点同时停止，则 秒后，的面积等于4．
16．（3分）在二次函数中，二次项系数与一次项系数的和是 ．
17．（3分）点是抛物线上的一点，则 ．
18．（3分）抛物线，当时，y的最小值与最大值的和是 ．
三、解答题（共66分）
19．（12分）解下列方程．
(1)； (2)；
(3)； (4)．
20．（6分）已知二次函数．
(1)直接写出二次函数的对称轴和顶点坐标；
(2)在平面直角坐标系中，画出这个二次函数的简图；
(3)当随的增大而减小时，直接写出的取值范围．
21．（6分）已知．
(1)求，的值．
(2)若关于的一元二次方程有一个根是，求的值．
22．（6分）为了保障人民群众的生命安全和身体健康，某感冒退烧药生产企业产能逐步提升，10月份产量为256万片，11月、12月两个月增长率相同，预计12月份产量可达到400万片．求该企业感冒退烧药产量的月增长率．
23．（6分）已知关于x的方程．
(1)求证：不论a取任何实数，该方程都有两个不相等的实数根．
(2)若方程有一个根为，求a的值及该方程的另一个根；
24．（6分）已知函数 （为常数）．
(1)求当为何值时是的二次函数？
(2)在（）的条件下，点在此函数图象上，求的值．
25．（6分）如图，已知点在抛物线上，过点A且平行于x轴的直线交抛物线于点B．
(1)求a的值和点B的坐标；
(2)若点P是抛物线上一点，当以点A，B，P为顶点构成的的面积为2时，求点P的坐标．
26．（8分）如图，点C为二次函数的顶点，直线与该二次函数图象交于、B两点（点B在y轴上），与二次函数图象的对称轴交于点D．
(1)求m的值及点C坐标；
(2)在该二次函数的对称轴上是否存在点Q，使得以A，C，Q为顶点的三角形是等腰三角形？若存在，请求出符合条件的Q点的坐标；若不存在，请说明理由．
27．（10分）如图，已知抛物线交x轴于点，，交y轴于点C．
(1)求抛物线的解析式：
(2)若D为直线上方的抛物线上的一点，且的面积为3，求点D的坐标；
(3)将抛物线向右平移个单位长度，设平移后的抛物线中y随x增大而增大的部分记为图象G， 若图象G与直线只有一个交点，求m的取值范围．
答案
11． 12．， 13． 14．2 15．1
16． 17． 18．
19．(1)
(2)
(3)，
(4)，
20．（1）解：的对称轴为直线，顶点坐标为2,-1；
（2）解：列表：
描点画图，得：
（3）解：由抛物线开口向上，对称轴为直线，
则当随的增大而减小时，的取值范围为．
21．（1），
根据二次根式非负性可得且，
解之：，
，
，．
（2）依（1）得：该一元二次方程为，
关于的一元二次方程有一个根是，
，
解之：，
的值为．
22．设该企业感冒退烧药产量的月增长率为，由题意，得：
，
解得：或（舍去）；
答：设该企业感冒退烧药产量的月增长率为．
23．（1）证明：，
∵，
∴，
∴不论a取任何实数，该方程都有两个不相等的实数根；
（2）解：根据题意，将代入方程中，得，
解得，
∴方程为，即，
解得，，
即a的值为，该方程的另一个根为3．
24．（1）解：由题意得，且，
解得，
∴当时是的二次函数；
（2）解：∵，
∴，
∵点在此函数图象上，
∴．
25．（1）解：把代入中得：，
∴，
∴抛物线解析式为，
∴抛物线的对称轴为y轴，
∵轴，且点B在抛物线上，
∴点A和点B关于抛物线对称轴对称，即关于y轴对称，
∴
（2）解：∵，，
∴，
∵的面积为2，轴，
∴，
∴，
∴或，
在中，当时，，当时，，
∴点P的坐标为或或或．
26．（1）解： 直线过点，
，
，
，
，
二次函数解析式为，
顶点坐标为；
（2）解：存在点，使得以，，为顶点的三角形是等腰三角形．
顶点坐标为，
对称轴为直线，
过点作于点，
在中，．
①当时，设，
在中，
解之得
；
②当时，根据等腰三角形三线合一得：，
，
；
③当时，，
，．
综上所述：点的坐标为或或或．
27．（1）解：将，代入得：
，
解得：，
∴抛物线解析式为；
（2）解：当时，，
∴，
设直线的解析式为，
把，代入得：
，
解得：，
∴直线的解析式为，
过点D作y轴的平行线，交于点E，
设，则，
∴，
∴，
解得：，
∴或；
（3）解：①当平移后的抛物线顶点在直线左侧时：
∵，，
∴抛物线的对称轴为直线，
∴抛物线顶点坐标为，
∴平移后的抛物线的顶点坐标为，
把代入得：，
解得：，
∵图象G与直线只有一个交点，
∴；
②当平移后的抛物线与直线相切时：
∵抛物线解析式为，
∴平移后的解析式为，
∵图象G与直线只有一个交点，
∴方程方程有两个相同实根，
整理为，
∴，
解得：，
综上：或．
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
C
B
A
D
B
B
A
C