2025中考复习数学考点专题探究课件：专题5　一次函数、反比例函数与几何综合

这是一份2025中考复习数学考点专题探究课件：专题5　一次函数、反比例函数与几何综合，共29页。PPT课件主要包含了专题5，刷难关等内容，欢迎下载使用。
专题5　一次函数、反比例函数与几何综合
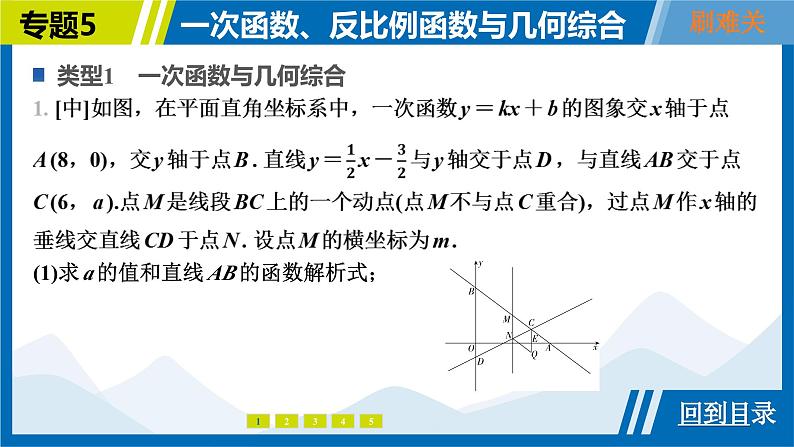
类型1　一次函数与几何综合
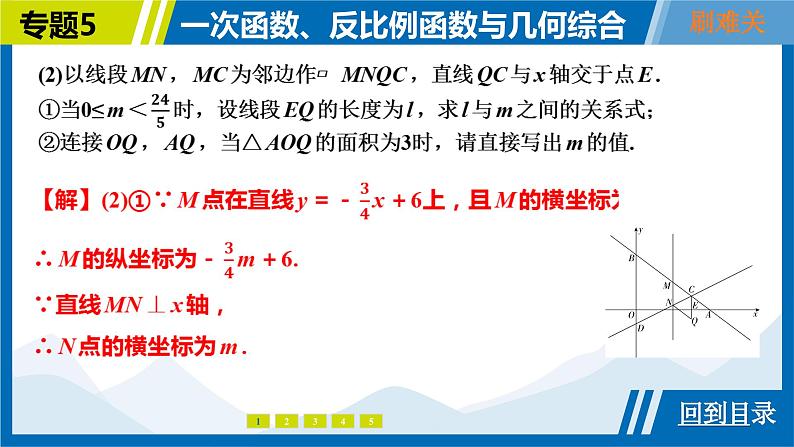
(1)求a的值和直线AB的函数解析式；
2. [2023甘肃兰州中考，较难]在平面直角坐标系中，给出如下定义： P为图形M上任意一点，如果点P到直线EF的距离等于图形M上任意两点距 离的最大值时，那么点P称为直线EF的“伴随点”.例如：如图(1)，已知点 A(1，2)，B(3，2)，P(2，2)在线段AB上，则点P是直线EF：x轴的“伴随 点”.

(3)如图(4)，以A(1，0)，B(2，0)，C(2，1)为顶点的正方形ABCD上始终存 在点P，使得点P是直线EF：y＝－x＋b的“伴随点”，请直接写出b的取 值范围.
当b≤1时，l1为y＝－x＋b＋2，当l1过A时，b＝－1，当l1过C时，b＝1，即－1≤b≤1；当b＞1时，l1为y＝－x＋b－2，当l1过A时，b＝3，当l1过C时，b＝5，即3≤b≤5.
综上所述，当－1≤b≤1或3≤b≤5时，正方形ABCD上始终存在点P，使 得点P是直线EF：y＝－x＋b的“伴随点”.
类型2　反比例函数与几何综合
(1)m＝ 　　　　　，k＝ 　　　　　，点C的坐标为 　　　　　；
【解】(1)当x＝1时，y＝－3x＝－3＝m，即点B(1，－3).
将点B的坐标代入反比例函数的解析式得k＝－3×1＝－3，
如图，过点A作AH⊥x轴于点H，
∴OH＝1，AH＝3.
又∵∠ACH＝45°，∠AHC＝90°，
∴∠ACH＝∠CAH＝45°，
∴AH＝CH＝3，则CO＝CH＋OH＝4，
∴点C的坐标为(－4，0)，故答案为－3，－3，(－4，0).
(2)点P在x轴上，若以B，O，P为顶点的三角形与△AOC相似，求点P的坐标.
(1)求k，m的值；
(2)平行于y轴的动直线与l和反比例函数的图象分别交于点D，E，若以B， D，E，O为顶点的四边形为平行四边形，求点D的坐标.

(1)求反比例函数的解析式.
【解】(1)∵点B坐标为(6，12)，∴CB＝12.
∵BE＝2CE，∴CE＝4，∴E(6，4).
(2)点P是第一象限内位于反比例函数图象上的一个动点，作点P关于原点对 称的点P'，以PP'为斜边作等腰直角三角形MPP'，点M在第四象限.①如图(2)，当点P与点E重合时，求点M的坐标；②在同一平面内，若等腰直角三角形的一边所在的直线与一条直线垂直，则 称此等腰直角三角形为这条直线的“关联三角形”.在点P的运动过程中等腰 直角三角形MPP'是否能成为直线DE的“关联三角形”？若能，请求出此时 点P坐标；若不能，请说明理由.
【解】(2)①如图(1)，过点E作EG⊥x轴，过点M作HG∥x轴，交EG于点G，过点P'作P'H⊥HG于点H. ∵∠EMP'＝90°，∴∠P'MH＋ ∠EMG＝90°.∵∠P'MH＋∠MP'H＝90°，∴∠EMG＝∠MP'H. ∵EM＝P'M，∠G＝∠H＝90°，∴△EGM≌△MHP'(AAS)，∴HM＝EG，P'H＝MG. 设M(x，y).∵E(6，4)，∴P'(－6，－4)，∴－4－y＝6－x，x＋6＝4－y，解得x＝4，y＝－6，