高考数学一轮复习课时质量作业(十二)含答案

这是一份高考数学一轮复习课时质量作业(十二)含答案，共7页。试卷主要包含了对实数a和b，定义运算“◎”等内容，欢迎下载使用。

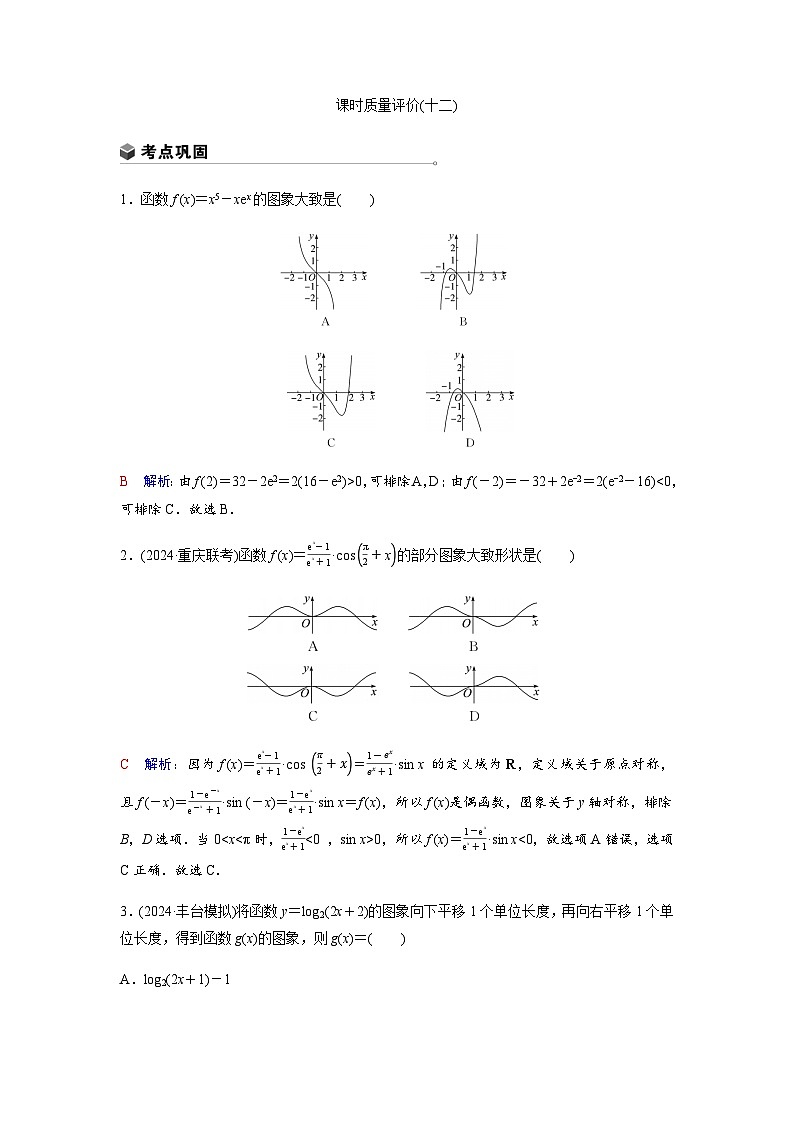
1．函数f (x)＝x5－xex的图象大致是( )
B 解析：由f (2)＝32－2e2＝2(16－e2)>0，可排除A，D；由f (－2)＝－32＋2e-2＝2(e-2－16)<0，可排除C．故选B．
2．(2024·重庆联考)函数f (x)＝ex－1ex+1·csπ2+x的部分图象大致形状是( )
C 解析：因为f (x)＝ex－1ex+1·cs π2+x＝1-exex+1·sin x 的定义域为R，定义域关于原点对称，且f (－x)＝1－e－xe－x +1·sin (－x)＝1－exex+1·sin x＝f (x)，所以f (x)是偶函数，图象关于y轴对称，排除B，D选项．当00，所以f (x)＝1－exex+1·sin x<0，故选项A错误，选项C正确．故选C．
3．(2024·丰台模拟)将函数y＝lg2(2x＋2)的图象向下平移1个单位长度，再向右平移1个单位长度，得到函数g(x)的图象，则g(x)＝( )
A．lg2(2x＋1)－1
B．lg2(2x＋1)＋1
C．lg2x－1
D．lg2x
D 解析：将函数y＝lg2(2x＋2)的图象向下平移1个单位长度，再向右平移1个单位长度，可得g(x)＝lg2[2(x－1)＋2]－1＝lg2(2x)－1＝lg2x的图象．
4．(多选题)已知函数f (x)＝－xx+1，则函数具有下列性质( )
A．函数f (x)在定义域内是减函数
B．函数f (x)的值域为(－∞，－1)∪(－1，＋∞)
C．函数f (x)的图象关于直线x＝－1对称
D．函数f (x)的图象关于点(－1，－1)对称
BD 解析：因为f (x)＝－xx+1＝－x+1－1x+1＝－1+1x+1，所以该函数图象由y＝1x的图象向左平移1个单位长度，再向下平移1个单位长度得到，如图所示．
由图可知，函数f (x)在(－∞，－1)和(－1，＋∞)上单调递减，所以选项A错误；函数f (x)的值域为(－∞，－1)∪(－1，＋∞)，所以选项B正确；函数f (x)的图象关于点(－1，－1)对称，所以选项C错误，选项D正确．故选BD．
5．已知定义在R上的偶函数f (x)，在(－∞，0]上单调递减，且f (3)＝0，则不等式(x＋3)f (x)<0的解集是( )
A．{x|x＜－3或x＞3}
B．{x|x＜－3或0＜x＜3}
C．{x|－3＜x＜3且x≠0}
D．{x|x＜3且x≠－3}
D 解析：由题意，画出f (x)的示意图如图所示．
(x＋3)f (x)<0等价于x+3<0，f x >0或x+3>0，f x <0，结合图可得解集为xx＜3且x≠－3}.故选D．
6．如图所示可能是下列哪个函数的图象( )
A．y＝2x－x2－1B．y＝2xsinx4x+1
C．y＝(x2－2x)exD．y＝xlnx
C 解析：函数的定义域为R，排除D；对于A，当x＝－1时，y＝2-1－1－1＝－32＜0，排除A；对于B，当sin x＝0时，y＝0，所以y＝2x·sinx4x+1有无数个零点，排除B．故选C．
7．函数y＝1x－1的图象与函数y＝2|sin πx|(－2≤x≤4)的图象所有交点的横坐标之和等于( )
A．8B．10
C．12D．14
C 解析：函数y＝1x－1与y＝2|sin πx|的图象有公共对称轴x＝1，分别作出这两个函数的图象如图所示．
由图象可知，两个函数共有12个交点，且关于直线x＝1对称，则所有交点的横坐标之和为6×2＝12.故选C．
8．在同一平面直角坐标系中，若函数y＝2a与y＝|x－a|－1的图象只有一个交点，则a的值为________.
－12 解析：在同一平面直角坐标系中，作出函数y＝2a与y＝|x－a|－1的大致图象，如图所示．由题意，可知2a＝－1，则a＝－12.
9．(2024·松原模拟)对a，b∈R，记max{a，b}＝a，a≥b，b，a＜b，函数f (x)＝max{|x＋1|，|x－2|}(x∈R)的最小值是________.
32 解析：函数f(x)＝max{|x＋1|，|x－2|}(x∈R)的图象如图所示，由图象可得，其最小值为32．
10．(新定义)对实数a和b，定义运算“◎”：a◎b＝a，a－b≤1，b，a－b>1，设函数f (x)＝(x2－2)◎(x－x2)，x∈R.若函数y＝f (x)－c的图象与x轴恰有3个公共点，则实数c的取值范围是( )
A．(－2，－1]
B．－∞，－2∪－1，－34
C．－34，+∞
D．(－1，＋∞)
A 解析：因为f (x)＝(x2－2)◎(x－x2)，x∈R，所以当x2－2－(x－x2)≤1，即－1≤x≤32时，f (x)＝x2－2；当x2－2－(x－x2)>1，即x<－1或x>32时，f (x)＝x－x2，作出f (x)的图象，如图所示．
函数y＝f (x)－c的图象与x轴恰有3个公共点，转化为函数y＝f (x)与y＝c恰有三个交点，由图象可得－211．已知函数f (x)＝2x2+4x+1，x<0，2ex，x≥0， 则y＝f (x)(x∈R)的图象上关于坐标原点O对称的点共有( )
A．0对B．1对
C．2对D．3对
C 解析：作出函数f (x)＝2x2+4x+1，x<0，2ex，x≥0， 的图象，如图所示，
则y＝f (x)(x∈R)的图象上关于坐标原点对称的点，即当x<0时，f (x)＝2x2＋4x＋1的图象关于原点对称产生的新曲线与y＝2ex的图象的交点．
由图象可知，函数f (x)＝2x2+4x+1，x<0，2ex，x≥0， 的图象上关于坐标原点对称的点共有2对．故选C．
12．如图，函数y＝f (x)的图象是圆x2＋y2＝2上的两段弧，则不等式f (x)>f (－x)－2x的解集是________.
{x|－1＜x＜0，或1＜x＜2} 解析：由图象可知函数f (x)为奇函数，故f (x)>f (－x)－2x⇔f (x)－f (－x)>－2x⇔2f (x)>－2x，即f (x)>－x.联立x2+y2＝2，y＝－x，解得x＝－1，y＝1或x＝1，y＝－1，在同一平面直角坐标系中分别作出y＝f (x)与y＝－x的图象，如图所示．
由图象可知，不等式的解集为{x|－1＜x＜0，或1＜x＜2}．
13．已知函数f (x)＝lnx，x＞0，gx，x＜0，若∃x0∈(－∞，0)，使得f (x0)＋f (－x0)＝0成立，请写出一个符合条件的函数g(x)的表达式________.
g(x)＝1x(答案不唯一) 解析：由∃x0∈(－∞，0)，使得f(x0)＋f(－x0)＝0，可得g(x0)＝－f(－x0)．由y＝f(x)与y＝－f(－x)图象关于原点对称，可得y＝ln x与y＝－ln (－x)图象关于原点对称，如图所示．
取y＝1x时，在第三象限显然有一交点x0，故取g(x)＝1x符合题意．
14．(2024·乐山模拟)设函数f (x)的定义域为R，满足f (x＋1)＝2f (x)，且当x∈(0，1]时，f (x)＝x(1－x)．若对任意x∈(－∞，m]，都有f (x)≤38，则m的取值范围是______.
－∞，54 解析：因为f (x＋1)＝2f (x)，所以f (x)＝2f (x－1)．又当x∈(0，1]时，f (x)＝－x-122＋14∈0，14，所以当x∈(1，2]时，x－1∈(0，1]，f(x)＝2f(x－1)＝2(x－1)(2－x)＝－2x-322＋12∈0，12．当x∈(1，2]时，由f(x)＝38，得x＝54或74．又当x∈(－1，0]时，x＋1∈(0，1]，f(x)＝12f(x＋1)＝－12x(x＋1)＝－12x+122＋18∈0，18，因此易知当x≤0时，f (x)≤18<38，f (x)在(－1，2]上的图象如图所示．
由图可知m的取值范围是－∞，54.