
01 第40讲 空间几何体 【正文】听课 高考数学二轮复习练习
展开
这是一份01 第40讲 空间几何体 【正文】听课 高考数学二轮复习练习,共9页。试卷主要包含了空间几何体的表面积与体积公式等内容,欢迎下载使用。
1.利用实物、计算机软件等观察空间图形,认识柱、锥、台、球及简单组合体的结构特征,能运用这些特征描述现实生活中简单物体的结构.
2.知道球、柱、锥、台的表面积和体积的计算公式,能用公式解决简单的实际问题.
3.能用斜二测画法画出简单空间图形(长方体、球、圆柱、圆锥、棱柱及其简单组合)的直观图.
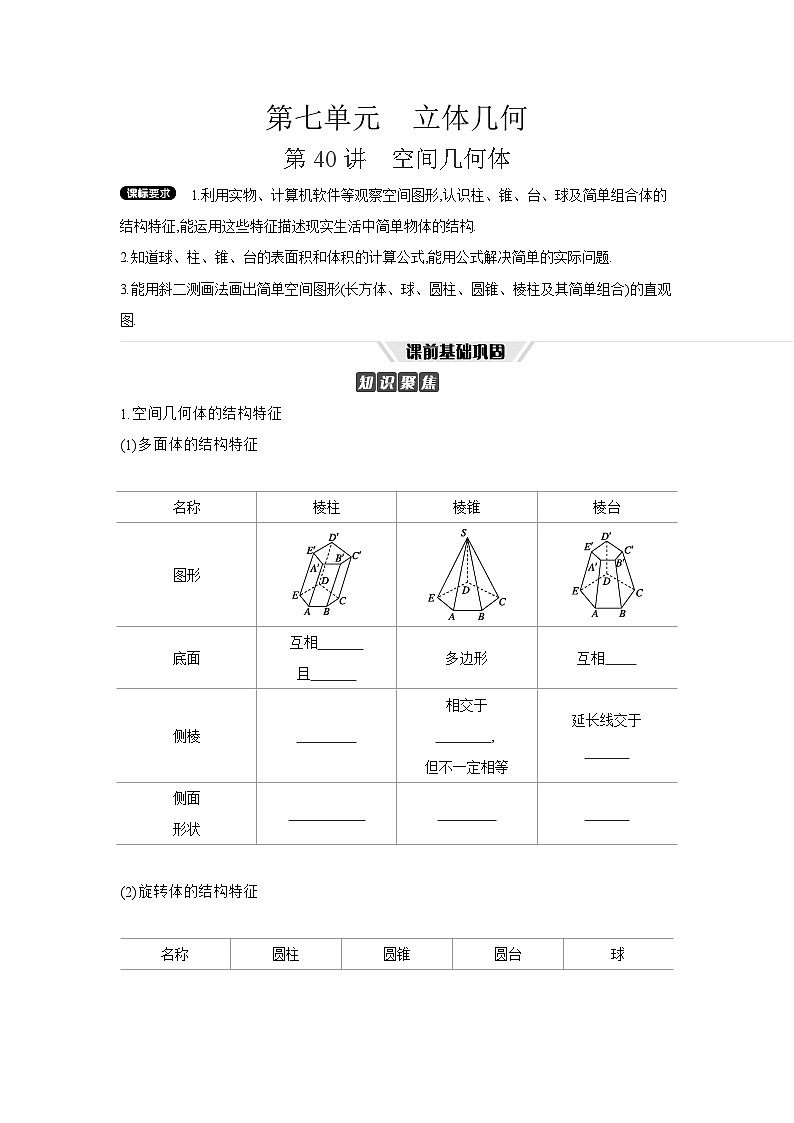
1.空间几何体的结构特征
(1)多面体的结构特征
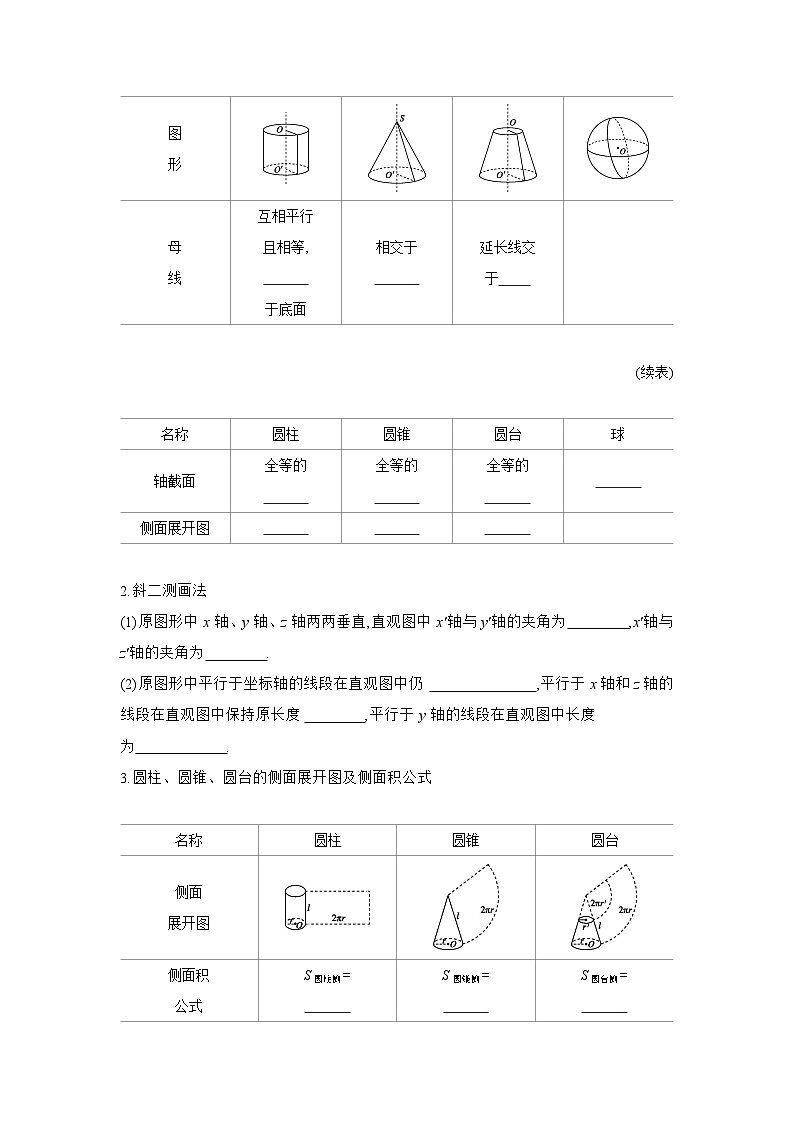
(2)旋转体的结构特征
(续表)
2.斜二测画法
(1)原图形中x轴、y轴、z轴两两垂直,直观图中x'轴与y'轴的夹角为 ,x'轴与z'轴的夹角为 .
(2)原图形中平行于坐标轴的线段在直观图中仍 ,平行于x轴和z轴的线段在直观图中保持原长度 ,平行于y轴的线段在直观图中长度为 .
3.圆柱、圆锥、圆台的侧面展开图及侧面积公式
4.空间几何体的表面积与体积公式
(其中柱体、锥体、台体的高为h,球的半径为R)
常用结论
1.按照斜二测画法得到的平面图形的直观图,其面积与原图形面积的关系如下:
S直观图=24S原图形,S原图形=22S直观图.
2.球的截面的性质
(1)球的任何截面都是圆面;
(2)球心和截面(不过球心)圆心的连线垂直于截面;
(3)球心到截面的距离d与球的半径R及截面的半径r的关系为r=R2-d2.
3.多面体的内切球与外接球常用的结论:
(1)设正方体的棱长为a,则它的内切球半径r=a2,外接球半径R=32a;
(2)设长方体的长、宽、高分别为a,b,c,则它的外接球半径R=a2+b2+c22;
(3)设正四面体的棱长为a,则它的高为63a,内切球半径r=612a,外接球半径R=3r=64a.
题组一 常识题
1.[教材改编] 下列说法中错误的是 .
①经过不共面的四点的球有且仅有一个;②平行六面体的每个面都是平行四边形;③正棱柱的每条侧棱均与上下底面垂直;④棱台的每条侧棱均与上下底面不垂直.
2.[教材改编] 如图,一个水平放置的三角形ABO用斜二测画法画出的直观图是等腰直角三角形A'B'O',若B'A'=B'O'=1,那么原三角形ABO的周长是 .
3.[教材改编] 长、宽、高分别为1,2,3的长方体的顶点都在同一球面上,则该球的表面积为 .
题组二 常错题
◆索引:对空间几何体的相关公式掌握不牢致误;对空间几何体的结构特征认识不到位致误;几何体形状不确定时,不会分类讨论致误.
4.一个圆锥的侧面展开图是圆心角为4π3,半径为18的扇形,则圆锥的高为 .
5.如图所示,将一个长方体用过同一顶点的三条棱中点的平面截出一个棱锥,则该棱锥的体积与剩下的几何体体积的比为 .
6.圆柱的侧面展开图是边长为6π和4π的矩形,则圆柱的体积是 .
基本立体图形与直观图
角度1 直观图
例1 用斜二测画法画出的一个水平放置的平面图形的直观图为如图所示的直角梯形,其中B'C'=A'B'=1,A'B'∥C'D',B'C'⊥C'D',则原平面图形的面积为( )
A.328B.324C.32D.62
总结反思
用斜二测画法画几何体的直观图,掌握线段位置、长度两要素的变化规律即可.几何体的直观图和原几何体的关系(形状和数量关系)是解题重点.
变式题 (1)已知正三角形ABC的边长为2,那么用斜二测画法作出的△ABC的直观图△A'B'C'的面积为( )
A.3B.32
C.62D.64
(2)(多选题)在水平放置的三角形ABC的直观图A'B'C'中,D'是△A'B'C'的边B'C'上的一点,且D'C'
相关试卷
这是一份01 第55讲 随机抽样 【正文】听课 高考数学二轮复习练习,共7页。试卷主要包含了知道获取数据的基本途径,包括等内容,欢迎下载使用。
这是一份01 第40讲 空间几何体 【答案】听课 高考数学二轮复习练习,共6页。
这是一份01 第40讲 空间几何体 【正文】作业 高考数学二轮复习练习,共6页。









