




还剩36页未读,
继续阅读
所属成套资源:全套青岛版七年级数学上册课时课件
成套系列资料,整套一键下载
青岛版七年级数学上册第6章基本的几何图形素养综合检测课件
展开
这是一份青岛版七年级数学上册第6章基本的几何图形素养综合检测课件,共44页。
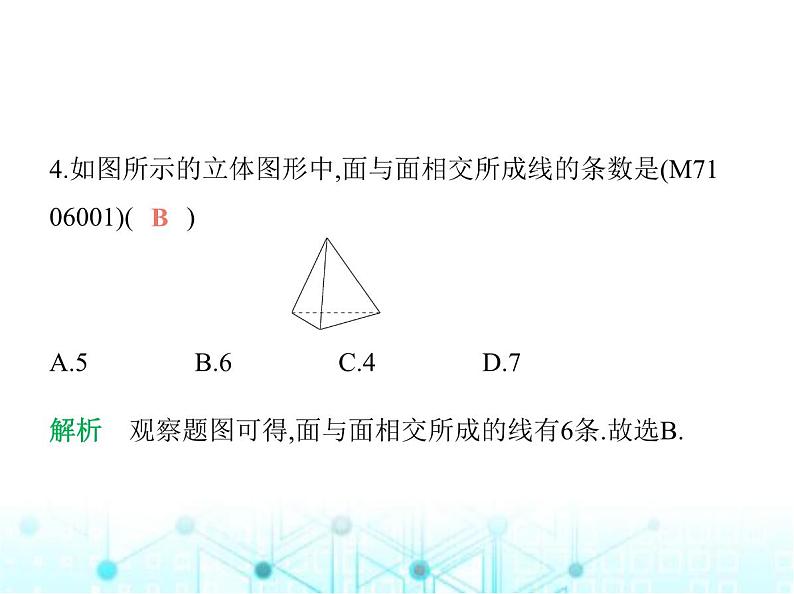
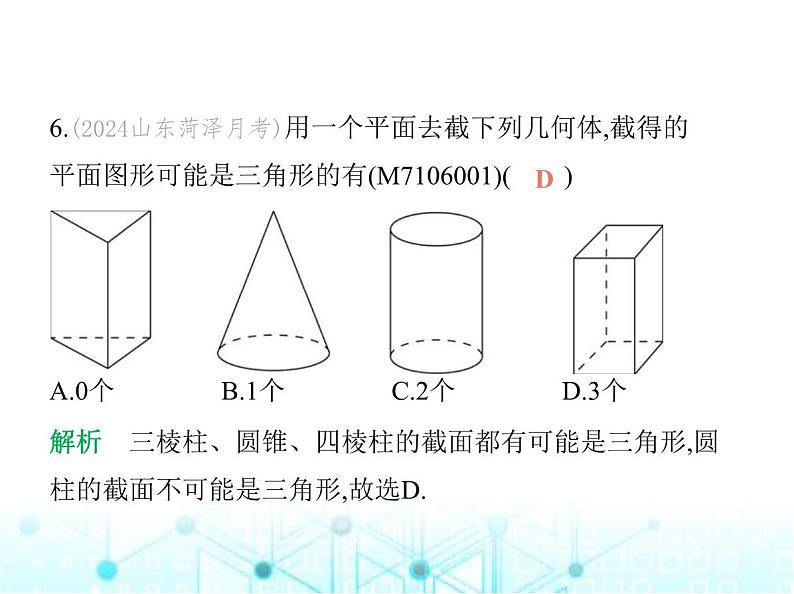
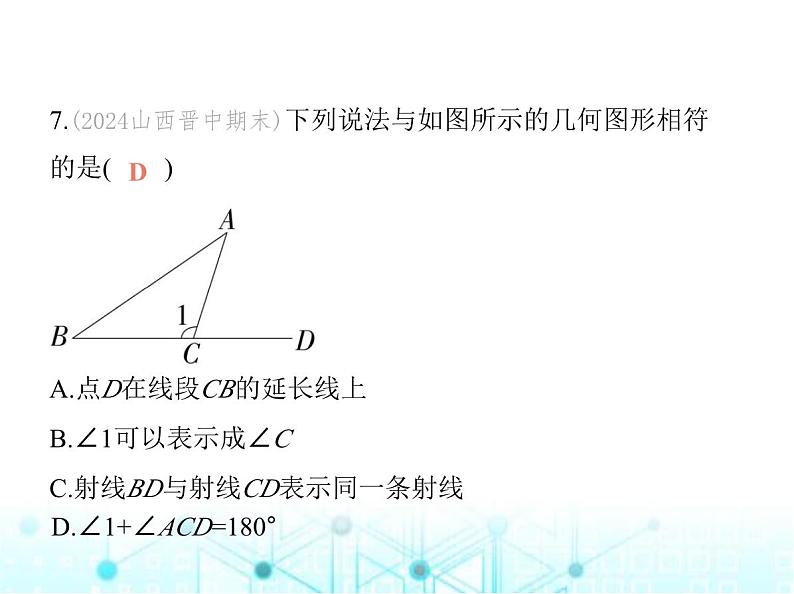
第6章 素养综合检测(满分100分, 限时60分钟)一、选择题(每小题3分,共36分)1.(2024山东济南济阳期中)下列四个几何体中,是棱柱的是 (M7106001)( )A. B. C. D. B解析 选项A中的几何体是圆柱;选项B中的几何体是三棱 柱;选项C中的几何体是三棱锥;选项D中的几何体是四棱台. 故选B.2.(2024山东烟台牟平期中)如图,把图形绕着给定的直线旋 转一周后形成的几何体是(M7106001)( ) A. B. C. D. D3.下面的几何体中,全是由曲的面围成的是(M7106001)( )A.圆柱 B.圆锥 C.球 D.正方体C解析 A.圆柱是由两个平的面和一个曲的面围成的;B.圆锥 是由一个曲的面和一个平的面围成的;C.球是由一个曲的面 围成的;D.正方体是由六个平的面围成的.故选C.4.如图所示的立体图形中,面与面相交所成线的条数是(M71 06001)( ) A.5 B.6 C.4 D.7 B解析 观察题图可得,面与面相交所成的线有6条.故选B.5.(跨学科·语文)(2022河北保定唐县期末)《红楼梦》中有这 么一句话,“自古道:‘千里姻缘一线牵’,管姻缘的有一位 月下老人,预先注定,暗里只用一根红线,把这两个人的脚绊 住.”若这里所说的“线”是真的,则在数学中指的应是( )A.直线 B.射线C.线段 D.以上都不对C解析 由题意可知,两个人可以看作两个点,所以若这里所说 的“线”是真的,则在数学中指的应是线段.故选C.6.(2024山东菏泽月考)用一个平面去截下列几何体,截得的 平面图形可能是三角形的有(M7106001)( ) A.0个 B.1个 C.2个 D.3个D解析 三棱柱、圆锥、四棱柱的截面都有可能是三角形,圆 柱的截面不可能是三角形,故选D.7.(2024山西晋中期末)下列说法与如图所示的几何图形相符 的是( ) A.点D在线段CB的延长线上B.∠1可以表示成∠CC.射线BD与射线CD表示同一条射线D.∠1+∠ACD=180° D解析 A.点D在线段BC的延长线上,所以A中说法错误;B.∠1 不可以表示成∠C,所以B中说法错误;C.射线BD与射线CD是 两条射线,所以C中说法错误;D.∠1+∠ACD=180°,所以D中 说法正确.故选D.8.点P在直线a上,也在直线b上,但不在直线c上,且直线a、b、 c两两相交,下列符合上述条件的图形是 ( ) A B C D D解析 观察选项中的图形可知只有D选项符合题意,故选D.9.射线OA上有B、C两点,若OB=8,BC=2,线段OB、BC的中点 分别为D、E,则线段DE的长为 ( )A.5 B.1或3 C.1 D.5或3 D解析 因为OB=8,D是OB的中点,所以DB=4,因为BC=2,E是BC的中点,所以BE=1.如图1,DE=BD-BE=3;如图2,DE=BD+BE=5.所以DE的长为5或3.故选D. 图1 图2 10.(情境题·中华优秀传统文化)曲桥是我国古代经典建筑之 一,它的修建增加了游人在桥上行走的路程,有利于游人更好 地观赏风光.两地间修建曲桥与修建直的桥相比,增加了桥的 长度,蕴含的数学道理是(M7101003)( )A.两点之间,线段最短B.两点确定一条直线C.经过一点可以作无数条直线D.连接两点间线段的长度叫作两点间的距离A解析 根据线段的性质可知,两地间修建曲桥与修建直的桥 相比,增加了桥的长度,蕴含的数学道理是两点之间,线段最 短,故选A.11.(2024山东潍坊潍城期中)小亮正确完成了以下两道作图 题:①延长线段AB到C,使BC=AB.②反向延长线段DE到F,使 点D是线段EF的一个三等分点.针对小亮的作图,小莹说: “点B是线段AC的中点.”小轩说:“DE=2DF.”下列说法正 确的是( )A.小莹、小轩都对B.小莹不对,小轩对C.小莹、小轩都不对D.小莹对,小轩不对D解析 延长线段AB到C,使BC=AB,如图①所示,此时点B是线 段AC的中点.反向延长线段DE到F,使点D是线段EF的一个 三等分点,如图②所示,有两种情况,有DE=2DF或DE= DF.因此小莹说得对,小轩说得不对.故选D. 图① 图②12.如图,已知∠AOB=180°,∠AOC=110°,现将射线OA绕点O 顺时针匀速旋转,射线OB保持不动,当射线OA与射线OB重合 时停止旋转.当三条射线构成的角中有两个角相等(重合除 外)时,射线OA旋转的角度为 ( ) A.40° B.60°C.40°或145° D.60°或150°C解析 经分析,三条射线构成的角中有两个角相等(重合除 外)时,存在以下两种情形:①当射线OA旋转到∠BOC的外部 时,∠AOC=∠BOC=70°,此时射线OA旋转的角度为110°-70°=40°.②当射线OA旋转到∠BOC的内部时,∠AOC=∠AOB,此 时∠AOB= ∠BOC=35°,射线OA旋转的角度为180°-35°=145°.综上,射线OA旋转的角度为40°或145°.故选C.二、填空题(每小题3分,共18分)13.(2022山东济南期末)计算:30°12'= °.30.2解析 因为1°=60',所以12'=0.2°,所以30°12'=30.2°.14.如图①,A点为公交车车站,点B、C、D为三家在同一条直 线上的医院,E点为医护人员住宿楼,公交车完成接送任务需 返回车站,则在送医护人员回住宿楼的过程中,最近的路线为 A→B→C→D→E→A(如图②),其根据是 . 两点之间,线段最短解析 在送医护人员回住宿楼的过程中,最近的路线为A→B →C→D→E→A,其依据是两点之间,线段最短.15.(2024山东德州平原期末)如图,点O在直线AB上,射线OF 平分∠AOD,∠EOF=∠AOC=90°,在图中与∠AOF互余的角 一共有 个.(M7106006) 3解析 ∵射线OF平分∠AOD,∴∠AOF=∠DOF,∵∠EOF=∠AOC=90°,∴∠AOF+∠COF=∠AOC=90°,∠AOF+∠BOE=180°-∠EOF =90°,∠DOF+∠DOE=∠EOF=90°,∴与∠AOF互余的角有∠COF,∠BOE,∠DOE,共3个,故答案 为3.16.(2024山东聊城东昌府期中)线段AB上有P、Q两点,AB=26,AP=14,PQ=11,那么BQ= . 23或1解析 本题有两种情形:①当点Q在线段AP上时,如图,BQ=BP+PQ=AB-AP+PQ=26-14+11=23; ②当点Q在线段BP上时,如图,BQ=BP-PQ=AB-AP-PQ=26-14- 11=1. 故答案为23或1.17.如图,点A、B、C在同一直线上,H为AC的中点,M为AB的 中点,N为BC的中点,则下列说法:①MN=HC;②MH= (AH-HB);③MN= (AC+HB);④HN= (HC+HB).其中正确的有 .(填序号) ①②④解析 ∵H为AC的中点,M为AB的中点,N为BC的中点,∴AH=CH= AC,AM=BM= AB,BN=CN= BC,∴MN=MB+BN= (AB+BC)= AC,∴MN=HC,①正确; (AH-HB)= (AB-BH-BH)=MB-HB=MH,②正确;MN= AC,③错误; (HC+HB)= (BC+HB+HB)=BN+HB=HN,④正确.18.(2024甘肃武威九中期末)如图,A、B、C、D是直线上的 四点,M、N分别是AB、CD的中点,且MN=6 cm,BC=4 cm,则 AD= . 8 cm解析 ∵M、N分别是AB、CD的中点,∴AB=2MB,CD=2CN.∵MB+CN=MN-BC=6-4=2(cm),∴AB+CD=2(MB+CN)=2×2=4(cm),∴AD=AB+BC+CD=4+4=8(cm).三、解答题(共46分)19.(新考向·尺规作图)(6分)如图,已知线段a、b.求作:线段AB, 使AB=2a-b.(不写作法,保留作图痕迹) 解析 如图,线段AB即为所求. 20.(2023山东枣庄台儿庄期中)(8分)如图,∠AOC与∠BOC互 为补角,∠BOC与∠BOD互为余角,且∠BOC=4∠BOD.(1)求∠BOC的度数.(2)若OE平分∠AOC,求∠BOE的度数. 解析 (1)∵∠BOC与∠BOD互为余角,∴∠BOC+∠BOD=90°.∵∠BOC=4∠BOD,∴∠BOC= ×90°=72°.(2)∵∠AOC与∠BOC互为补角,∴∠AOC+∠BOC=180°,∴∠AOC=180°-∠BOC=180°-72°=108°.∵OE平分∠AOC,∴∠COE= ∠AOC= ×108°=54°,∴∠BOE=∠COE+∠BOC=54°+72°=126°.21.(10分)知识是用来为人类服务的,我们应该把它们用于有 意义的方面.下面是两个情景,请你作出评判.情景一:如图1,从教学楼到图书馆,总有少数同学不走人行道 而横穿草坪,这是为什么呢?试用所学数学知识来说明这个 问题. 图1情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽 水站向两村供水,问:抽水站修在什么地方才能使所需的管道 最短?请在图2中画出抽水站P的位置,并说明你的理由. 图2你赞同以上哪种做法?你认为应用数学知识为人类服务时应 注意什么?解析 情景一:原因是两点之间的所有连线中,线段最短.情景二:抽水站P的位置如图所示. 理由:两点之间的所有连线中,线段最短.赞同情景二中的做法.应用数学知识为人类服务时应注意不 能以破坏环境为代价.22.(2024吉林九中期末)(10分)如图,C是线段AB上一点,M是 AC的中点,N是BC的中点.(1)若AM=2,BC=6,求MN的长度.(2)若AB=10,求MN的长度. 解析 (1)∵N是BC的中点,M是AC的中点,AM=2,BC=6,∴CN= BC=3,AM=CM=2,∴MN=MC+CN=5.(2)∵M是AC的中点,N是BC的中点,AB=10,∴MN=MC+CN= AC+ BC= AB=5.23.(2024福建福州闽侯期末)(12分)如图1,线段AB=20,CD=3, 点E,F分别是AC,BD的中点.(1)若AC=7,求线段EF的长度.(2)当线段CD在线段AB上运动时,试判断线段EF的长度是否 发生变化,如果不变,求出EF的长度;如果变化,请说明理由.(3)我们发现角的很多规律和线段一样,如图2,OM,ON分别平 分∠GOP和∠HOQ,若∠GOH=130°,∠POQ=18°,求∠MON 的度数. 图1 图2 解析 (1)∵AC=7,AB=20,CD=3,∴BD=AB-AC-CD=10,∵点E,F分别是AC,BD的中点,∴EC= AC=3.5,FD= BD=5,∴EF=EC+CD+DF=11.5.(2)不变.∵AB=20,CD=3,∴BD=AB-AC-CD=17-AC,∵点E,F分别是AC,BD的中点,∴EC= AC,FD= BD= (17-AC),∴EF=EC+CD+DF= AC+3+ (17-AC)=11.5.(3)∵∠GOH=130°,∠POQ=18°,∴∠GOP+∠HOQ=130°-18°=112°,∵OM,ON分别平分∠GOP和∠HOQ,∴∠MOP= ∠GOP,∠QON= ∠HOQ,∴∠MON=∠MOP+∠POQ+∠QON= ∠GOP+ ∠HOQ+∠POQ= (∠GOP+∠HOQ)+∠POQ=56°+18°=74°.
第6章 素养综合检测(满分100分, 限时60分钟)一、选择题(每小题3分,共36分)1.(2024山东济南济阳期中)下列四个几何体中,是棱柱的是 (M7106001)( )A. B. C. D. B解析 选项A中的几何体是圆柱;选项B中的几何体是三棱 柱;选项C中的几何体是三棱锥;选项D中的几何体是四棱台. 故选B.2.(2024山东烟台牟平期中)如图,把图形绕着给定的直线旋 转一周后形成的几何体是(M7106001)( ) A. B. C. D. D3.下面的几何体中,全是由曲的面围成的是(M7106001)( )A.圆柱 B.圆锥 C.球 D.正方体C解析 A.圆柱是由两个平的面和一个曲的面围成的;B.圆锥 是由一个曲的面和一个平的面围成的;C.球是由一个曲的面 围成的;D.正方体是由六个平的面围成的.故选C.4.如图所示的立体图形中,面与面相交所成线的条数是(M71 06001)( ) A.5 B.6 C.4 D.7 B解析 观察题图可得,面与面相交所成的线有6条.故选B.5.(跨学科·语文)(2022河北保定唐县期末)《红楼梦》中有这 么一句话,“自古道:‘千里姻缘一线牵’,管姻缘的有一位 月下老人,预先注定,暗里只用一根红线,把这两个人的脚绊 住.”若这里所说的“线”是真的,则在数学中指的应是( )A.直线 B.射线C.线段 D.以上都不对C解析 由题意可知,两个人可以看作两个点,所以若这里所说 的“线”是真的,则在数学中指的应是线段.故选C.6.(2024山东菏泽月考)用一个平面去截下列几何体,截得的 平面图形可能是三角形的有(M7106001)( ) A.0个 B.1个 C.2个 D.3个D解析 三棱柱、圆锥、四棱柱的截面都有可能是三角形,圆 柱的截面不可能是三角形,故选D.7.(2024山西晋中期末)下列说法与如图所示的几何图形相符 的是( ) A.点D在线段CB的延长线上B.∠1可以表示成∠CC.射线BD与射线CD表示同一条射线D.∠1+∠ACD=180° D解析 A.点D在线段BC的延长线上,所以A中说法错误;B.∠1 不可以表示成∠C,所以B中说法错误;C.射线BD与射线CD是 两条射线,所以C中说法错误;D.∠1+∠ACD=180°,所以D中 说法正确.故选D.8.点P在直线a上,也在直线b上,但不在直线c上,且直线a、b、 c两两相交,下列符合上述条件的图形是 ( ) A B C D D解析 观察选项中的图形可知只有D选项符合题意,故选D.9.射线OA上有B、C两点,若OB=8,BC=2,线段OB、BC的中点 分别为D、E,则线段DE的长为 ( )A.5 B.1或3 C.1 D.5或3 D解析 因为OB=8,D是OB的中点,所以DB=4,因为BC=2,E是BC的中点,所以BE=1.如图1,DE=BD-BE=3;如图2,DE=BD+BE=5.所以DE的长为5或3.故选D. 图1 图2 10.(情境题·中华优秀传统文化)曲桥是我国古代经典建筑之 一,它的修建增加了游人在桥上行走的路程,有利于游人更好 地观赏风光.两地间修建曲桥与修建直的桥相比,增加了桥的 长度,蕴含的数学道理是(M7101003)( )A.两点之间,线段最短B.两点确定一条直线C.经过一点可以作无数条直线D.连接两点间线段的长度叫作两点间的距离A解析 根据线段的性质可知,两地间修建曲桥与修建直的桥 相比,增加了桥的长度,蕴含的数学道理是两点之间,线段最 短,故选A.11.(2024山东潍坊潍城期中)小亮正确完成了以下两道作图 题:①延长线段AB到C,使BC=AB.②反向延长线段DE到F,使 点D是线段EF的一个三等分点.针对小亮的作图,小莹说: “点B是线段AC的中点.”小轩说:“DE=2DF.”下列说法正 确的是( )A.小莹、小轩都对B.小莹不对,小轩对C.小莹、小轩都不对D.小莹对,小轩不对D解析 延长线段AB到C,使BC=AB,如图①所示,此时点B是线 段AC的中点.反向延长线段DE到F,使点D是线段EF的一个 三等分点,如图②所示,有两种情况,有DE=2DF或DE= DF.因此小莹说得对,小轩说得不对.故选D. 图① 图②12.如图,已知∠AOB=180°,∠AOC=110°,现将射线OA绕点O 顺时针匀速旋转,射线OB保持不动,当射线OA与射线OB重合 时停止旋转.当三条射线构成的角中有两个角相等(重合除 外)时,射线OA旋转的角度为 ( ) A.40° B.60°C.40°或145° D.60°或150°C解析 经分析,三条射线构成的角中有两个角相等(重合除 外)时,存在以下两种情形:①当射线OA旋转到∠BOC的外部 时,∠AOC=∠BOC=70°,此时射线OA旋转的角度为110°-70°=40°.②当射线OA旋转到∠BOC的内部时,∠AOC=∠AOB,此 时∠AOB= ∠BOC=35°,射线OA旋转的角度为180°-35°=145°.综上,射线OA旋转的角度为40°或145°.故选C.二、填空题(每小题3分,共18分)13.(2022山东济南期末)计算:30°12'= °.30.2解析 因为1°=60',所以12'=0.2°,所以30°12'=30.2°.14.如图①,A点为公交车车站,点B、C、D为三家在同一条直 线上的医院,E点为医护人员住宿楼,公交车完成接送任务需 返回车站,则在送医护人员回住宿楼的过程中,最近的路线为 A→B→C→D→E→A(如图②),其根据是 . 两点之间,线段最短解析 在送医护人员回住宿楼的过程中,最近的路线为A→B →C→D→E→A,其依据是两点之间,线段最短.15.(2024山东德州平原期末)如图,点O在直线AB上,射线OF 平分∠AOD,∠EOF=∠AOC=90°,在图中与∠AOF互余的角 一共有 个.(M7106006) 3解析 ∵射线OF平分∠AOD,∴∠AOF=∠DOF,∵∠EOF=∠AOC=90°,∴∠AOF+∠COF=∠AOC=90°,∠AOF+∠BOE=180°-∠EOF =90°,∠DOF+∠DOE=∠EOF=90°,∴与∠AOF互余的角有∠COF,∠BOE,∠DOE,共3个,故答案 为3.16.(2024山东聊城东昌府期中)线段AB上有P、Q两点,AB=26,AP=14,PQ=11,那么BQ= . 23或1解析 本题有两种情形:①当点Q在线段AP上时,如图,BQ=BP+PQ=AB-AP+PQ=26-14+11=23; ②当点Q在线段BP上时,如图,BQ=BP-PQ=AB-AP-PQ=26-14- 11=1. 故答案为23或1.17.如图,点A、B、C在同一直线上,H为AC的中点,M为AB的 中点,N为BC的中点,则下列说法:①MN=HC;②MH= (AH-HB);③MN= (AC+HB);④HN= (HC+HB).其中正确的有 .(填序号) ①②④解析 ∵H为AC的中点,M为AB的中点,N为BC的中点,∴AH=CH= AC,AM=BM= AB,BN=CN= BC,∴MN=MB+BN= (AB+BC)= AC,∴MN=HC,①正确; (AH-HB)= (AB-BH-BH)=MB-HB=MH,②正确;MN= AC,③错误; (HC+HB)= (BC+HB+HB)=BN+HB=HN,④正确.18.(2024甘肃武威九中期末)如图,A、B、C、D是直线上的 四点,M、N分别是AB、CD的中点,且MN=6 cm,BC=4 cm,则 AD= . 8 cm解析 ∵M、N分别是AB、CD的中点,∴AB=2MB,CD=2CN.∵MB+CN=MN-BC=6-4=2(cm),∴AB+CD=2(MB+CN)=2×2=4(cm),∴AD=AB+BC+CD=4+4=8(cm).三、解答题(共46分)19.(新考向·尺规作图)(6分)如图,已知线段a、b.求作:线段AB, 使AB=2a-b.(不写作法,保留作图痕迹) 解析 如图,线段AB即为所求. 20.(2023山东枣庄台儿庄期中)(8分)如图,∠AOC与∠BOC互 为补角,∠BOC与∠BOD互为余角,且∠BOC=4∠BOD.(1)求∠BOC的度数.(2)若OE平分∠AOC,求∠BOE的度数. 解析 (1)∵∠BOC与∠BOD互为余角,∴∠BOC+∠BOD=90°.∵∠BOC=4∠BOD,∴∠BOC= ×90°=72°.(2)∵∠AOC与∠BOC互为补角,∴∠AOC+∠BOC=180°,∴∠AOC=180°-∠BOC=180°-72°=108°.∵OE平分∠AOC,∴∠COE= ∠AOC= ×108°=54°,∴∠BOE=∠COE+∠BOC=54°+72°=126°.21.(10分)知识是用来为人类服务的,我们应该把它们用于有 意义的方面.下面是两个情景,请你作出评判.情景一:如图1,从教学楼到图书馆,总有少数同学不走人行道 而横穿草坪,这是为什么呢?试用所学数学知识来说明这个 问题. 图1情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽 水站向两村供水,问:抽水站修在什么地方才能使所需的管道 最短?请在图2中画出抽水站P的位置,并说明你的理由. 图2你赞同以上哪种做法?你认为应用数学知识为人类服务时应 注意什么?解析 情景一:原因是两点之间的所有连线中,线段最短.情景二:抽水站P的位置如图所示. 理由:两点之间的所有连线中,线段最短.赞同情景二中的做法.应用数学知识为人类服务时应注意不 能以破坏环境为代价.22.(2024吉林九中期末)(10分)如图,C是线段AB上一点,M是 AC的中点,N是BC的中点.(1)若AM=2,BC=6,求MN的长度.(2)若AB=10,求MN的长度. 解析 (1)∵N是BC的中点,M是AC的中点,AM=2,BC=6,∴CN= BC=3,AM=CM=2,∴MN=MC+CN=5.(2)∵M是AC的中点,N是BC的中点,AB=10,∴MN=MC+CN= AC+ BC= AB=5.23.(2024福建福州闽侯期末)(12分)如图1,线段AB=20,CD=3, 点E,F分别是AC,BD的中点.(1)若AC=7,求线段EF的长度.(2)当线段CD在线段AB上运动时,试判断线段EF的长度是否 发生变化,如果不变,求出EF的长度;如果变化,请说明理由.(3)我们发现角的很多规律和线段一样,如图2,OM,ON分别平 分∠GOP和∠HOQ,若∠GOH=130°,∠POQ=18°,求∠MON 的度数. 图1 图2 解析 (1)∵AC=7,AB=20,CD=3,∴BD=AB-AC-CD=10,∵点E,F分别是AC,BD的中点,∴EC= AC=3.5,FD= BD=5,∴EF=EC+CD+DF=11.5.(2)不变.∵AB=20,CD=3,∴BD=AB-AC-CD=17-AC,∵点E,F分别是AC,BD的中点,∴EC= AC,FD= BD= (17-AC),∴EF=EC+CD+DF= AC+3+ (17-AC)=11.5.(3)∵∠GOH=130°,∠POQ=18°,∴∠GOP+∠HOQ=130°-18°=112°,∵OM,ON分别平分∠GOP和∠HOQ,∴∠MOP= ∠GOP,∠QON= ∠HOQ,∴∠MON=∠MOP+∠POQ+∠QON= ∠GOP+ ∠HOQ+∠POQ= (∠GOP+∠HOQ)+∠POQ=56°+18°=74°.
相关资料
更多









