北师大版（2024）数学七年级上册 同步备课第五章 小结与复习 课件

这是一份北师大版（2024）数学七年级上册 同步备课第五章 小结与复习 课件，共31页。

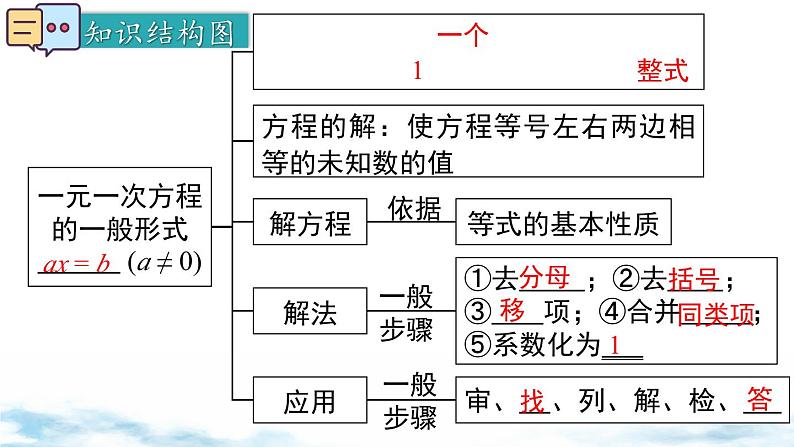
小结与复习 第五章 一元一次方程 七年级上册数学（北师版）一元一次方程的一般形式 (a ≠ 0)定义：只含有 未知数，未知数的次数都是 ，等式两边都是____方程的解：使方程等号左右两边相等的未知数的值解方程等式的基本性质解法应用①去 ；②去 ；③ 项；④合并 ；⑤系数化为___审、 、列、解、检、 ax = b一个1整式分母括号移同类项1找答一、方程的有关概念1. 方程：含有未知数的等式叫作方程．2. 一元一次方程的概念：如果只含有___个未知数(元)，未知数的次数都是 ，等式两边都是________，这样的方程叫作一元一次方程.3. 方程的解：使方程等号左右两边相等的未知数的 值叫作方程的解．4. 解方程：求方程的解的过程叫作解方程．一1整式二、等式的基本性质 bcc解一元一次方程的一般步骤： (1) 去分母：方程两边都乘各分母的最小公倍数，别 漏乘。 (2) 去括号：注意括号前的系数与符号。 (3) 移项：把含有未知数的项移到方程的左边，常数 项移到方程右边，移项时注意要改变符号。 (4) 合并同类项：把方程化成 ax＝b (a ≠ 0) 的形式． (5) 系数化为 1：方程两边同除以 x 的系数，得 x＝m 的形式。三、一元一次方程的解法 1. 列一元一次方程解决实际问题的一般步骤： 审：审清题意，分清题中的已知量、未知量。 设：设未知数，设其中某个未知量为 x。 列：根据题意寻找等量关系列方程。 解：解方程。 检：检验方程的解是否符合题意。 答：写出答案 (包括单位)。四、实际问题与一元一次方程2. 常见的几种方程类型及等量关系： (1) 行程问题中基本量之间关系： 路程＝速度×时间． ① 相遇问题： 全路程＝甲走的路程＋乙走的路程； ② 追及问题： 甲为快者，被追路程＝甲走路程－乙走路程； ③ 流水行船问题： v顺＝v静＋v水，v逆＝v静－v水。(2) 工程问题中基本量之间的关系： ① 工作量＝工作效率×工作时间； ② 合作的工作效率＝工作效率之和； ③ 工作总量＝各部分工作量之和＝合作的工作效 率×工作时间； ④ 在没有具体数值的情况下，通常把工作总量看 作 1。(3) 销售问题与方案选择问题 ① 商品利润＝商品售价－商品进价；④ 商品售价＝商品进价＋商品利润 ＝商品进价＋商品进价×利润率 ＝商品进价×(1＋利润率)。例1 有式子：① 2x + 4 = 6，② x - 1 = ，③ 3x2 - 2x = 0，④ 5x < 7，⑤ 3x - 2y = 2，⑥ x = 3，其中是一元一次方程的有 ( )A. 5 个 B. 4 个 C. 3 个 D. 2 个D√分析：② 等号右边不是整式；√③ 未知数次数不为 1 ；④ 不是等式；⑤ 含两个未知数.1. 下列方程中，是一元一次方程的是 ( )A. = 2 B. x + 2 = y + 2 C. x - 1 = 2x D. x2 - 1 = 0C2. 如果方程 kx|k+1| + 2 = 0 是关于 x 的一元一次方程，那么 k = .分析：k ≠ 0，|k + 1| = 1，解得 k = -2 或 k = 0 (舍).-2例2 根据等式的基本性质，下列各式变形正确的是 ( )A.若 3x = 5，则 =B.若 x = y，则 x - 6 = 6 - yC.如果 x = y，那么 -8x = -8yD. 2x = 6，那么 x =C(a ≠ 0)y - 633. (兰州市第二十中学期末) 下列等式变形中不正确的是 ( )A. 若 x = y，则 x + 5 = y + 5B. 若 = ，则 x = yC. 若 -3x = -3y，则 x = yD. 若 mx = my，则 x = yD(m ≠ 0)例3 (1) 解：去分母，得 2(2x - 1) - (10x + 1) = 12去括号，得 4x - 2 - 10x - 1 = 12移项，得 4x - 10x = 12 + 2 + 1合并同类项，得 -6x = 15系数化为 1，得 x = -2.5 .(2) 去分母，得 2(3x - 5) + 9 = 5 + 4x去括号，得 6x - 10 + 9 = 5 + 4x移项，得 6x - 4x = 5 + 10 - 9合并同类项，得 x = 3.分子分母同时乘10，分数大小不变小数化分数4. (高台县城关初级中学期末) 解方程： (1) 3(1 - x) = 1 + 2x 解：去括号，得 3 - 3x = 1 + 2x移项，得 -3x - 2x = 1 - 3合并同类项，得 -5x = -2系数化为 1，得 x = 0.4 .解：去分母，得 5(3x + 1) - 2(4x - 2) = -10 去括号，得 15x + 5 - 8x + 4 = -10移项，得 15x - 8x = -10 - 5 - 4合并同类项，得 7x = -19 (2)例4 客车和货车同时从甲、乙两地的中点反向行驶，3 小时后，客车到达甲地，货车离乙地还有 30 千米. 如果客车与货车的速度的比为 4 ∶3，那么甲、乙两地相距多少千米？客车、货车每小时分别行驶多少千米？分析：问 v客车 v货车4x km/h3x km/h客车路程货车路程30 km◊行程问题解：设客车每小时行驶 4x 千米，货车每小时行驶 3x 千米，由题意，得3×4x＝3×3x＋30解得 x＝10.所以 4x＝40，3x＝30，2×3×4x＝240.答：甲、乙两地相距 240 千米，客车每小时行驶 40 千米，货车每小时行驶 30 千米.5. (甘肃山丹期末) 轮船沿江从 A 港顺流行驶到 B 港，比从 B 港返回 A 港少用 3 小时，若船速为 26 千米/时，水速为 2 千米/时，求 A 港和 B 港相距多少千米. 设 A 港和 B 港相距 x 千米. 根据题意，可列出的方程是 ( )A例5 (甘肃肃州期末) 甲、乙两工程队开挖一条水渠各需 10 天、15 天，两队合作 2 天后，甲有其他任务，剩下的工作由乙队单独做，还需多少天能完成任务？设还需 x 天，可得方程 ( )A. B.C. D.A◊工程问题6. (安徽定远期末) 整理一批图书，由一个人做要 40 小时完成，现计划由一部分人先做 4 小时，再增加 2 人和他们一起做 8 小时，完成这项工作. 假设这些人的工作效率相同，具体应先安排多少人工作？解：设应先安排 x 人工作，由题意，得解得 x = 2.答：应先安排 2 人工作.例6 某文教店购进一批钢笔，按进价提高 40% 后标价，为了增加销量，文教店决定按标价打八折出售，这时每支钢笔的售价为 28 元.(1) 求每支钢笔的进价为多少元；解：设每支钢笔的进价为 x 元，由题意，得0.8×(1 + 40%)x = 28解得 x = 25.答：每支钢笔的进价为 25 元 .◊销售问题(2) 该文教店卖出这批钢笔的一半后，决定将剩下的钢笔以每 3 支 80 元的价格出售，很快销售完毕，销售这批钢笔文教店共获利 2800 元，求该文教店共购进这批钢笔多少支？解：设该文教店共购进这批钢笔 x 支，由题意，得解得 x = 1200.解：该文教店共购进这批钢笔 1200 支.7. 一件衣服标价 132 元，若以 9 折降价出售，仍可获利 10%，则这件衣服的进价是 元.(1＋10%)x＝132×0.9108◊方案选择问题例7 有两种通讯套餐，收费方式如表：(1) 一个月通话多少分钟时，两种套餐收费相同？解：(1) 设一个月的通话 x 分钟时，两种收费方式相同，根据题意，得 30 + 0.15x = 0.3x解得 x = 200.答：一个月的通话 200 分钟时，两种套餐收费相同.(2) 一个月内在本地通话 100 分钟，选择___套餐更划算；一个月内在本地通话 300 分钟，选择___套餐更划算.A：30 + 0.15×100 = 45 (元)B：0.3×100 = 30 (元)A：30 + 0.15×300 = 75 (元)B：0.3×300 = 90 (元)BA8. (宁波·期中) 为庆祝“五一”，学校统一组织合唱比赛，七、八年级共 92 人 (其中七年级的人数超过 46 人但不足 90 人) 准备统一购买服装参加比赛. 若两个年级分别单独购买服装一共应付 5000 元， 下表是某服装厂给出服装的价格表：(1) 求七、八年级各有多少学生参加合唱比赛；解：(1) 设七年级有 x 人，则八年级有 (92 - x) 人，因为七年级人数超过 46 但不足 90 人，所以八年级人数不足 46 人.依题意，得 50x + 60(92 - x) = 5000解得 x = 52.则 92 - x = 40.答：七年级有 52 人，则八年级有 40 人参加合唱比赛.(2) 七年级参加合唱比赛的学生中，有 10 名同学抽调去参加绘画比赛，不能参加合唱比赛，请你为两个年级设计一种最省钱的购买服装方案.(2) 七年级：52 - 10 = 42 （人），八年级： 40 人.①两个年级单独购买：②两个年级一起买 82 套：③两个年级一起买 91 套：42×60 + 40×60 = 4920 (元)82×50 = 4100 (元)91×40 = 3640 (元)因为 4920 > 4100 > 3640，所以两个年级一起买 91 套最省钱.实际问题实际问题的解答一元一次方程的解 (x = a)一元一次方程抽象为数学模型回归于实际问题