北师大版（2024）4 有理数的乘方教课ppt课件

这是一份北师大版（2024）4 有理数的乘方教课ppt课件，文件包含241有理数的乘方pptx、241mp4等2份课件配套教学资源，其中PPT共20页， 欢迎下载使用。

1．通过现实背景，理解有理数乘方的意义，体会乘方与乘法的联系，感受数学的简洁美。2．通过能准确说出有理数乘方中底数、指数和幂，能准确计算有理数的乘方，发展应用意识。3．通过经历观察、类比、归纳得出有理数乘方的运算法则的过程，领会重要的数学建模思想、归纳思想，形成数感、符号感，发展抽象思维。
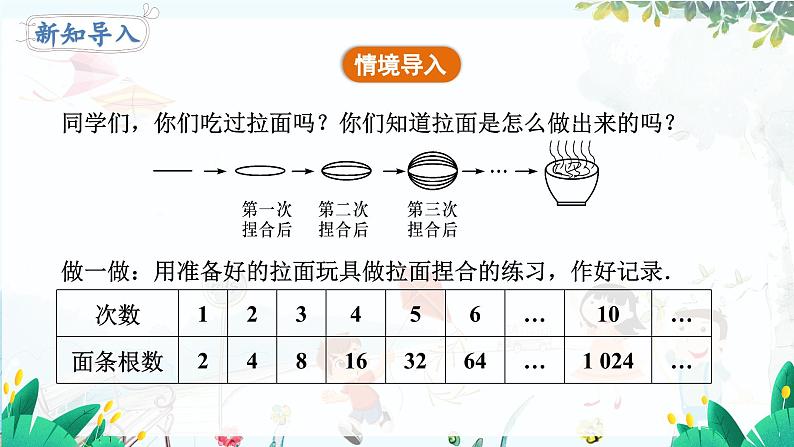
同学们，你们吃过拉面吗？你们知道拉面是怎么做出来的吗？
做一做：用准备好的拉面玩具做拉面捏合的练习，作好记录．
由“棋盘摆米”游戏导入新课，下图是国际象棋棋盘的图片，把它抽象成8×8的64格的小正方形，让学生尝试摆米，并试着观察出规律，看看第64格里会放多少粒米？
思考问题“某种细胞每0.5小时由1个分裂成2个，经过5小时这种细胞由1个能分裂成多少个？若经过了n次分裂呢？”
1．请同学们阅读教材58－59页，思考并回答下列问题。（1）什么是乘方？什么是幂？什么是底数和指数？（2）an读作什么？（3）一个数的幂的符号如何确定？
求n个相同因数a的积的运算叫作乘方，乘方的结果叫作幂，a叫作底数，n叫作指数
正数的任何次幂都是正数，负数的偶次幂是正数，负数的奇次幂是负数
a的n次幂或a的n次方
2．请同学们在完成上面任务后思考以下问题。（1）（－2）4与－24一样吗？为什么？
不一样，（－2）4表示－2的4次方，－24表示2的4次方的相反数
把一张纸进行如下操作：①对折2次可裁成4张，即2×2张。②对折3次可裁成8张，即2×2×2张。问题：(1)对折10次可裁成几张？请用一个算式表示（不用算出结果）；（2）对折100次裁成的张数可以表示为式子中有多少个2相乘？
对折10次裁成的张数可以表示为2×2×2×2×2×2×2×2×2×2
提疑惑：你有什么疑惑？
知识点1：乘方的意义（重点）
1．有理数乘方的符号法则：（1）正数的任何次幂都是正数；（2）负数的奇次幂是负数，负数的偶次幂是正数；（3）0的任何正整数次幂都是0。2．计算一个有理数的乘方时，先根据乘方的符号法则确定幂的符号，再计算绝对值。有理数的乘方运算也可以转化为有理数的乘法运算，按照有理数的乘法法则计算。
知识点2：乘方的运算法则（重难点）
【题型一】利用乘方的意义认识乘方
例1：n3可以表示成（　 　）A．3个n相乘 B．n个3相乘 C．3个n相加 D．n个3相加
【题型二】有理数乘方的运算
例3：下列算式中，运算结果为负数的是（　 　）A．－（－8）3 B．－24 C．－（－3）3 D．（－2）2例4：计算：
【题型三】利用乘方的意义探究非负性
例5：已知（a－3）2＋|b＋1|＝0，则a2＋b2＝　 　。
A．1 B．－1 C．2 024 D．－2 024
【题型四】利用乘方的意义探索规律
例6：一根1 m长的绳子，第一次剪去一半，第二次剪去剩下的一半，如此剪下去，第六次后剩下的绳子长度为______m。
例7：在计算1＋2＋22＋23＋…＋299＋2100时，可以先设S＝1＋2＋22＋23＋…＋299＋2100，然后在等式两边同乘以2，则有2S＝2＋22＋23＋24＋…＋2100＋2101，最后两式相减可得2S－S＝（2＋22＋23＋24＋…＋2100＋2101）－（1＋2＋22＋23＋…＋299＋2100）＝2101－1，即S＝2101－1，所以1＋2＋22＋23＋…＋299＋2100＝2101－1。根据以上方法，计算：
同学们，今天这节课我们主要学习了哪些知识？
乘方的意义，乘方的运算，乘方意义的应用
今天的内容，难度不大，但极容易出错，课上已经强调了易错点，同学们在课后的练习过程中，一定要警惕，小心这些易错点钻空子，相信同学们都能全部做对，加油！