高中人教A版 (2019)10.1 随机事件与概率达标测试

这是一份高中人教A版 (2019)10.1 随机事件与概率达标测试，共16页。试卷主要包含了概念，随机试验的特点等内容，欢迎下载使用。

（一）随机试验
1.概念：对随机现象的实现和对它的观察称为随机试验，简称试验，常用字母E表示.
2.随机试验的特点
(1)试验可以在相同条件下重复进行；
(2)试验的所有可能结果是明确可知的，并且不止一个；
(3)每次试验总是恰好出现这些可能结果中的一个，但事先不能确定出现哪一个结果.
（二）样本空间
随机试验E的每个可能的基本结果称为样本点，全体样本点的集合称为试验E的样本空间，一般地，用Ω表示样本空间，用ω表示样本点，如果一个随机试验有n个可能结果ω1，ω2，…，ωn，则称样本空间Ω＝{ω1，ω2，…，ωn}为有限样本空间.
（三）随机事件、必然事件与不可能事件
1.一般地，随机试验中的每个随机事件都可以用这个试验的样本空间的子集来表示，为了叙述方便，我们将样本空间Ω的子集称为随机事件，简称事件，并把只包含一个样本点的事件称为基本事件.当且仅当A中某个样本点出现时，称为事件A发生.
2.Ω作为自身的子集，包含了所有的样本点，在每次试验中总有一个样本点发生，所以Ω总会发生，我们称Ω为必然事件.
3.空集∅不包含任何样本点，在每次试验中都不会发生，我们称为∅为不可能事件.
二．事件的关系和运算
三．事件的运算
四．古典概型
1.随机事件的概率：对随机事件发生可能性大小的度量(数值)称为事件的概率，事件A的概率用P(A)表示.
2.古典概型
一般地，若试验E具有以下特征：
(1)有限性：样本空间的样本点只有有限个；
(2)等可能性：每个样本点发生的可能性相等.
称试验E为古典概型试验，其数学模型称为古典概率模型，简称古典概型.
3.古典概型的概率公式
一般地，设试验E是古典概型，样本空间Ω包含n个样本点，事件A包含其中的k个样本点，则定义事件A的概率
概率的性质
性质1 对任意的事件A，都有P(A)≥0.
性质2 必然事件的概率为1，不可能事件的概率为0，即P(Ω)＝1，P(∅)＝0.
性质3 如果事件A与事件B互斥，那么P(A∪B)＝P(A)＋P(B).
性质4 如果事件A与事件B互为对立事件，那么P(B)＝1－P(A)，P(A)＝1－P(B).
性质5 如果A⊆B，那么P(A)≤P(B).
性质6 设A，B是一个随机试验中的两个事件，我们有P(A∪B)＝P(A)＋P(B)－P(A∩B).
知识简用
题型一 事件类型的判断
【例1-1】（2022·广东）以下事件是随机事件的是（ ）
A．标准大气压下，水加热到，必会沸腾B．走到十字路口，遇到红灯
C．长和宽分别为的矩形，其面积为D．实系数一元一次方程必有一实根
【例1-2】（2022春·黑龙江哈尔滨·高一哈尔滨市第一二二中学校校考期末）下列事件是必然事件的是（ ）
A．在标准大气压下，水加热到时会沸腾
B．实数的绝对值不小于零
C．某彩票中奖的概率为，则买10000张这种彩票一定能中奖
D．连续两次抛掷一枚骰子，两次都出现2点向上
题型二 样本空间
【例2-1】（2023·高一课时练习）写出从集合任取两个元素构成子集的样本空间．
【例2-2】（2023·高一课时练习）袋中放有4个白球、2个黑球，写出“从中取出2个球”的等可能的样本空间．
【例2-3】（2022春·广东揭阳·高一校考阶段练习）有两颗正四面体的玩具，其四个面上分别标有数字1，2，3，4，下面做投掷这两颗正四面体玩具的试验：用表示结果，其中表示第1颗正四面体玩具出现的点数，表示第2颗正四面体玩具出现的点数.试写出：（以下各小题先回答基本事件数目，再具体作答）
(1)试验的基本事件；
(2)事件“出现点数之和大于3”包含的基本事件；
(3)事件“出现点数相等”包含的基本事件.
题型三 事件的关系
【例3-1】（2023吉林长春）盒子中装有红色，黄色和黑色小球各2个，一次取出2个小球，下列事件中，与事件“2个小球都是红色”对立的事件是（ ）
A．2个小球都是黑色B．2个小球恰有1个是红色
C．2个小球都不是红色D．2个小球至多有1个是红色
【例3-2】（2022上海）已知事件A､B､C满足，，则下列说法不正确的是（ ）
A．事件A发生一定导致事件C发生B．事件B发生一定导致事件C发生
C．事件发生不一定导致事件发生D．事件发生不一定导致事件发生
题型四 事件的运算
【例4-1】（2022·全国·高一专题练习）抛掷一枚骰子，“向上的面的点数是1或2”为事件，“向上的面的点数是2或3”为事件，则（ ）
A．B．
C．表示向上的面的点数是1或2或3D．表示向上的面的点数是1或2或3
【例4-2】（2022·高一单元测试）某小组有3名男生和2名女生，从中任选2名参加演讲比赛，设={2名全是男生}，{2名全是女生}，{恰有一名男生}，{至少有一名男生}，则下列关系不正确的是（ ）
A．B．C．D．
题型五 古典概型的判断
【例5-1】（2022·高一单元测试）以下试验不是古典概型的有（ ）
A．从6名同学中，选出4名参加学校文艺汇演，每个人被选中的可能性大小
B．同时掷两枚骰子，点数和为7的概率
C．近三天中有一天降雪的概率
D．3个人站成一排，其中甲，乙相邻的概率
【例5-2】（2022·高一课时练习）下列试验是古典概型的是（ ）
A．在平面直角坐标系内，从横坐标和纵坐标都是整数的所有点中任取一点
B．某射手射击一次，可能命中0环，1环，2环，…，10环
C．某小组有男生5人，女生3人，从中任选1人做演讲
D．在适宜的条件下，种下一粒种子，观察它是否发芽
题型六 古典概型的样本空间
【例6-1】（2023·陕西铜川）某活动小组由2名男同学与3名女同学组成，他们完成一项活动后，要从这5名同学中选2人写活动体会，则所选2人中没有男生的概率为（ ）
A．B．C．D．
【例6-2】（2023·高一课时练习）从一个装有2黄2绿的袋子里，
(1)有放回的摸球两次,两次摸到的都是绿球的概率是多少？
(2)不放回的摸球两次,两次摸到的都是绿球的概率是多少？
题型七 概率的性质
【例7-1】（2022·全国·高一期末）甲、乙两位同学进行羽毛球比赛，约定五局三胜制（无平局），已知甲每局获胜的概率都为，且前两局以领先，则最后甲获胜的概率为（ ）
A．B．C．D．
【例7-2】（2023·全国·高一专题练习）已知，，如果，那么（ ）
A．0.7B．0.6C．0.4D．0.3
【例7-3】．（2022·全国·高三专题练习）已知随机事件，，中，与互斥，与对立，且，，则（ ）
A．0.3B．0.6C．0.7D．0.8
【例7-4】（2022·高一课时练习）班级新年晚会设置抽奖环节．不透明纸箱中有大小、质地相同的红球3个(编号为1，2，3)，黄球2个(编号为4，5)，有如下两种方案可供选择：
方案一：一次性抽取2个球，若颜色相同，则获得奖品；
方案二：依次无放回地抽取2个球，若颜色相同，则获得奖品；
方案三：依次有放回地抽取2个球，若编号的数字之和大于5，则获得奖品．
(1)分别写出按方案一和方案二抽奖的所有样本点；
(2)哪种方案获得奖品的可能性更大？并说明理由．定义
符号
图示
包含关系
一般地，若事件A发生，则事件B一定发生，称事件B包含事件A(或事件A包含于事件B)
B⊇A(或A⊆B)
相等关系
如果事件B包含事件A，事件A也包含事件B，即B⊇A且A⊇B，则称事件A与事件B相等
A＝B
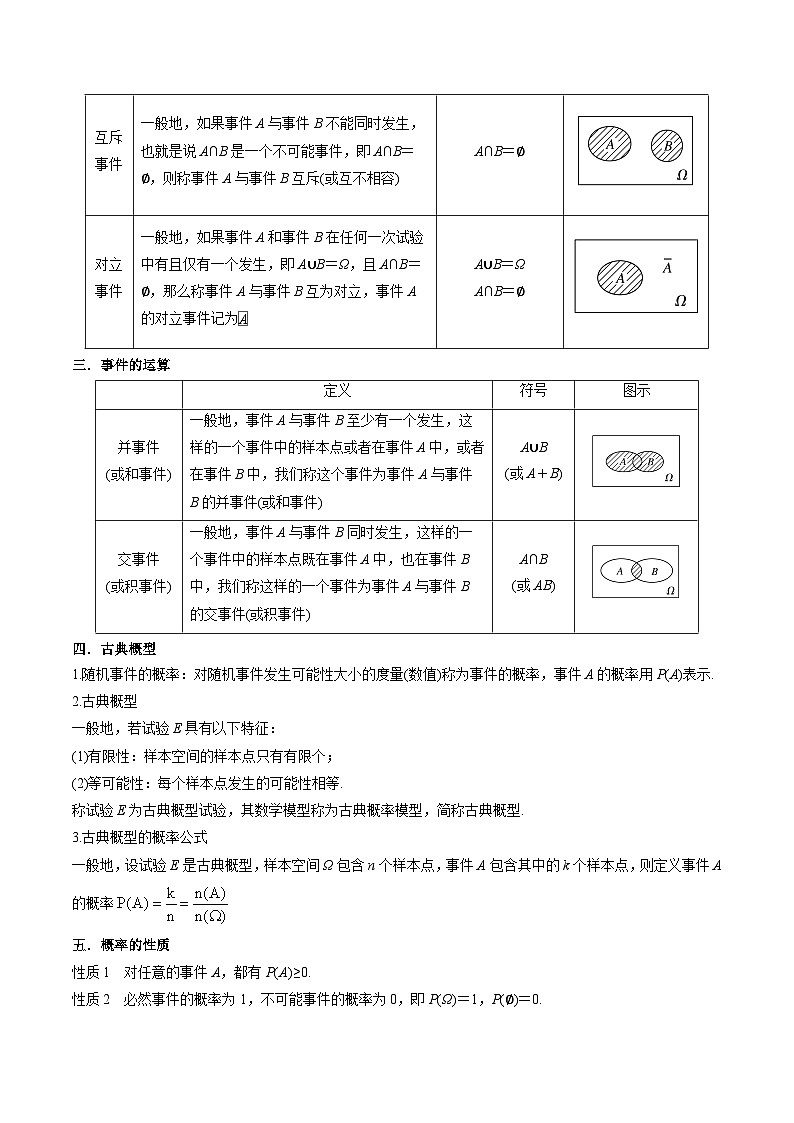
互斥事件
一般地，如果事件A与事件B不能同时发生，也就是说A∩B是一个不可能事件，即A∩B＝∅，则称事件A与事件B互斥(或互不相容)
A∩B＝∅
对立事件
一般地，如果事件A和事件B在任何一次试验中有且仅有一个发生，即A∪B＝Ω，且A∩B＝∅，那么称事件A与事件B互为对立，事件A的对立事件记为eq \x\t(A)
A∪B＝Ω
A∩B＝∅
定义
符号
图示
并事件
(或和事件)
一般地，事件A与事件B至少有一个发生，这样的一个事件中的样本点或者在事件A中，或者在事件B中，我们称这个事件为事件A与事件B的并事件(或和事件)
A∪B
(或A＋B)
交事件
(或积事件)
一般地，事件A与事件B同时发生，这样的一个事件中的样本点既在事件A中，也在事件B中，我们称这样的一个事件为事件A与事件B的交事件(或积事件)
A∩B
(或AB)
10.1 随机事件与概率（学案）知识自测
一．有限样本空间与随机事件
（一）随机试验
1.概念：对随机现象的实现和对它的观察称为随机试验，简称试验，常用字母E表示.
2.随机试验的特点
(1)试验可以在相同条件下重复进行；
(2)试验的所有可能结果是明确可知的，并且不止一个；
(3)每次试验总是恰好出现这些可能结果中的一个，但事先不能确定出现哪一个结果.
（二）样本空间
随机试验E的每个可能的基本结果称为样本点，全体样本点的集合称为试验E的样本空间，一般地，用Ω表示样本空间，用ω表示样本点，如果一个随机试验有n个可能结果ω1，ω2，…，ωn，则称样本空间Ω＝{ω1，ω2，…，ωn}为有限样本空间.
（三）随机事件、必然事件与不可能事件
1.一般地，随机试验中的每个随机事件都可以用这个试验的样本空间的子集来表示，为了叙述方便，我们将样本空间Ω的子集称为随机事件，简称事件，并把只包含一个样本点的事件称为基本事件.当且仅当A中某个样本点出现时，称为事件A发生.
2.Ω作为自身的子集，包含了所有的样本点，在每次试验中总有一个样本点发生，所以Ω总会发生，我们称Ω为必然事件.
3.空集∅不包含任何样本点，在每次试验中都不会发生，我们称为∅为不可能事件.
二．事件的关系和运算
三．事件的运算
四．古典概型
1.随机事件的概率：对随机事件发生可能性大小的度量(数值)称为事件的概率，事件A的概率用P(A)表示.
2.古典概型
一般地，若试验E具有以下特征：
(1)有限性：样本空间的样本点只有有限个；
(2)等可能性：每个样本点发生的可能性相等.
称试验E为古典概型试验，其数学模型称为古典概率模型，简称古典概型.
3.古典概型的概率公式
一般地，设试验E是古典概型，样本空间Ω包含n个样本点，事件A包含其中的k个样本点，则定义事件A的概率
概率的性质
性质1 对任意的事件A，都有P(A)≥0.
性质2 必然事件的概率为1，不可能事件的概率为0，即P(Ω)＝1，P(∅)＝0.
性质3 如果事件A与事件B互斥，那么P(A∪B)＝P(A)＋P(B).
性质4 如果事件A与事件B互为对立事件，那么P(B)＝1－P(A)，P(A)＝1－P(B).
性质5 如果A⊆B，那么P(A)≤P(B).
性质6 设A，B是一个随机试验中的两个事件，我们有P(A∪B)＝P(A)＋P(B)－P(A∩B).
知识简用
题型一 事件类型的判断
【例1-1】（2022·广东）以下事件是随机事件的是（ ）
A．标准大气压下，水加热到，必会沸腾B．走到十字路口，遇到红灯
C．长和宽分别为的矩形，其面积为D．实系数一元一次方程必有一实根
【答案】B
【解析】A．标准大气压下，水加热到100℃必会沸腾，是必然事件；故本选项不符合题意；
B．走到十字路口，遇到红灯，是随机事件；故本选项符合题意；
C．长和宽分别为的矩形，其面积为是必然事件；故本选项不符合题意；
D．实系数一元一次方程必有一实根，是必然事件．故本选项不符合题意．
故选：B．
【例1-2】（2022春·黑龙江哈尔滨·高一哈尔滨市第一二二中学校校考期末）下列事件是必然事件的是（ ）
A．在标准大气压下，水加热到时会沸腾
B．实数的绝对值不小于零
C．某彩票中奖的概率为，则买10000张这种彩票一定能中奖
D．连续两次抛掷一枚骰子，两次都出现2点向上
【答案】B
【解析】因为在标准大气压下，水加热到才会沸腾，所以A不是必然事件；
因为实数的绝对值不小于零，所以B是必然事件；
因为某彩票中奖的概率为，仅代表可能性，所以买100000张这种彩票不一定能中奖，即C不是必然事件；抛掷骰子，每一面出现都是随机的，所以D是随机事件．故选：B．
题型二 样本空间
【例2-1】（2023·高一课时练习）写出从集合任取两个元素构成子集的样本空间．
【答案】
【解析】从集合任取两个元素，
则构成子集的样本空间为.
【例2-2】（2023·高一课时练习）袋中放有4个白球、2个黑球，写出“从中取出2个球”的等可能的样本空间．
【答案】
【解析】用表示4个白球，用表示2个黑球，
故“从中取出2个球”的等可能的样本空间为：．
【例2-3】（2022春·广东揭阳·高一校考阶段练习）有两颗正四面体的玩具，其四个面上分别标有数字1，2，3，4，下面做投掷这两颗正四面体玩具的试验：用表示结果，其中表示第1颗正四面体玩具出现的点数，表示第2颗正四面体玩具出现的点数.试写出：（以下各小题先回答基本事件数目，再具体作答）
(1)试验的基本事件；
(2)事件“出现点数之和大于3”包含的基本事件；
(3)事件“出现点数相等”包含的基本事件.
【答案】(1)16个，答案见解析；
(2)13个，答案见解析；
(3)4个，答案见解析.
【解析】（1）这个试验的基本事件一共有个，分别为：
，，，，，，，，
，，，，，，，.
（2）事件“出现点数之和大于3”包含以下个基本事件：
，，，，，，，，
，，，，.
（3）事件“出现点数相等”包含以下个基本事件：，，，.
题型三 事件的关系
【例3-1】（2023吉林长春）盒子中装有红色，黄色和黑色小球各2个，一次取出2个小球，下列事件中，与事件“2个小球都是红色”对立的事件是（ ）
A．2个小球都是黑色B．2个小球恰有1个是红色
C．2个小球都不是红色D．2个小球至多有1个是红色
【答案】D
【解析】对于A，“2个小球都是黑色”与“2个小球都是红色”是只互斥不对立事件，故A不正确；
对于B，“2个小球恰有1个是红色” 与“2个小球都是红色”是只互斥不对立事件，故B不正确；
对于C，“2个小球都不是红色” 与“2个小球都是红色”是只互斥不对立事件，故C不正确；
对于D，“2个小球至多有1个是红色” 与“2个小球都是红色”是对立事件，故D正确.
故选：D
【例3-2】（2022上海）已知事件A､B､C满足，，则下列说法不正确的是（ ）
A．事件A发生一定导致事件C发生B．事件B发生一定导致事件C发生
C．事件发生不一定导致事件发生D．事件发生不一定导致事件发生
【答案】D
【解析】因为事件A､B､C满足，，所以，所以A正确；
事件B发生一定导致事件C发生，B正确；
因为，所以，所以事件发生不一定导致事件发生，所以C正确；
因为，所以，事件发生一定导致事件发生，所以D错误.
故选：D.
题型四 事件的运算
【例4-1】（2022·全国·高一专题练习）抛掷一枚骰子，“向上的面的点数是1或2”为事件，“向上的面的点数是2或3”为事件，则（ ）
A．B．
C．表示向上的面的点数是1或2或3D．表示向上的面的点数是1或2或3
【答案】C
【解析】由题意可知，，，，，所以，，2，，
则表示向上的面的点数是1或2或3，故ABD错误，C正确．故选：C．
【例4-2】（2022·高一单元测试）某小组有3名男生和2名女生，从中任选2名参加演讲比赛，设={2名全是男生}，{2名全是女生}，{恰有一名男生}，{至少有一名男生}，则下列关系不正确的是（ ）
A．B．C．D．
【答案】D
【解析】至少有1名男生包含2名全是男生､1名男生1名女生，故，，
故A，C正确；
事件B与D是互斥事件，故，故B正确，
表示的是2名全是男生或2名全是女生，表示2名全是女生或名至少有一名男生，
故，D错误，故选：D.
题型五 古典概型的判断
【例5-1】（2022·高一单元测试）以下试验不是古典概型的有（ ）
A．从6名同学中，选出4名参加学校文艺汇演，每个人被选中的可能性大小
B．同时掷两枚骰子，点数和为7的概率
C．近三天中有一天降雪的概率
D．3个人站成一排，其中甲，乙相邻的概率
【答案】C
【解析】A选项，从6名同学中，选出4名参加学校文艺汇演，每个人被选中的可能性相等，满足有限性和等可能性，是古典概型；
B选项中，同时同时掷两枚骰子，点数和为7的事件是不可能事件，有限性和等可能性，是古典概型；
C选项中，不满足等可能性，不是古典概型；
D选项中，3个人站成一排，其中甲，乙相邻的概率，满足有限性和等可能性，是古典概型．
故选：C．
【例5-2】（2022·高一课时练习）下列试验是古典概型的是（ ）
A．在平面直角坐标系内，从横坐标和纵坐标都是整数的所有点中任取一点
B．某射手射击一次，可能命中0环，1环，2环，…，10环
C．某小组有男生5人，女生3人，从中任选1人做演讲
D．在适宜的条件下，种下一粒种子，观察它是否发芽
【答案】C
【解析】对于A，横坐标和纵坐标都是整数的点有无限多个，不满足有限样本空间特征，故该选项错误；
对于B，命中0环，1环，2环…，10环的概率不相同，不满足等可能性特征，故该选项错误；
对于C，人数有限，且任选1人与学生的性别无关，是等可能的，故该选项正确；
对于D，“发芽”与“不发芽”的概率不一定相等，不满足等可能性特征，故该选项错误；
故选：C.
题型六 古典概型的样本空间
【例6-1】（2023·陕西铜川）某活动小组由2名男同学与3名女同学组成，他们完成一项活动后，要从这5名同学中选2人写活动体会，则所选2人中没有男生的概率为（ ）
A．B．C．D．
【答案】B
【解析】设2名男生为，3名女生为，
从5人中选2人的总选法为，
共10种不同选法，
则没有男生的选法共3种：，
故所求概率为．
故选:B.
【例6-2】（2023·高一课时练习）从一个装有2黄2绿的袋子里，
(1)有放回的摸球两次,两次摸到的都是绿球的概率是多少？
(2)不放回的摸球两次,两次摸到的都是绿球的概率是多少？
【答案】(1)
(2)
【解析】（1）对有放回的摸球，第一次摸出绿球的概率，第二次摸出绿球的概率，故两次摸到的都是绿球的概率是.
（2）对不放回的摸球，所有可能的结果共有种，两次都摸到绿球的结果有种，根据古典概型概率的求法，不放回的摸球两次摸到的都是绿球的概率为.
题型七 概率的性质
【例7-1】（2022·全国·高一期末）甲、乙两位同学进行羽毛球比赛，约定五局三胜制（无平局），已知甲每局获胜的概率都为，且前两局以领先，则最后甲获胜的概率为（ ）
A．B．C．D．
【答案】D
【解析】最后甲获胜含3种情况：①第三局甲胜，概率为；
②第三局乙胜，第四局甲胜，概率为；
③第三局和第四局乙胜，第五局甲胜，概率为．
所以最后甲获胜的概率为．
故选：D
【例7-2】（2023·全国·高一专题练习）已知，，如果，那么（ ）
A．0.7B．0.6C．0.4D．0.3
【答案】A
【解析】∵，∴，互斥，∴.故选：A.
【例7-3】．（2022·全国·高三专题练习）已知随机事件，，中，与互斥，与对立，且，，则（ ）
A．0.3B．0.6C．0.7D．0.8
【答案】C
【解析】因为，事件与对立，所以，又，与互斥，
所以.
故选：C.
【例7-4】（2022·高一课时练习）班级新年晚会设置抽奖环节．不透明纸箱中有大小、质地相同的红球3个(编号为1，2，3)，黄球2个(编号为4，5)，有如下两种方案可供选择：
方案一：一次性抽取2个球，若颜色相同，则获得奖品；
方案二：依次无放回地抽取2个球，若颜色相同，则获得奖品；
方案三：依次有放回地抽取2个球，若编号的数字之和大于5，则获得奖品．
(1)分别写出按方案一和方案二抽奖的所有样本点；
(2)哪种方案获得奖品的可能性更大？并说明理由．
【答案】(1)答案见解析；
(2)方案三获得奖品的可能性更大，理由见解析
【解析】（1）
记摸到1，2，3号红球分别为，，，摸到4，5号黄球分别为，，
则按方案一一次性抽取2个球的所有样本点为，，，，，，，，，，共10个；
按方案二依次无放回地抽取2个球的所有样本点为，，，，，，，，，，，，，，，，，，，，共20个；
（2）
方案一中，设事件A表示“一次性抽取的2个球颜色相同”，
则由（1）知事件A包含，，，，共4个样本点，
故；
方案二中，设事件B表示“依次无放回抽取的2个球颜色相同”，
则由（1）知事件B包含，，，，，，，，共8个样本点，
故；
方案三中，设两次抽查取的球所标的数字分别为、，
则所有可能的基本事件对应的二元有序数组表示如下表，共25个基本事件，
在方案三中，设事件C表示“抽取的2个球编号的数字之和大于5”，
则事件C包含(1，5)，(2，4)，(2，5)，(3，3)，(3，4)，(3，5)，(4，2)，(4，3)，(4，4)，(4，5)，(5，1)，(5，2)，(5，3)，(5，4)，(5，5)，共15个样本点，
故；
因为，所以选择方案三获得奖品的可能性更大
定义
符号
图示
包含关系
一般地，若事件A发生，则事件B一定发生，称事件B包含事件A(或事件A包含于事件B)
B⊇A(或A⊆B)
相等关系
如果事件B包含事件A，事件A也包含事件B，即B⊇A且A⊇B，则称事件A与事件B相等
A＝B
互斥事件
一般地，如果事件A与事件B不能同时发生，也就是说A∩B是一个不可能事件，即A∩B＝∅，则称事件A与事件B互斥(或互不相容)
A∩B＝∅
对立事件
一般地，如果事件A和事件B在任何一次试验中有且仅有一个发生，即A∪B＝Ω，且A∩B＝∅，那么称事件A与事件B互为对立，事件A的对立事件记为eq \x\t(A)
A∪B＝Ω
A∩B＝∅
定义
符号
图示
并事件
(或和事件)
一般地，事件A与事件B至少有一个发生，这样的一个事件中的样本点或者在事件A中，或者在事件B中，我们称这个事件为事件A与事件B的并事件(或和事件)
A∪B
(或A＋B)
交事件
(或积事件)
一般地，事件A与事件B同时发生，这样的一个事件中的样本点既在事件A中，也在事件B中，我们称这样的一个事件为事件A与事件B的交事件(或积事件)
A∩B
(或AB)
（1，1）
（1，2）
（1，3）
（1，4）
（1，5）
（2，1）
（2，2）
（2，3）
（2，4）
（2，5）
（3，1）
（3，2）
（3，3）
（3，4）
（3，5）
（4，1）
（4，2）
（4，3）
（4，4）
（4，5）
（5，1）
（5，2）
（5，3）
（5，4）
（5，5）