
高中数学人教A版 (2019)必修 第二册10.1 随机事件与概率当堂达标检测题
展开典例精讲
考点一 随机事件的判断
【例1】(2021秋·陕西榆林·高二陕西省神木中学校考阶段练习)下列事件中,随机事件的个数是( )
①未来某年8月18日,北京市不下雨;
②在标准大气压下,水在4℃时结冰;
③从标有1,2,3,4的4张号签中任取一张,恰好取到1号签;
④任取,则.
A.1B.2C.3D.4
【一隅三反】
1.(2023·高一课时练习)下列四个事件:
①明天上海的天气有时有雨;②东边日出西边日落;③鸡蛋里挑骨头;④守株待兔.
其中必然事件有( )
A.0个B.1个C.2个D.3个
2(2023·高一课时练习)下列事件中,属于随机现象的序号是______.
①明天是阴天; ②方程有两个不相等的实数根;
③明天吴淞口的最高水位是4.5米; ④三角形中,大角对大边.
3.(2023·高一单元测试)下列事件:
①空间任意三点可以确定一个平面;
②367个人中至少有两个人的生日在同一天;
③6个人的生日在不同月份;
④掷两次骰子,点数和不小于2;
⑤两条异面直线所成角为钝角.
其中,______是不确定事件,______是必然事件,______是不可能事件(填写序号).
4.(2022秋·安徽马鞍山)在100件产品中,有95件一级品,5件二级品,给出下列事件:
①在这100件产品中任意选出6件,全部是一级品;
②在这100件产品中任意选出6件,全部是二级品;
③在这100件产品中任意选出6件,不全是一级品;
④在这100件产品中任意选出6件,至少一件是一级品,
其中__________是随机事件.(如果没有,请填“无”;如果有,请填序号)
考点二 有限样本空间
【例2】(2022·高一课时练习)一个口袋内装有除颜色外完全相同的5个球,其中3个白球,2个黑球,从中一次摸出2个球.
(1)写出这个试验的样本空间;
(2)写出“2个球都是白球”这一事件所对应的子集.
【一隅三反】
1.(2022秋·山东济宁)做抛掷红、蓝两枚骰子的试验,用表示结果,其中表示红色骰子出现的点数,表示蓝色骰子出现的点数.写出:
(1)这个试验的样本空间;
(2)这个试验的结果的个数;
(3)指出事件的含义.
2.(2022·课时练习)先后两次掷一枚均匀的骰子,观察朝上的面的点数.
(1)写出对应的样本空间;
(2)用集合表示事件A:点数之和为3;事件B:点数之和不超过4.
3.(2022·高一课时练习)已知集合,,从两个集合中各取一个元素构成点的坐标.
(1)写出这个试验的样本空间;
(2)求这个试验样本点的总数;
(3)写出“得到的点是第一象限内的点”这一事件所包含的样本点;
(4)说出事件所表示的实际意义.
考点三 事件的关系与运算
【例3-1】(2022秋·陕西榆林)某人射击一次,设事件A:“击中环数小于8”;事件B:“击中环数大于8”;事件C:“击中环数不小于8”,事件D:“击中环数不大于9”,则下列关系正确的是( )
A.A和B为对立事件B.B和C为互斥事件
C.A和C为对立事件D.B与D为互斥事件
【例3-2】(2022春·北京通州·高一统考期末)抛掷一颗质地均匀的骰子,有如下随机事件:“点数不大于3”,“点数大于3”,“点数大于5”;“点数为奇数”;“点数为i”,其中.下列结论正确的是( )
A.B.C.与互斥D.与互为对立
【一隅三反】
1.(2022·高一课时练习)在试验E“从1,2,3,4这4个数中,任取2个数求和”中,事件A表示“这2个数的和大于4”,事件B表示“这2个数的和为偶数”,则和中包含的样本点数分别为( )
A.1,6B.4,2C.5,1D.6,1
2.(2022上海徐汇)设M,N为两个随机事件,如果M,N为互斥事件,那么( )
A.是必然事件B.是必然事件
C.与一定为互斥事件D.与一定不为互斥事件
考点四 古典概型
【例4-1】(2022·高一课时练习)下列不是古典概型的是( )
A.在6个完全相同的小球中任取1个
B.任意抛掷两颗骰子,所得点数之和作为样本点
C.已知袋子中装有大小完全相同的红色、绿色、黑色小球各1个,从中任意取出1个球,观察球的颜色
D.从南京到北京共有n条长短不同的路线,求某人正好选中最短路线的概率
【例4-2】(2023·陕西西安)12月4日20时09分,神舟十四号载人飞船返回舱在东风着陆场成功着陆,神舟十四号载人飞行任务取得圆满成功.经历了120天全生命周期的水稻和拟南芥种子,也一起搭乘飞船返回舱从太空归来.我国在国际上首次完成水稻“从种子到种子”全生命周期空间培养实验,在此之前国际上在空间只完成了拟南芥、油菜、豌豆和小麦“从种子到种子”的培养.若从水稻、拟南芥、油菜、豌豆和小麦这5种种子中随机选取2种,则水稻种子被选中的概率为( )
A.B.C.D.
【一隅三反】
1.(2022·高一课前预习)下列概率模型中,是古典概型的个数为( )
(1)从区间[1,10]内任取一个数,求取到1的概率;
(2)从1~10中任意取一个整数,求取到1的概率;
(3)在一个正方形ABCD内画一点P,求P刚好与点A重合的概率;
(4)向上抛掷一枚不均匀的硬币,求出现反面朝上的概率.
A.1B.2C.3D.4
2.(2023春·江西)袋中装有四个大小完全相同的小球,分别写有“中、华、道、都”四个字,每次有放回地从中任取一个小球,直到写有“道”、“都”两个字的小球都被取到,则停止取球.现用随机模拟的方法估计取球停止时的概率,具体方法是:利用计算机产生0到3之间取整数值的随机数,用0,1,2,3分别代表“中、华、道、都”四个字,以每三个随机数为一组,表示取球三次的结果.现经随机模拟产生了以下18组随机数:
232 321 230 023 231 021 122 203 012
231 130 133 231 031 123 122 103 233
由此可以估计,恰好取球三次就停止的概率为( )
A.B.C.D.
3.(2023贵州六盘水)当前疫情防控形势依然复杂严峻,为进一步增强学生的防控意识,某校让全体学生充分了解疫情的防护知识,提高防护能力,做到科学防护,组织学生进行了疫情防控科普知识线上问答,共有100人参加了这次问答,将他们的成绩(满分100分)分成五组依次为,,,,,制成如图所示的频率分布直方图.
(1)求图中的值;
(2)试估计这100人的问答成绩的众数和平均数;
(3)采用按比例分配的分层抽样的方法,从问答成绩在内的学生中随机抽取13人作为疫情防控知识宣讲使者,再从第四组和第五组的使者中随机抽取2人作为组长,求这2人来自不同组的概率.
考点五 概率的性质
【例5-1】(2022春·上海黄浦·高一上海外国语大学附属大境中学校考期末)已知事件A与事件B是互斥事件,则( )
A.B.
C.D.
【例5-2】(2023春·安徽·高一合肥市第八中学校联考开学考试)若事件为两个互斥事件,且,有以下四个结论,其中正确的结论是( )
①
②
③
④
A.①③④B.②③④C.①②④D.①②③
【一隅三反】
1.(2023四川南充)设A,B是同一试验中的两个随机事件,与分别是事件,事件发生的概率,若,,则“”是“事件A,B为对立事件”的( )条件
A.充分不必要B.必要不充分
C.充要D.既不充分也不必要
2.(2023·全国·高一专题练习)袋子中有5个质地完全相同的球,其中2个白球,3个是红球,从中不放回地依次随机摸出两个球,记第一次摸到红球”,“第二次摸到红球”,则以下说法正确的是( )
A.B.
C.D.
3.(2022春·陕西咸阳·高一校考期中)保险柜的密码由0,1,2,3,4,5,6,7,8,9中的四个数字组成,假设一个人记不清自己的保险柜密码,只记得密码全部由奇数组成且按照递增顺序排列,则最多输入2次就能开锁的概率是( )
A.B.C.D.
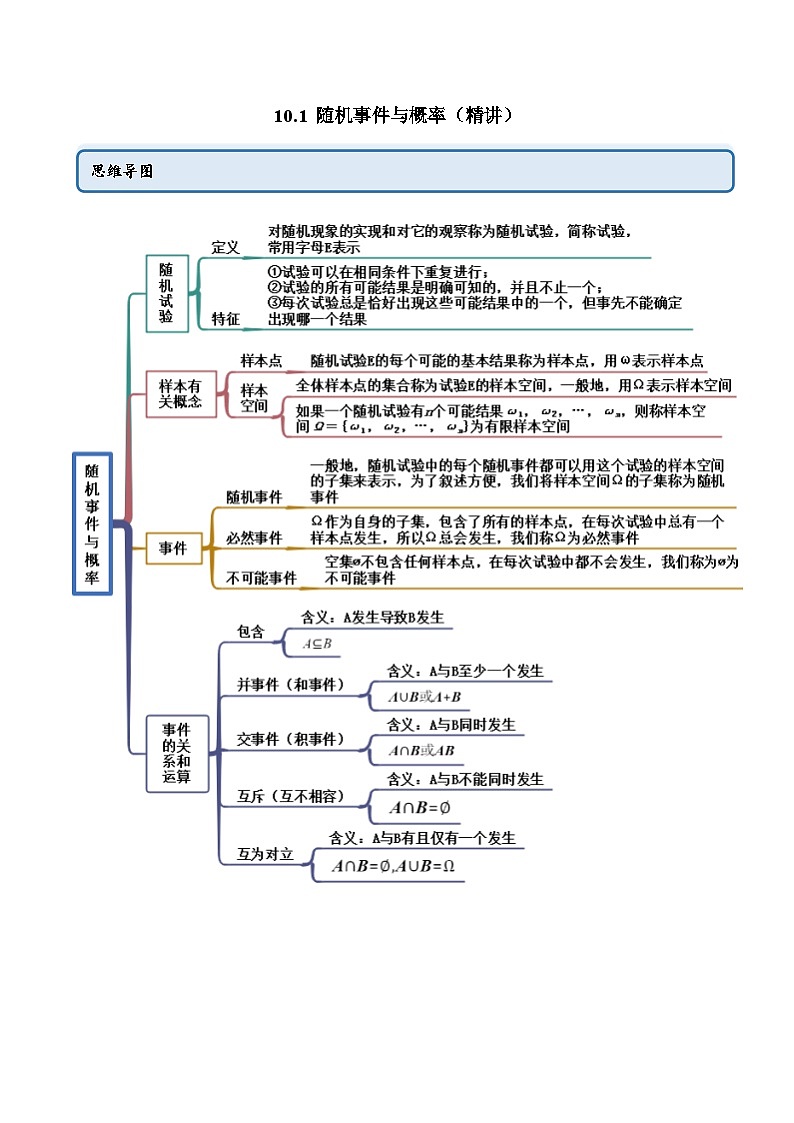
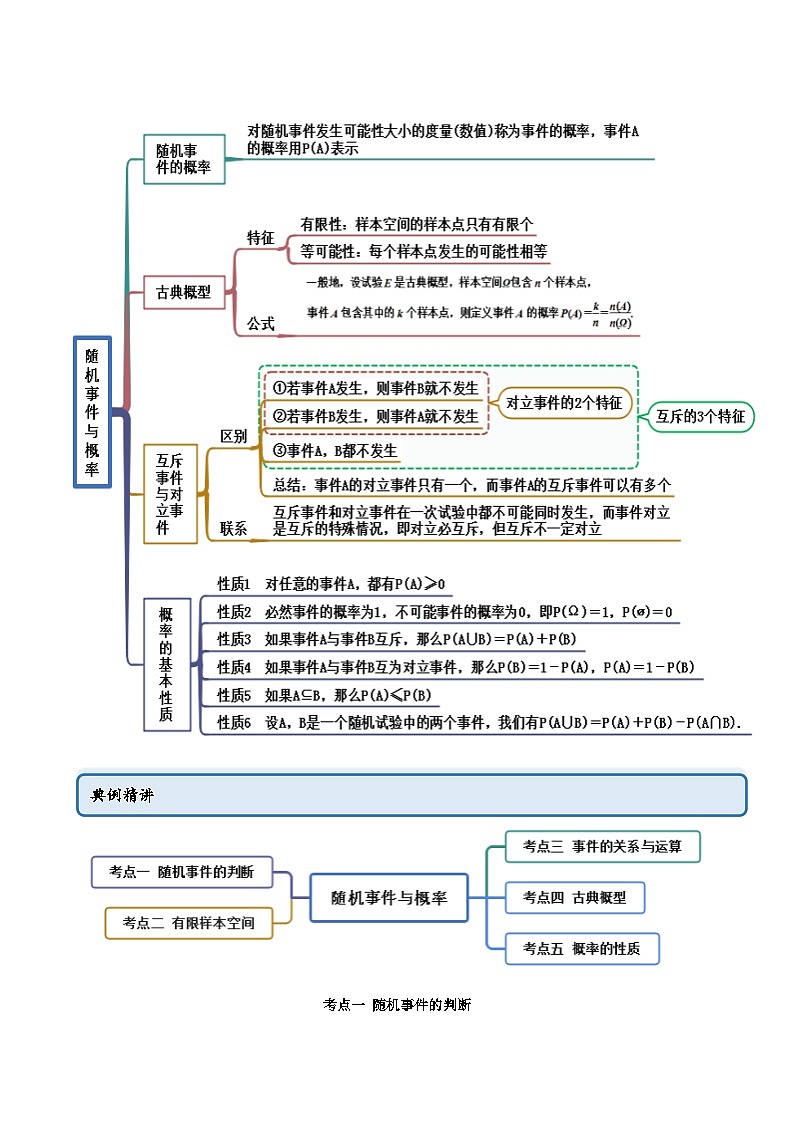
10.1 随机事件与概率(精讲)思维导图
典例精讲
考点一 随机事件的判断
【例1】(2021秋·陕西榆林·高二陕西省神木中学校考阶段练习)下列事件中,随机事件的个数是( )
①未来某年8月18日,北京市不下雨;
②在标准大气压下,水在4℃时结冰;
③从标有1,2,3,4的4张号签中任取一张,恰好取到1号签;
④任取,则.
A.1B.2C.3D.4
【答案】B
【解析】①未来某年8月18日,北京市不下雨,属于随机事件;
②在标准大气压下,水在4℃时结冰,属于不可能事件;
③从标有1,2,3,4的4张号签中任取一张,恰为1号签,属于随机事件;
④任取,则,属于必然事件;
所以属于随机事件的有①③,即随机事件的个数是.故选:B
【一隅三反】
1.(2023·高一课时练习)下列四个事件:
①明天上海的天气有时有雨;②东边日出西边日落;③鸡蛋里挑骨头;④守株待兔.
其中必然事件有( )
A.0个B.1个C.2个D.3个
【答案】B
【解析】由题意可知,①明天上海的天气有时有雨为随机事件;②东边日出西边日落为必然事件;
③鸡蛋里挑骨头为不可能事件;④守株待兔为随机事件,故必然事件有1个,故选:B
2(2023·高一课时练习)下列事件中,属于随机现象的序号是______.
①明天是阴天; ②方程有两个不相等的实数根;
③明天吴淞口的最高水位是4.5米; ④三角形中,大角对大边.
【答案】①③
【解析】对于①③,明天的事是未来才发生的事,具有不确定性,故①③属于随机现象;
对于②,由得,显然在实数域方程无解,故②属于不可能事件;
对于④,由正弦定理易知在三角形中,大角对大边.故④属于确定事件;
综上:属于随机现象的序号是①③.故答案为:①③.
3.(2023·高一单元测试)下列事件:
①空间任意三点可以确定一个平面;
②367个人中至少有两个人的生日在同一天;
③6个人的生日在不同月份;
④掷两次骰子,点数和不小于2;
⑤两条异面直线所成角为钝角.
其中,______是不确定事件,______是必然事件,______是不可能事件(填写序号).
【答案】 ①③ ②④ ⑤
【解析】因为空间中不共线的三点可以确定一个平面,所以事件①可能发生也可能不发生,故①是不确定事件;
因为每年有365天或366天,所以事件②一定发生,故②是必然事件;
事件③可能发生也可能不发生,故③是不确定事件;
因为掷两次骰子,点数和的可能结果是:2,3,…,12,所以事件④一定发生,故④是必然事件;
因为两条异面直线所成角的范围是(0°,90°],所以事件⑤不可能发生,故⑤是不可能事件.
故答案为:①③,②④,⑤.
4.(2022秋·安徽马鞍山)在100件产品中,有95件一级品,5件二级品,给出下列事件:
①在这100件产品中任意选出6件,全部是一级品;
②在这100件产品中任意选出6件,全部是二级品;
③在这100件产品中任意选出6件,不全是一级品;
④在这100件产品中任意选出6件,至少一件是一级品,
其中__________是随机事件.(如果没有,请填“无”;如果有,请填序号)
【答案】①③
【解析】对于①,因为100件产品中,有95件一级品,5件二级品,所以在这100件产品中任意选出6件,全部是一级品是椭机事件,
对于②,因为100件产品中,有95件一级品,5件二级品,所以在这100件产品中任意选出6件,全部是二级品是不可能事件,
对于③,因为100件产品中,有95件一级品,5件二级品,所以在这100件产品中任意选出6件,不全是一级品是随机事件,
对于④,因为100件产品中,有95件一级品,5件二级品,所以在这100件产品中任意选出6件,至少一件是一级品是必然事件,故答案为:①③.
考点二 有限样本空间
【例2】(2022·高一课时练习)一个口袋内装有除颜色外完全相同的5个球,其中3个白球,2个黑球,从中一次摸出2个球.
(1)写出这个试验的样本空间;
(2)写出“2个球都是白球”这一事件所对应的子集.
【答案】(1)答案见解析;(2)答案见解析.
【解析】(1)分别记白球为1,2,3号,黑球为4,5号,则这个试验的样本空间为Ω={(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)}.[其中(1,2)表示摸到1号球和2号球]
(2)“2个球都是白球”这一事件就是子集{(1,2),(1,3),(2,3)}.
【一隅三反】
1.(2022秋·山东济宁)做抛掷红、蓝两枚骰子的试验,用表示结果,其中表示红色骰子出现的点数,表示蓝色骰子出现的点数.写出:
(1)这个试验的样本空间;
(2)这个试验的结果的个数;
(3)指出事件的含义.
【答案】(1)答案见解析(2)(3)抛掷红、蓝两枚骰子,掷出的点数之和为
【解析】(1)样本空.
(2)由(1)知:这个试验的结果的个数共有个.
(3)由可知:事件表示抛掷红、蓝两枚骰子,掷出的点数之和为.
2.(2022·课时练习)先后两次掷一枚均匀的骰子,观察朝上的面的点数.
(1)写出对应的样本空间;
(2)用集合表示事件A:点数之和为3;事件B:点数之和不超过4.
【答案】(1)Ω,;
(2),.
【解析】(1)用表示第一次掷出1点,第二次掷出2点,其他的样本点用类似的方法表示,则可知所有样本点均可表示成的形式,其中都是中的数.
因此,样本空间Ω,;
(2)根据题意,,.
3.(2022·高一课时练习)已知集合,,从两个集合中各取一个元素构成点的坐标.
(1)写出这个试验的样本空间;
(2)求这个试验样本点的总数;
(3)写出“得到的点是第一象限内的点”这一事件所包含的样本点;
(4)说出事件所表示的实际意义.
【答案】(1)答案见解析;
(2)
(3)
(4)得到的点是第三象限内的点.
【解析】(1)样本空间为:
(2)由知这个试验样本点的总数为.
(3)得到的点是第一象限内的点”这一事件所包含的样本点为.
(4)事件表示得到的点是第三象限内的点.
考点三 事件的关系与运算
【例3-1】(2022秋·陕西榆林)某人射击一次,设事件A:“击中环数小于8”;事件B:“击中环数大于8”;事件C:“击中环数不小于8”,事件D:“击中环数不大于9”,则下列关系正确的是( )
A.A和B为对立事件B.B和C为互斥事件
C.A和C为对立事件D.B与D为互斥事件
【答案】C
【解析】由题意可知:设事件A:“击中环数小于8”与事件B:“击中环数大于8”是互斥事件但不是对立事件,故A选项错误;
事件B:“击中环数大于8” 与事件C:“击中环数不小于8”,能同时发生,所以不是互斥事件,故B选项错误;
事件A:“击中环数小于8”与事件C:“击中环数不小于8”是对立事件,故C选项正确;
事件B:“击中环数大于8”与事件D:“击中环数不大于9”能同时发生,不是互斥事件,故D选项错误.
故选:C.
【例3-2】(2022春·北京通州·高一统考期末)抛掷一颗质地均匀的骰子,有如下随机事件:“点数不大于3”,“点数大于3”,“点数大于5”;“点数为奇数”;“点数为i”,其中.下列结论正确的是( )
A.B.C.与互斥D.与互为对立
【答案】B
【解析】因事件含有“点数为2”的基本事件,而事件不含这个基本事件,A不正确;
事件含有3个基本事件:“点数为1”,“点数为3”, “点数为5”,即,B正确;
事件与都含有“点数为6”的基本事件, 与不互斥,C不正确;
事件与不能同时发生,但可以同时不发生,与不对立,D不正确.
故选:B
【一隅三反】
1.(2022·高一课时练习)在试验E“从1,2,3,4这4个数中,任取2个数求和”中,事件A表示“这2个数的和大于4”,事件B表示“这2个数的和为偶数”,则和中包含的样本点数分别为( )
A.1,6B.4,2C.5,1D.6,1
【答案】C
【解析】试验E的样本空间为Ω={(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}.
其中事件A中所含的样本点为(1,4),(2,3),(2,4),(3,4),共4个;
事件B中所含的样本点为(1,3),(2,4),共2个.
所以事件中所含的样本点为(1,3),(1,4),(2,3),(2,4),(3,4),共5个;
事件中所含的样本点为(2,4),共1个.
故选:C.
2.(2022上海徐汇)设M,N为两个随机事件,如果M,N为互斥事件,那么( )
A.是必然事件B.是必然事件
C.与一定为互斥事件D.与一定不为互斥事件
【答案】A
【解析】因为M,N为互斥事件,则有以下两种情况,如图所示
(第一种情况)
(第二种情况)
无论哪种情况,均是必然事件.故A正确.如果是第一种情况,不是必然事件,故B不正确,如果是第一种情况,与不一定为互斥事件,故C不正确,如果是第二种情况,与一定为互斥事件,故D不正确.故选:A.
考点四 古典概型
【例4-1】(2022·高一课时练习)下列不是古典概型的是( )
A.在6个完全相同的小球中任取1个
B.任意抛掷两颗骰子,所得点数之和作为样本点
C.已知袋子中装有大小完全相同的红色、绿色、黑色小球各1个,从中任意取出1个球,观察球的颜色
D.从南京到北京共有n条长短不同的路线,求某人正好选中最短路线的概率
【答案】B
【解析】选项A中,在6个完全相同的小球中任取1个,每个球被抽到的机会均等,且该试验包含的基本事件其有6个,故A符合古典概型;
选项B中,由于点数的和出现的可能性不相等,故B不是古典概型;
选项C中,该试验满足古典概型的有限性和等可能性,故C是古典概型;
选项D中,满足古典概型的有限性和等可能性,故D是古典概型.
故选:B
【例4-2】(2023·陕西西安)12月4日20时09分,神舟十四号载人飞船返回舱在东风着陆场成功着陆,神舟十四号载人飞行任务取得圆满成功.经历了120天全生命周期的水稻和拟南芥种子,也一起搭乘飞船返回舱从太空归来.我国在国际上首次完成水稻“从种子到种子”全生命周期空间培养实验,在此之前国际上在空间只完成了拟南芥、油菜、豌豆和小麦“从种子到种子”的培养.若从水稻、拟南芥、油菜、豌豆和小麦这5种种子中随机选取2种,则水稻种子被选中的概率为( )
A.B.C.D.
【答案】D
【解析】设水稻、拟南芥、油菜、豌豆和小麦分别为,
则共有:10种情况,
满足条件的有4种情况,则.
故选:D
【一隅三反】
1.(2022·高一课前预习)下列概率模型中,是古典概型的个数为( )
(1)从区间[1,10]内任取一个数,求取到1的概率;
(2)从1~10中任意取一个整数,求取到1的概率;
(3)在一个正方形ABCD内画一点P,求P刚好与点A重合的概率;
(4)向上抛掷一枚不均匀的硬币,求出现反面朝上的概率.
A.1B.2C.3D.4
【答案】A
【解析】第1个概率模型不是古典概型,因为从区间[1,10]内任意取出一个数,有无数个对象可取,所以不满足“有限性”.
第2个概率模型是古典概型,因为试验结果只有10个,而且每个数被抽到的可能性相等,即满足有限性和等可能性;
第3个概率模型不是古典概型,在一个正方形ABCD内画一点P,有无数个点,不满足“有限性”;
第4个概率模型也不是古典概型,因为硬币不均匀,因此两面出现的可能性不相等.
故选:A.
2.(2023春·江西)袋中装有四个大小完全相同的小球,分别写有“中、华、道、都”四个字,每次有放回地从中任取一个小球,直到写有“道”、“都”两个字的小球都被取到,则停止取球.现用随机模拟的方法估计取球停止时的概率,具体方法是:利用计算机产生0到3之间取整数值的随机数,用0,1,2,3分别代表“中、华、道、都”四个字,以每三个随机数为一组,表示取球三次的结果.现经随机模拟产生了以下18组随机数:
232 321 230 023 231 021 122 203 012
231 130 133 231 031 123 122 103 233
由此可以估计,恰好取球三次就停止的概率为( )
A.B.C.D.
【答案】C
【解析】根据题意可知,所有事件的结果数有18种,
其中满足恰好取球三次时“道”、“都”两个字的小球都被取到的事件有:023,203,123共3种,
记“恰好取球三次就停止”为事件,所以.
故答案为:C
3.(2023贵州六盘水)当前疫情防控形势依然复杂严峻,为进一步增强学生的防控意识,某校让全体学生充分了解疫情的防护知识,提高防护能力,做到科学防护,组织学生进行了疫情防控科普知识线上问答,共有100人参加了这次问答,将他们的成绩(满分100分)分成五组依次为,,,,,制成如图所示的频率分布直方图.
(1)求图中的值;
(2)试估计这100人的问答成绩的众数和平均数;
(3)采用按比例分配的分层抽样的方法,从问答成绩在内的学生中随机抽取13人作为疫情防控知识宣讲使者,再从第四组和第五组的使者中随机抽取2人作为组长,求这2人来自不同组的概率.
【答案】(1)
(2)75,73.5
(3)
【解析】(1)依题意可得:,解得:;
(2)根据频率分布直方图知:众数的估计值为,
平均数的估计值为,
所以这100人的问答成绩的众数与平均数的估计值分别为75,73.5..
(3)由题可知,在问答成绩,,三组中,人数之比为7:5:1,
现采用分层抽样从中抽取13人,所以三组中每组各抽学生人数分别为7,5,1.
分别记中所抽取的5人编号依次为1,2,3,4,5.
中所抽取的1人编号为.
所以从6人中随机抽取2人的样本空间为:,,
,共15个样本点.
其中这2人来自不同组(记为事件)的样本点有5个,所以.
所以这2人来自不同组的概率为.
考点五 概率的性质
【例5-1】(2022春·上海黄浦·高一上海外国语大学附属大境中学校考期末)已知事件A与事件B是互斥事件,则( )
A.B.
C.D.
【答案】D
【解析】因为事件A与事件B是互斥事件,不一定是互斥事件,所以不一定为0,故A错误;
因为,所以,而不一定为0,故B错误;
因为事件A与事件B是互斥事件,不一定是对立事件,所以C错误;
因为事件A与事件B是互斥事件,是必然事件, 所以,故D正确.
故选:D.
【例5-2】(2023春·安徽·高一合肥市第八中学校联考开学考试)若事件为两个互斥事件,且,有以下四个结论,其中正确的结论是( )
①
②
③
④
A.①③④B.②③④C.①②④D.①②③
【答案】A
【解析】事件为两个互斥事件,,,故①正确;
事件为两个互斥事件,则,,故②错误;
,故③正确;
,故④正确,
综上,①③④正确,
故选:A.
【一隅三反】
1.(2023四川南充)设A,B是同一试验中的两个随机事件,与分别是事件,事件发生的概率,若,,则“”是“事件A,B为对立事件”的( )条件
A.充分不必要B.必要不充分
C.充要D.既不充分也不必要
【答案】B
【解析】因为,,若事件A,B为对立事件,则;
但推不出两个事件,对立;如掷一颗骰子,事件为出现1点,2点,3点;事件为出现3点,4点,5点,此时,但两个事件不对立,
所以“”是“事件A,B为对立事件”的必要不充分条件.
故选:B.
2.(2023·全国·高一专题练习)袋子中有5个质地完全相同的球,其中2个白球,3个是红球,从中不放回地依次随机摸出两个球,记第一次摸到红球”,“第二次摸到红球”,则以下说法正确的是( )
A.B.
C.D.
【答案】C
【解析】,则,故C正确;
,则,故A错误;
,则,故B错误;
,故D错误,
故选:C.
3.(2022春·陕西咸阳·高一校考期中)保险柜的密码由0,1,2,3,4,5,6,7,8,9中的四个数字组成,假设一个人记不清自己的保险柜密码,只记得密码全部由奇数组成且按照递增顺序排列,则最多输入2次就能开锁的概率是( )
A.B.C.D.
【答案】C
【解析】密码全部由奇数组成且按照递增顺序排列的结果有:,,共5个,它们等可能,
最多输入2次就能开锁的事件A,它是输入1次能开锁的事件,第2次输入才能开锁的事件的和,它们互斥,
,,则,
最多输入2次就能开锁的概率是.
故选:C
高中数学人教A版 (2019)必修 第二册10.3 频率与概率达标测试: 这是一份高中数学人教A版 (2019)必修 第二册<a href="/sx/tb_c4000316_t7/?tag_id=28" target="_blank">10.3 频率与概率达标测试</a>,共18页。试卷主要包含了频率与概率概念的辨析,频率与概率的计算,随机模拟,综合运用等内容,欢迎下载使用。
高中人教A版 (2019)第十章 概率10.1 随机事件与概率达标测试: 这是一份高中人教A版 (2019)<a href="/sx/tb_c4000314_t7/?tag_id=28" target="_blank">第十章 概率10.1 随机事件与概率达标测试</a>,共53页。
人教A版 (2019)必修 第二册9.2 用样本估计总体课后作业题: 这是一份人教A版 (2019)必修 第二册<a href="/sx/tb_c4000310_t7/?tag_id=28" target="_blank">9.2 用样本估计总体课后作业题</a>,共34页。试卷主要包含了总体取值规律的估计,统计图的解读,总体百分位数的估计,总体集中趋势的估计,总体离散程度的估计等内容,欢迎下载使用。













