高三数学一轮复习第二章函数第三课时函数的奇偶性、周期性与对称性课件

这是一份高三数学一轮复习第二章函数第三课时函数的奇偶性、周期性与对称性课件，共27页。PPT课件主要包含了考点一函数的奇偶性，最小正数等内容，欢迎下载使用。

提醒：定义域关于原点对称，这是函数具有奇偶性的必要不充分条件，所以首先考虑函数定义域．
f (－x)＝f (x)
f (－x)＝－f (x)
A　　　 　　　B
C　　　 　　　D
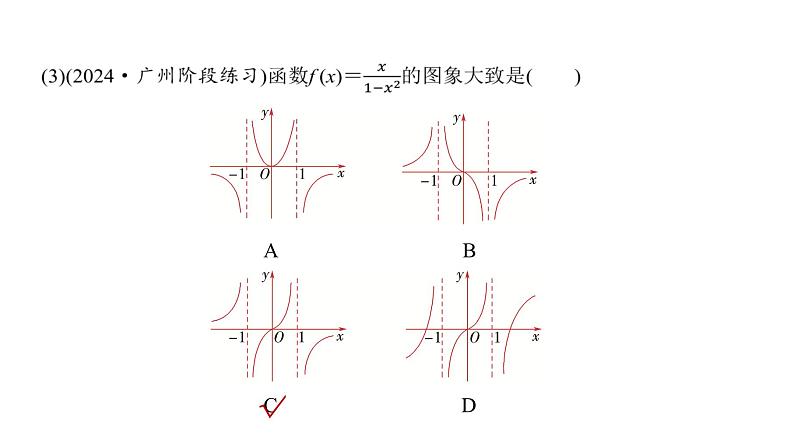
点拨　 本例(1)判断函数的奇偶性，首先考虑函数f (x)的定义域是否关于原点对称，其次再根据f (－x)与f (x)关系来判断；本例(2)借助偶函数f (x)＝f (－x)来解决；本例(3)中，在考虑函数的定义域、值域和奇偶性等函数的性质的前提下，还应考虑函数的特殊值，利用排除法选出正确选项．
A　　　　　　　　　 　　B
C　　　　　　　　　 　　D
考点二　函数的周期性1．周期函数：一般地，设函数f (x)的定义域为D，如果存在一个非零常数T，使得对每一个x∈D都有x＋T∈D，且____________，那么函数y＝f (x)就叫做周期函数，非零常数T叫做这个函数的周期．2．最小正周期：如果在周期函数f (x)的所有周期中存在一个____的正数，那么这个________就叫做f (x)的最小正周期．
f (x＋T)＝f (x)
点拨　本例(1)解决的关键是抓住f (x＋2)＝f (x)这个条件，一一验证即可；本例(2)根据f (x)是定义域为R的偶函数，所以f (x)＝f (－x)；再结合f (x)＝f (2－x)得出f (x)是周期为2的函数．
跟进训练2　已知f (x)是定义在R上的奇函数，∀x∈R，都有f (x＋4)＝f (x)，若当x∈[0，1]时，f (x)＝lg2(x＋a)，则f (－7)＝(　　)A．－1 B．0C．1 D．2
点拨　(1)函数y＝f (x)满足f (a＋x)＝f (a－x)(a>0)，若f (x)为奇函数，则其周期为T＝4a．若f (x)为偶函数，则其周期为T＝2a．(2)函数y＝f (x)(x∈R)的图象关于直线x＝a和x＝b(a

相关课件

2025年高考数学一轮复习-2.3.1-函数的奇偶性、周期性与对称性【课件】： 这是一份2025年高考数学一轮复习-2.3.1-函数的奇偶性、周期性与对称性【课件】，共52页。PPT课件主要包含了必备知识自主排查，核心考点师生共研，函数的奇偶性，函数的周期性，最小正周期，练一练，函数图象的对称性，用一用，1定义法，2图象法等内容，欢迎下载使用。

2024版新教材高考数学全程一轮总复习第二章函数与基本初等函数第三节函数的奇偶性周期性与对称性课件： 这是一份2024版新教材高考数学全程一轮总复习第二章函数与基本初等函数第三节函数的奇偶性周期性与对称性课件，共60页。PPT课件主要包含了必备知识·夯实双基，关键能力·题型突破，f－x＝fx，最小的正数，最小正数，答案BC，答案D，答案BD，答案C，答案A等内容，欢迎下载使用。

2024版高考数学一轮复习教材基础练第二章函数及其性质第三节函数的奇偶性周期性及函数图象的对称性教学课件： 这是一份2024版高考数学一轮复习教材基础练第二章函数及其性质第三节函数的奇偶性周期性及函数图象的对称性教学课件，共39页。PPT课件主要包含了教材知识萃取，1定义法，2图象法，教材素材变式，方法技巧，归纳总结，函数的周期性，函数图象的对称性，条件变式，结论拓展等内容，欢迎下载使用。