新高考数学三轮冲刺小题必练12 基本初等函数（2份打包，原卷版+教师版）

这是一份新高考数学三轮冲刺小题必练12 基本初等函数（2份打包，原卷版+教师版），文件包含新高考数学三轮冲刺小题必练12基本初等函数原卷版doc、新高考数学三轮冲刺小题必练12基本初等函数教师版doc等2份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。

1．函数的单调性
（1）单调函数的定义
（2）单调区间的定义
如果函数 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上是增函数或减函数，那么就说函数 SKIPIF 1 < 0 在这一区间具有(严格的)单调性，区间 SKIPIF 1 < 0 叫做 SKIPIF 1 < 0 的单调区间．
2．函数的最值
3．函数单调性的常用结论
（1）对 SKIPIF 1 < 0 在D上是增函数；
SKIPIF 1 < 0 在D上是减函数．
（2）对勾函数 SKIPIF 1 < 0 的增区间为 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，减区间为 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ．
（3）在区间 SKIPIF 1 < 0 上，两个增函数的和仍是增函数，两个减函数的和仍是减函数．
（4）函数 SKIPIF 1 < 0 的单调性与函数 SKIPIF 1 < 0 和 SKIPIF 1 < 0 的单调性的关系是“同增异减”．
4．函数的奇偶性
5．周期性
（1）周期函数：对于函数 SKIPIF 1 < 0 ，如果存在一个非零常数 SKIPIF 1 < 0 ，使得当 SKIPIF 1 < 0 取定义域内的任何值时，都有 SKIPIF 1 < 0 ，那么就称函数 SKIPIF 1 < 0 为周期函数，称 SKIPIF 1 < 0 为这个函数的周期．
（2）最小正周期：如果在周期函数 SKIPIF 1 < 0 的所有周期中存在一个最小的正数，那么这个正数就叫做 SKIPIF 1 < 0 的最小正周期．
6．函数奇偶性常用结论
（1）如果函数 SKIPIF 1 < 0 是偶函数，那么 SKIPIF 1 < 0 ．
（2）奇函数在两个对称的区间上具有相同的单调性；偶函数在两个对称的区间上具有相反的单调性．
（3）在公共定义域内有：奇±奇＝奇，偶±偶＝偶，奇×奇＝偶，偶×偶＝偶，奇×偶＝奇．
7．函数周期性常用结论
对 SKIPIF 1 < 0 定义域内任一自变量的值 SKIPIF 1 < 0 ：
（1）若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ．
（2）若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ．
（3）若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ．
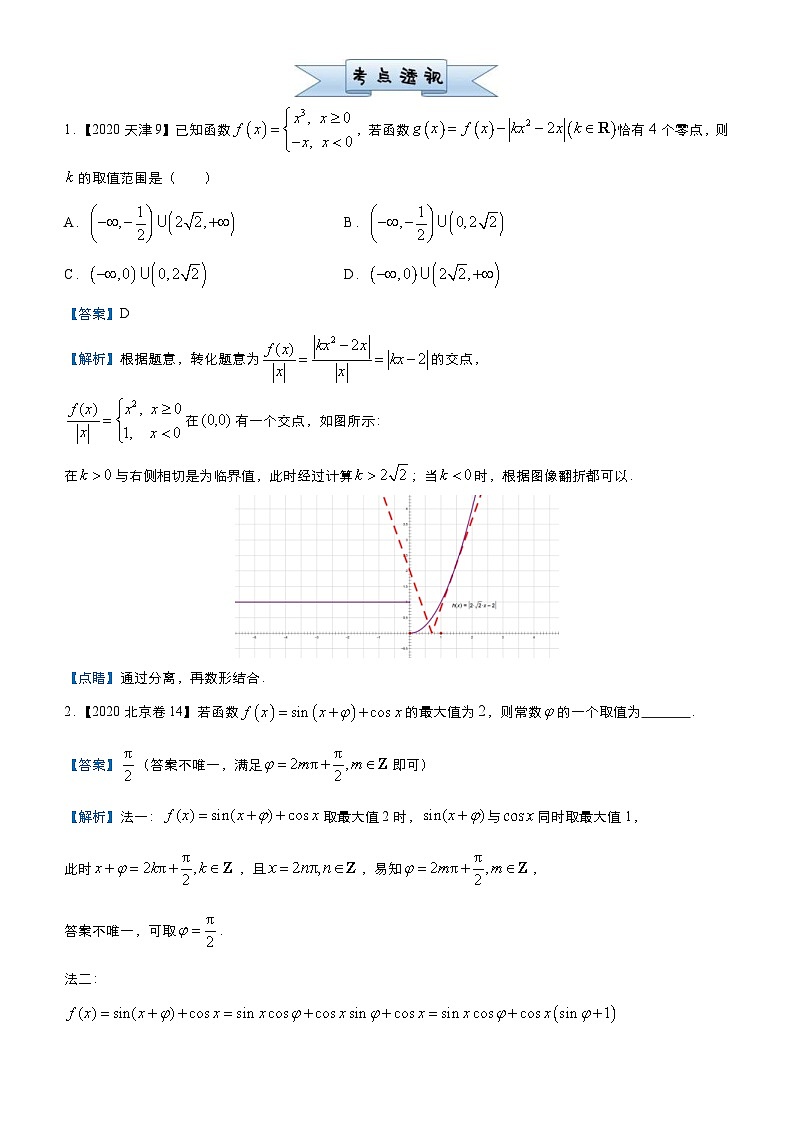
1．【2020天津9】已知函数 SKIPIF 1 < 0 ，若函数 SKIPIF 1 < 0 恰有4个零点，则 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【解析】根据题意，转化题意为 SKIPIF 1 < 0 的交点，
SKIPIF 1 < 0 在 SKIPIF 1 < 0 有一个交点，如图所示：
在 SKIPIF 1 < 0 与右侧相切是为临界值，此时经过计算 SKIPIF 1 < 0 ；当 SKIPIF 1 < 0 时，根据图像翻折都可以．
【点睛】通过分离，再数形结合．
2．【2020北京卷14】若函数 SKIPIF 1 < 0 的最大值为2，则常数 SKIPIF 1 < 0 的一个取值为 ．
【答案】 SKIPIF 1 < 0 （答案不唯一，满足 SKIPIF 1 < 0 即可）
【解析】法一： SKIPIF 1 < 0 取最大值2时， SKIPIF 1 < 0 与 SKIPIF 1 < 0 同时取最大值1，
此时 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，易知 SKIPIF 1 < 0 ，
答案不唯一，可取 SKIPIF 1 < 0 ．
法二：
SKIPIF 1 < 0 SKIPIF 1 < 0 ，
取最大值2时， SKIPIF 1 < 0 ，化简得 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
答案不唯一，可取 SKIPIF 1 < 0 ．
【点睛】由 SKIPIF 1 < 0 最大值为2，只可能 SKIPIF 1 < 0 与 SKIPIF 1 < 0 同时取1，
则可以求出 SKIPIF 1 < 0 满足的要求．
一、单选题．
1．函数 SKIPIF 1 < 0 的定义域是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【解析】∵函数 SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
∴函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，故选D．
2．设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【解析】由题意，∵ SKIPIF 1 < 0 ，
又由 SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，故选C．
3．当 SKIPIF 1 < 0 时，函数 SKIPIF 1 < 0 和 SKIPIF 1 < 0 的图象只能是（ ）
A．B．C．D．
【答案】B
【解析】由于 SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，∴可得：当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 为过点 SKIPIF 1 < 0 的增函数，
SKIPIF 1 < 0 ，函数 SKIPIF 1 < 0 为减函数，故选B．
4．已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的大小关系是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【解析】∵ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，故选B．
5．已知函数 SKIPIF 1 < 0 与 SKIPIF 1 < 0 互为反函数，函数 SKIPIF 1 < 0 的图象与 SKIPIF 1 < 0 的图象关于 SKIPIF 1 < 0 轴对称，
若 SKIPIF 1 < 0 ，则实数 SKIPIF 1 < 0 的值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【解析】∵函数 SKIPIF 1 < 0 与 SKIPIF 1 < 0 互为反函数，∴函数 SKIPIF 1 < 0 ，
∵函数 SKIPIF 1 < 0 的图象与 SKIPIF 1 < 0 的图象关于 SKIPIF 1 < 0 轴对称，∴函数 SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，故选D．
6．若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B．1C． SKIPIF 1 < 0 D．2
【答案】B
【解析】∵ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，故选B．
7．已知 SKIPIF 1 < 0 是定义在 SKIPIF 1 < 0 上的奇函数，且 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B．0C．3D．2018
【答案】C
【解析】∵ SKIPIF 1 < 0 为 SKIPIF 1 < 0 的奇函数，∴ SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，
又由 SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 是周期为4的函数，
又 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
故选C．
8．已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的大小关系为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【解析】∵ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；当 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴函数在 SKIPIF 1 < 0 上增函数，在 SKIPIF 1 < 0 上减函数，∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，故选C．
9．函数 SKIPIF 1 < 0 ，若函数 SKIPIF 1 < 0 只一个零点，则 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】A
【解析】∵ SKIPIF 1 < 0 只有一个零点，∴ SKIPIF 1 < 0 与 SKIPIF 1 < 0 只有一个交点，
作出函数 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的图像， SKIPIF 1 < 0 与 SKIPIF 1 < 0 只有一个交点，
则 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ， SKIPIF 1 < 0 与 SKIPIF 1 < 0 只有一个交点，它们则相切，
∵ SKIPIF 1 < 0 ，令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，故切点为 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
综上所述， SKIPIF 1 < 0 的取值范围为 SKIPIF 1 < 0 ，故选A．
二、多选题．
10．设函数 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A．是奇函数，且在 SKIPIF 1 < 0 单调递增B．是奇函数，且在 SKIPIF 1 < 0 单调递增
C．是偶函数，且在 SKIPIF 1 < 0 单调递增D．是偶函数，且在 SKIPIF 1 < 0 单调递减
【答案】AB
【解析】 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上为单调递增函数，则 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上为单调递减函数，
结论：增函数-减函数=增函数，所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上为单调递增函数．
11．已知函数 SKIPIF 1 < 0 ，则（ ）
A． SKIPIF 1 < 0 的最小值为2B． SKIPIF 1 < 0 的图像关于 SKIPIF 1 < 0 中心对称
C． SKIPIF 1 < 0 的图像关于直线 SKIPIF 1 < 0 对称D． SKIPIF 1 < 0 的图像关于直线 SKIPIF 1 < 0 对称
【答案】BD
【解析】由于 SKIPIF 1 < 0 ，A错误；
SKIPIF 1 < 0 为奇函数，B正确；
SKIPIF 1 < 0 不成立，C错误；
SKIPIF 1 < 0 在定义域上恒成立，则D正确．
三、填空题．
12．已知 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，函数 SKIPIF 1 < 0 的图象恒过点 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 在幂函数图像上，
则 SKIPIF 1 < 0 __________．
【答案】 SKIPIF 1 < 0
【解析】∵ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
∴点 SKIPIF 1 < 0 的坐标是 SKIPIF 1 < 0 ．
由题意令 SKIPIF 1 < 0 ，由于图象过点 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，故答案为 SKIPIF 1 < 0 ．
13．【2018北京卷理13】能说明“若 SKIPIF 1 < 0 对任意的 SKIPIF 1 < 0 都成立，则 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上是增函数”
为假命题的一个函数是 ．
【答案】 SKIPIF 1 < 0
【解析】函数的单调性，答案不唯一．
14．【2020全国3卷理16】关于函数 SKIPIF 1 < 0 有如下四个命题：
① SKIPIF 1 < 0 的图像关于y轴对称；
② SKIPIF 1 < 0 的图像关于原点对称；
③ SKIPIF 1 < 0 的图像关于直线 SKIPIF 1 < 0 对称；
④ SKIPIF 1 < 0 的最小值为2．
其中所有真命题的序号是_________．
【答案】②③
【解析】对于①，由 SKIPIF 1 < 0 知函数定义域为 SKIPIF 1 < 0 ，定义域关于原点对称，
SKIPIF 1 < 0 ，该函数为奇函数关于原点对称，
故①错，②为正确；
对于③，由 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称，
③正确；
对于④，令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
∴由 SKIPIF 1 < 0 可知 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 无最小值，错误，
综上所述，真命题的序号是②③．
增函数
减函数
定义
一般地，设函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，如果对于定义域 SKIPIF 1 < 0 内某个区间D上的任意两个自变量的值 SKIPIF 1 < 0
当 SKIPIF 1 < 0 时，都有 SKIPIF 1 < 0 ，那么就说函数 SKIPIF 1 < 0 在区间D上是增函数
当 SKIPIF 1 < 0 时，都有 SKIPIF 1 < 0 ，那么就说函数 SKIPIF 1 < 0 在区间D上是减函数
图象描述
自左向右看图象是上升的
自左向右看图象是下降的
前提
设函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，如果存在实数 SKIPIF 1 < 0 满足
条件
（1）对于任意的 SKIPIF 1 < 0 ，都有 SKIPIF 1 < 0 ；
（2）存在 SKIPIF 1 < 0 ，使得 SKIPIF 1 < 0
（3）对于任意的 SKIPIF 1 < 0 ，都有 SKIPIF 1 < 0 ；
（4）存在 SKIPIF 1 < 0 ，使得 SKIPIF 1 < 0
结论
SKIPIF 1 < 0 为最大值
SKIPIF 1 < 0 为最小值
奇偶性
定义
图象特点
偶函数
一般地，如果对于函数 SKIPIF 1 < 0 的定义域内任意一个 SKIPIF 1 < 0 ，都有 SKIPIF 1 < 0 ，那么函数 SKIPIF 1 < 0 就叫做偶函数
关于y对称
奇函数
一般地，如果对于函数 SKIPIF 1 < 0 的定义域内任意一个 SKIPIF 1 < 0 ，都有 SKIPIF 1 < 0 ，那么函数 SKIPIF 1 < 0 就叫做奇函数
关于原点对称