新高考数学三轮冲刺小题必练10 计数原理与概率（2份打包，原卷版+教师版）

这是一份新高考数学三轮冲刺小题必练10 计数原理与概率（2份打包，原卷版+教师版），文件包含新高考数学三轮冲刺小题必练10计数原理与概率原卷版doc、新高考数学三轮冲刺小题必练10计数原理与概率教师版doc等2份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。

1．掌握古典概率的基本特征，解决简单的概率实际问题，借助古典概型初步认识有限样本空间、随机事件，以及随机事件的概率．
2．能够根据实际问题的需求，选择恰当的抽样方法获取样本数据，重点提升数据分析、数学建模、逻辑推理和数学运算素养．
3．了解分类加法计数原理、分步乘法计数原理及其意义，利用计数原理推导排列数公式、组合数公式，能用多项式运算法则和计数原理证明二项式定理，会用二项式定理解决与二项展开式有关的简单问题．
1．【2020全国新高考Ⅰ卷】 SKIPIF 1 < 0 名同学到甲、乙、丙三个场馆做志愿者，每名同学只去 SKIPIF 1 < 0 个场馆，甲场馆安排 SKIPIF 1 < 0 名，乙场馆安排 SKIPIF 1 < 0 名，丙场馆安排 SKIPIF 1 < 0 名，则不同的安排方法共有（ ）
A． SKIPIF 1 < 0 种B． SKIPIF 1 < 0 种C． SKIPIF 1 < 0 种D． SKIPIF 1 < 0 种
2．【2020全国II卷理科】在新冠肺炎疫情防控期间，某超市开通网上销售业务，每天能完成 SKIPIF 1 < 0 份订单的配货，由于订单量大幅增加，导致订单积压为解决困难，许多志愿者踊跃报名参加配货工作，已知该超市某日积压 SKIPIF 1 < 0 份订单未配货，预计第二天的新订单超过 SKIPIF 1 < 0 份的概率为 SKIPIF 1 < 0 ．志愿者每人每天完成 SKIPIF 1 < 0 份订单的配货，为使第二天完成积压订单及当日订单的配货的概率不小于 SKIPIF 1 < 0 ，则至少需要志愿者（ ）
A． SKIPIF 1 < 0 名B． SKIPIF 1 < 0 名C． SKIPIF 1 < 0 名D． SKIPIF 1 < 0 名
一、单选题．
1．某电视台一个综艺栏目对六个不同的节目排演出顺序，最前只能排甲或乙，最后不能排甲，则不同的排法共有（ ）
A． SKIPIF 1 < 0 种B． SKIPIF 1 < 0 种C． SKIPIF 1 < 0 种D． SKIPIF 1 < 0 种
2．某班班会准备从甲、乙等 SKIPIF 1 < 0 名学生中选派 SKIPIF 1 < 0 名学生发言，要求甲、乙两人至少有一人参加．当甲乙同时参加时，他们两人的发言不能相邻．那么不同的发言顺序的和数为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
3．某校毕业典礼由 SKIPIF 1 < 0 个节目组成，考虑整体效果，对节目演出顺序有如下要求：节目甲必须排在前三位，
且节目丙、丁必须排在一起，则该校毕业典礼节目演出顺序的编排方案共有（ ）
A． SKIPIF 1 < 0 种B． SKIPIF 1 < 0 种C． SKIPIF 1 < 0 种D． SKIPIF 1 < 0 种
4．若二项式 SKIPIF 1 < 0 的展开式中 SKIPIF 1 < 0 的系数是 SKIPIF 1 < 0 ，则实数 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
5． SKIPIF 1 < 0 展开式中，各项系数之和为 SKIPIF 1 < 0 ，则展开式中的常数项为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
6．“暑假”期间，三个家庭（每家均为一对夫妇和一个孩子）去“沈阳世博园”游玩，在某一景区前合影留念，要求前排站三个小孩，后排为三对夫妇，则每对夫妇均相邻，且小孩恰与自家父母排列的顺序一致的概率是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
7．已知集合 SKIPIF 1 < 0 ，若从集合 SKIPIF 1 < 0 中任取 SKIPIF 1 < 0 个不同的数，则这三个数可以作为三角形三边长的概率为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
8．中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹，用于装点生活或配合其他民俗活动的民间艺术，蕴涵了极致的数学美和丰富的传统文化信息．现有一幅剪纸的设计图，其中的 SKIPIF 1 < 0 个小圆均过正方形的中心，且内切于正方形的两邻边．若在正方形内随机取一点，则该点取自黑色部分的概率为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
二、多选题．
9．为弘扬我国古代的“六艺文化”，某夏令营主办单位计划利用暑期开设“礼”“乐”“射”“御”“书”“数”六门体验课程，每周一门，连续开设六周．则（ ）
A．某学生从中选 SKIPIF 1 < 0 门，共有 SKIPIF 1 < 0 种选法
B．课程“射”“御”排在不相邻两周，共有 SKIPIF 1 < 0 种排法
C．课程“礼”“书”“数”排在相邻三周，共有 SKIPIF 1 < 0 种排法
D．课程“乐”不排在第一周，课程“御”不排在最后一周，共有 SKIPIF 1 < 0 种排法
10．已知二项式 SKIPIF 1 < 0 的展开式中第 SKIPIF 1 < 0 项与第 SKIPIF 1 < 0 项的二项式系数之比是 SKIPIF 1 < 0 ，则下列说法正确的是（ ）
A．所有项的系数之和为 SKIPIF 1 < 0 B．所有项的系数之和为 SKIPIF 1 < 0
C．含 SKIPIF 1 < 0 的项的系数为 SKIPIF 1 < 0 D．含 SKIPIF 1 < 0 的项的系数为 SKIPIF 1 < 0
11．一袋中有大小相同的 SKIPIF 1 < 0 个红球和 SKIPIF 1 < 0 个白球，给出下列结论：①从中任取 SKIPIF 1 < 0 球，恰有一个白球的概率是 SKIPIF 1 < 0 ；②从中有放回的取球 SKIPIF 1 < 0 次，每次任取一球，恰好有两次白球的概率为 SKIPIF 1 < 0 ；③现从中不放回的取球 SKIPIF 1 < 0 次，每次任取 SKIPIF 1 < 0 球，则在第一次取到红球后，第二次再次取到红球的概率为 SKIPIF 1 < 0 ；④从中有放回的取球 SKIPIF 1 < 0 次，每次任取一球，则至少有一次取到红球的概率为 SKIPIF 1 < 0 ．则其中正确命题的序号是（ ）
A．①B．②C．③D．④
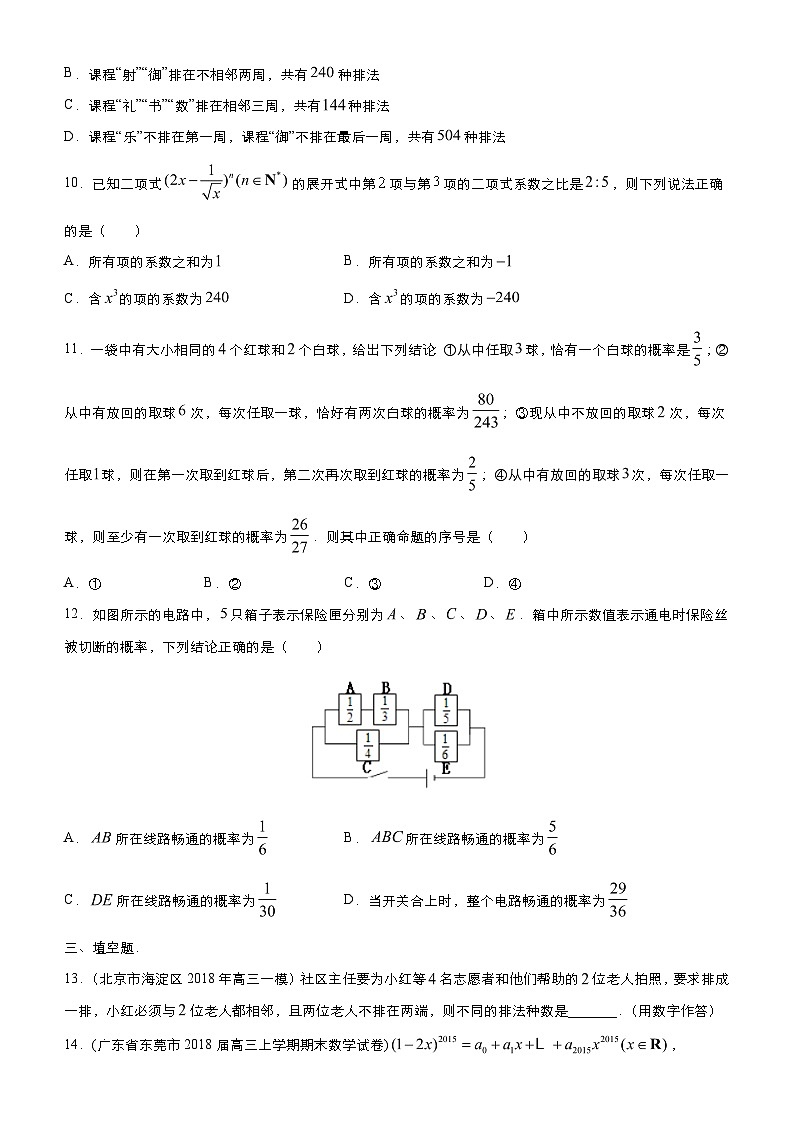
12．如图所示的电路中， SKIPIF 1 < 0 只箱子表示保险匣分别为 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ．箱中所示数值表示通电时保险丝被切断的概率，下列结论正确的是（ ）
A． SKIPIF 1 < 0 所在线路畅通的概率为 SKIPIF 1 < 0 B． SKIPIF 1 < 0 所在线路畅通的概率为 SKIPIF 1 < 0
C． SKIPIF 1 < 0 所在线路畅通的概率为 SKIPIF 1 < 0 D．当开关合上时，整个电路畅通的概率为 SKIPIF 1 < 0
三、填空题．
13．（北京市海淀区2018年高三一模）社区主任要为小红等 SKIPIF 1 < 0 名志愿者和他们帮助的 SKIPIF 1 < 0 位老人拍照，要求排成一排，小红必须与 SKIPIF 1 < 0 位老人都相邻，且两位老人不排在两端，则不同的排法种数是_______．（用数字作答）
14．(广东省东莞市2018届高三上学期期末数学试卷) SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 的值为________．
15．（山西省忻州一中、临汾一中2020届联考） SKIPIF 1 < 0 是半径为 SKIPIF 1 < 0 的圆周上一个定点，在圆周上等可能任取一点 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，则弦 SKIPIF 1 < 0 的长度超过 SKIPIF 1 < 0 的概率是_______．
16．已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 满足约束条件 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 的最小值为 SKIPIF 1 < 0 ．
（1）常数 SKIPIF 1 < 0 ________；
（2）向上述不等式组所表示的平面区域 SKIPIF 1 < 0 内随机投石子，则石子落在该区域内的最大圆内的概率为 SKIPIF 1 < 0 _____．
答案与解析
1．【答案】C
【解析】 SKIPIF 1 < 0 ．
【点睛】本题主要考查计数原理的相关知识，考查数学运算．
2．【答案】B
【解析】由题意知超市第二天能完成 SKIPIF 1 < 0 份订单的配货，
如果没有志愿者帮忙，则超市第二天共会积压超过 SKIPIF 1 < 0 份订单的概率为 SKIPIF 1 < 0 ，
因此要使第二天完成积压订单及当日订单的配货的概率不小于 SKIPIF 1 < 0 ，
至少需要志愿者 SKIPIF 1 < 0 （名），故选B．
【点睛】本题主要考查概率知识在生活中的应用，考查数学运算和数据分析．
一、单选题．
1．【答案】B
【解析】最前排甲，共有 SKIPIF 1 < 0 种，
最前只排乙，最后不能排甲，有 SKIPIF 1 < 0 种，
根据加法原理可得，共有 SKIPIF 1 < 0 种，故选B．
2．【答案】C
【解析】根据题意，分 SKIPIF 1 < 0 种情况讨论，若只有甲乙其中一人参加，有 SKIPIF 1 < 0 种情况；
若甲乙两人都参加，有 SKIPIF 1 < 0 种情况，其中甲乙相邻的有 SKIPIF 1 < 0 种情况，
则不同的发言顺序种数为 SKIPIF 1 < 0 种，故选C．
3．【答案】A
【解析】根据题意，由于节目甲必须排在前三位，分 SKIPIF 1 < 0 种情况讨论：
①甲排在第一位，节目丙、丁必须排在一起，则丁、丙相邻的位置有 SKIPIF 1 < 0 个，考虑两者的顺序，有 SKIPIF 1 < 0 种情况，
将剩下的 SKIPIF 1 < 0 个节目全排列，安排在其他三个位置，有 SKIPIF 1 < 0 种安排方法，
则此时有 SKIPIF 1 < 0 种编排方法；
②甲排在第二位，节目丙、丁必须排在一起，则丁、丙相邻的位置有 SKIPIF 1 < 0 个，考虑两者的顺序，有 SKIPIF 1 < 0 种情况，
将剩下的 SKIPIF 1 < 0 个节目全排列，安排在其他三个位置，有 SKIPIF 1 < 0 安排方法，
则此时有 SKIPIF 1 < 0 种编排方法；
③甲排在第三位，节目丙、丁必须排在一起，则丁、丙相邻的位置有 SKIPIF 1 < 0 个，考虑两者的顺序，有 SKIPIF 1 < 0 种情况，
将剩下的 SKIPIF 1 < 0 个节目全排列，安排在其他三个位置，有 SKIPIF 1 < 0 种安排方法，
则此时有 SKIPIF 1 < 0 种编排方法，
则符合题意要求的编排方法有 SKIPIF 1 < 0 种，故选A．
4．【答案】C
【解析】二项式 SKIPIF 1 < 0 的展开式，即 SKIPIF 1 < 0 的展开式中 SKIPIF 1 < 0 项的系数为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，令 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
代入得 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，故选C．
5．【答案】D
【解析】 SKIPIF 1 < 0 展开式中，各项系数之和为 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
∵展开式中 SKIPIF 1 < 0 的一项为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的 SKIPIF 1 < 0 此项为 SKIPIF 1 < 0 ，
展开式中的常数项为 SKIPIF 1 < 0 ，故选D．
6．【答案】B
【解析】前排站三个小孩，后排为三对夫妇的排列为 SKIPIF 1 < 0 种，
前排站三个小孩，后排为三对夫妇，则每对夫妇均相邻，且小孩恰与自家父母排列的顺序一致，
故有 SKIPIF 1 < 0 种，
故每对夫妇均相邻，且小孩恰与自家父母排列的顺序一致的概率 SKIPIF 1 < 0 ，故选B．
7．【答案】B
【解析】不妨设取出的三个数为 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ，能够成三角形，
则有以下几种情况；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 一共有 SKIPIF 1 < 0 组，
∴所求的概率为 SKIPIF 1 < 0 ．
8．【答案】A
【解析】分析题意可知，阴影部分刚好可以拼凑成一个圆形，
设圆的半径为 SKIPIF 1 < 0 ，该正方形的边长为 SKIPIF 1 < 0 ，则对于正方形的对角线而言，可以分为三个部分，第一个部分为正方形的对角线上的顶点到圆心的距离，两圆的圆心距，对角线上顶点到圆心的距离，
故 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
故概率 SKIPIF 1 < 0 ，故选A．
二、多选题．
9．【答案】CD
【解析】 SKIPIF 1 < 0 门中选 SKIPIF 1 < 0 门共有 SKIPIF 1 < 0 种，故A错误；
课程“射”“御”排在不相邻两周，共有 SKIPIF 1 < 0 种排法，故B错误；
课程“礼”“书”“数”排在相邻三周，共有 SKIPIF 1 < 0 种排法，故C正确；
课程“乐”不排在第一周，课程“御”不排在最后一周，共有 SKIPIF 1 < 0 种排法，故D正确．
10．【答案】AC
【解析】二项式 SKIPIF 1 < 0 展开式通项为： SKIPIF 1 < 0 ，
因为展开式中第 SKIPIF 1 < 0 项与第 SKIPIF 1 < 0 项的二项式系数之比是 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ；
则该二项式为 SKIPIF 1 < 0 ，令 SKIPIF 1 < 0 ，则所有项的系数之和为 SKIPIF 1 < 0 ，故A正确，B错误；
则展开式的通项公式为 SKIPIF 1 < 0 ，
令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，因此含 SKIPIF 1 < 0 的项的系数为 SKIPIF 1 < 0 ，故C正确，D错误．
11．【答案】ABD
【解析】一袋中有大小相同的 SKIPIF 1 < 0 个红球和 SKIPIF 1 < 0 个白球，
①从中任取 SKIPIF 1 < 0 球，恰有一个白球的概率是 SKIPIF 1 < 0 ，故正确；
②从中有放回的取球 SKIPIF 1 < 0 次，每次任取一球，每次抽到白球的概率为 SKIPIF 1 < 0 ，
则恰好有两次白球的概率为 SKIPIF 1 < 0 ，故正确；
③现从中不放回的取球 SKIPIF 1 < 0 次，每次任取 SKIPIF 1 < 0 球，则在第一次取到红球后，第二次再次取到红球的概率为 SKIPIF 1 < 0 ，故错误；
④从中有放回的取球3次，每次任取一球，每次抽到红球的概率为 SKIPIF 1 < 0 ，
则至少有一次取到红球的概率为 SKIPIF 1 < 0 ，故正确．
12．【答案】BD
【解析】由题意知， SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 保险闸被切断的概率分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 、 SKIPIF 1 < 0 两个盒子畅通的概率为 SKIPIF 1 < 0 ，因此A错误；
SKIPIF 1 < 0 、 SKIPIF 1 < 0 两个盒子并联后畅通的概率为 SKIPIF 1 < 0 ，因此C错误；
SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 三个盘子混联后畅通的概率为 SKIPIF 1 < 0 ，B正确；
根据上述分析可知，当开关合上时，电路畅通的概率为 SKIPIF 1 < 0 ，D正确．
三、填空题．
13．【答案】24
【解析】首先小红必须与 SKIPIF 1 < 0 位老人都相邻有 SKIPIF 1 < 0 种排法，将三人看成一个整体，从剩下的 SKIPIF 1 < 0 名志愿者中选出两人排在两端有 SKIPIF 1 < 0 种，剩下的一名志愿者与小红等三人可乱排有 SKIPIF 1 < 0 种，
根据分步计数原理可得不同的排法种数 SKIPIF 1 < 0 种．
14．【答案】 SKIPIF 1 < 0
【解析】由题意得 SKIPIF 1 < 0 ，取 SKIPIF 1 < 0 ，代入二式项得 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
15．【答案】 SKIPIF 1 < 0
【解析】根据题意可得，满足条件：“弦 SKIPIF 1 < 0 的长度超过”对应的弧，其构成的区域是圆的 SKIPIF 1 < 0 ，
故弦 SKIPIF 1 < 0 的长度超过 SKIPIF 1 < 0 的概率 SKIPIF 1 < 0 ．
16．【答案】（1） SKIPIF 1 < 0 ；（2） SKIPIF 1 < 0
【解析】由 SKIPIF 1 < 0 的几何意义可知，
当 SKIPIF 1 < 0 经过 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的交点 SKIPIF 1 < 0 时，取得最小值 SKIPIF 1 < 0 ，
故 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ．
（2）由（1）可知，在直角坐标系内画出可行域如图，易求得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
而 SKIPIF 1 < 0 为等腰直角三角形，且斜边 SKIPIF 1 < 0 ，其内切圆半径 SKIPIF 1 < 0 ，
所以平面区域 SKIPIF 1 < 0 内圆的最大面积是 SKIPIF 1 < 0 ，
又平面区域 SKIPIF 1 < 0 的面积 SKIPIF 1 < 0 ，
所以所求概率 SKIPIF 1 < 0 ．