第四章　§4.8　正弦定理、余弦定理-2025年新高考数学一轮复习（课件+讲义+练习）

这是一份第四章　§4.8　正弦定理、余弦定理-2025年新高考数学一轮复习（课件+讲义+练习），文件包含第四章§48正弦定理余弦定理pptx、第四章§48正弦定理余弦定理教师版docx、第四章§48正弦定理余弦定理同步练习docx、第四章§48正弦定理余弦定理-2025新高考一轮复习讲义学生版docx等4份课件配套教学资源，其中PPT共60页， 欢迎下载使用。

1、揣摩例题。课本上和老师讲解的例题，一般都具有一定的典型性和代表性。要认真研究，深刻理解，要透过“样板”，学会通过逻辑思维，灵活运用所学知识去分析问题和解决问题，特别是要学习分析问题的思路、解决问题的方法，并能总结出解题的规律。 2、精练习题。复习时不要搞“题海战术”，应在老师的指导下，选一些源于课本的变式题，或体现基本概念、基本方法的基本题，通过解题来提高思维能力和解题技巧，加深对所学知识的深入理解。在解题时，要独立思考，一题多思，一题多解，反复玩味，悟出道理。 3、加强审题的规范性。每每大考过后，总有同学抱怨没考好，纠其原因是考试时没有注意审题。审题决定了成功与否，不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系，确定解题思路 。 4、重视错题。“错误是最好的老师”，但更重要的是寻找错因，及时进行总结，三五个字，一两句话都行，言简意赅，切中要害，以利于吸取教训，力求相同的错误不犯第二次。
§4.8　正弦定理、余弦定理
1.掌握正弦定理、余弦定理及其变形.2.理解三角形的面积公式并能应用.3.能利用正弦定理、余弦定理解决一些简单的三角形度量问题.
第一部分 落实主干知识
第二部分 探究核心题型
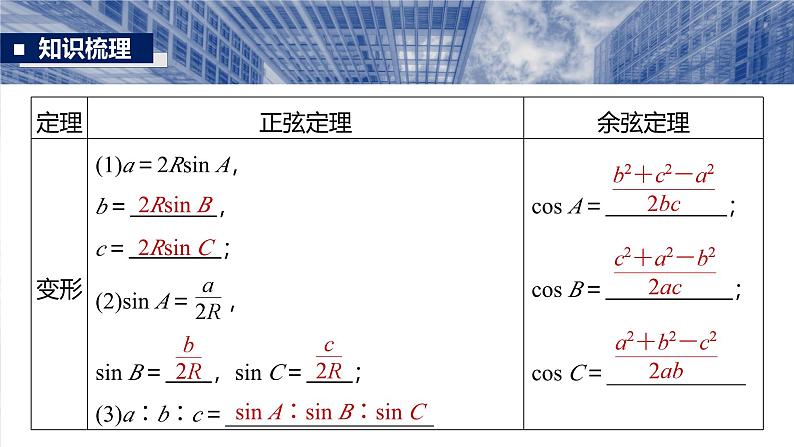
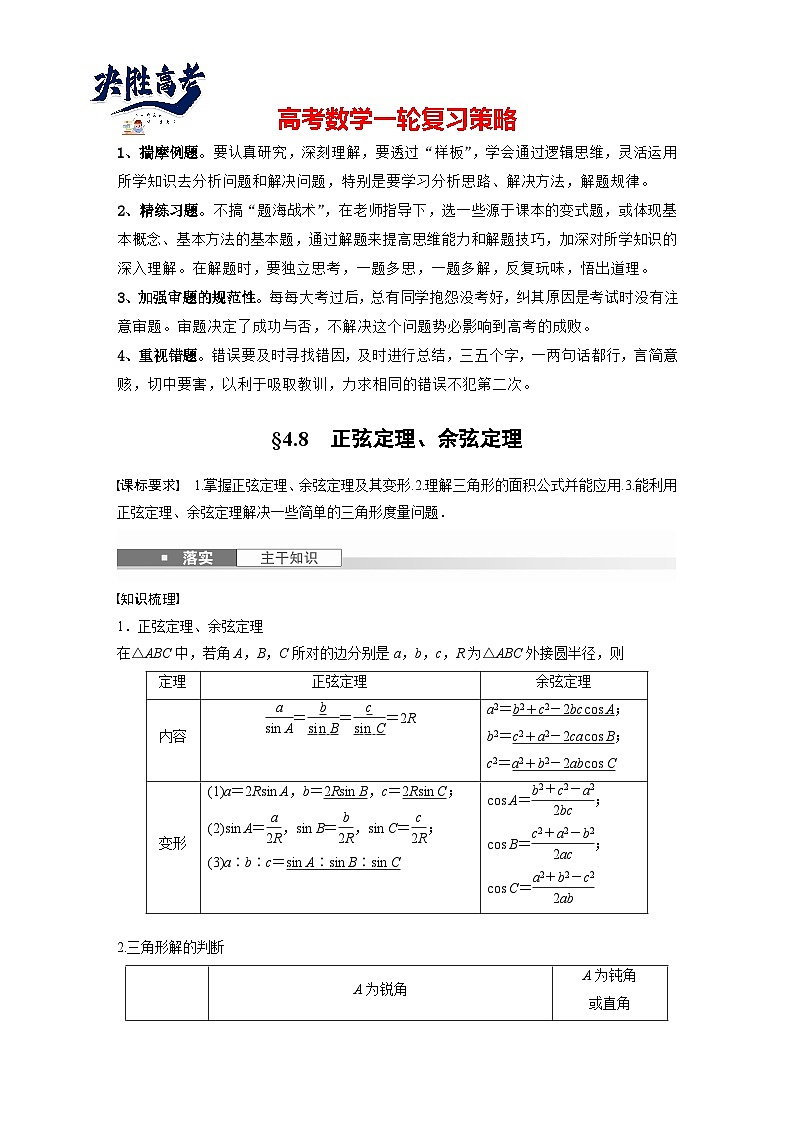
1.正弦定理、余弦定理在△ABC中，若角A，B，C所对的边分别是a，b，c，R为△ABC外接圆半径，则
b2＋c2－2bccs A
c2＋a2－2cacs B
a2＋b2－2abcs C
sin A∶sin B∶sin C
(2)S＝ ＝ ＝ ；
(3)S＝ (r为三角形的内切圆半径).
在△ABC中，常有以下结论：(1)∠A＋∠B＋∠C＝π.(2)任意两边之和大于第三边，任意两边之差小于第三边.(3)a>b⇔A>B⇔sin A>sin B，cs A(5)三角形中的射影定理在△ABC中，a＝bcs C＋ccs B；b＝acs C＋ccs A；c＝bcs A＋acs B.
1.判断下列结论是否正确.(请在括号中打“√”或“×”)(1)三角形中三边之比等于相应的三个内角的余弦值之比.(　　)(2)在△ABC中，若sin A>sin B，则a>b.(　　)(3)在△ABC的六个元素中，已知任意三个元素可求其他元素.(　　)(4)当b2＋c2－a2>0时，△ABC为锐角三角形.(　　)
2.(必修第二册P44T2改编)在△ABC中，AB＝5，AC＝3，BC＝7，则∠BAC等于
在△ABC中，设AB＝c＝5，AC＝b＝3，BC＝a＝7，由余弦定理得
因为∠BAC为△ABC的内角，
3.在△ABC中，a，b，c分别为角A，B，C所对的边，已知b＝40，c＝20，C＝60°，则此三角形的解的情况是A.有一解B.有两解C.无解D.有解但解的个数不确定
∴角B不存在，即此三角形无解.
4.记△ABC的内角A，B，C的对边分别为a，b，c，面积为 ，B＝60°，a2＋c2＝3ac，则b＝ .
则ac＝4，所以a2＋c2＝3ac＝3×4＝12，
题型一　利用正弦、余弦定理解三角形
例1　(1)(2023·榆林模拟)△ABC的内角A，B，C所对的边分别为a，b，c，若asin A＋(b＋λa)sin B＝csin C，则λ的取值范围为A.(－2,2) B.(0,2)C.[－2,2] D.[0,2]
因为asin A＋(b＋λa)sin B＝csin C，由正弦定理得c2＝a2＋b2＋λab，由余弦定理知c2＝a2＋b2－2abcs C，所以λ＝－2cs C，因为C∈(0，π)，所以cs C∈(－1,1)，故λ∈(－2,2).
(2)(2024·兰州模拟)用长度为1,4,8,9的4根细木棒围成一个三角形(允许连接，不允许折断)，则其中某个三角形外接圆的直径可以是_________________(写出一个答案即可).
4根细木棒围成的三角形的三边长可以为5,8,9，设边长为9的边所对的角为θ，该三角形外接圆的半径为R，
解三角形时，如果式子中含有角的余弦或边的二次式，要考虑用余弦定理；如果式子中含有角的正弦或边的一次式，则考虑用正弦定理，以上特征都不明显时，则要考虑两个定理都有可能用到.
又因为0°a，A＝45°，所以C＝60°或120°.
由正弦定理及bsin 2A＝asin B，得2sin Bsin Acs A＝sin Asin B，
题型二　正弦定理、余弦定理的简单应用
命题点1　三角形的形状判断
注：如果选择多个条件分别解答，则按第一个解答计分.
∴a2－b2＋ac－bc＝0，∴(a－b)(a＋b＋c)＝0，∴a＝b.若选①，则△ABC为等边三角形.推理如下：由a(sin A－sin B)＝(c－b)(sin C＋sin B)及正弦定理，得a(a－b)＝(c－b)(c＋b)，
即a2＋b2－c2＝ab.
∴△ABC为等边三角形.若选②，则△ABC为等腰直角三角形.推理如下：
∴△ABC为等腰直角三角形.
判断三角形形状的两种思路(1)化边：通过因式分解、配方等得出边的相应关系，从而判断三角形的形状.(2)化角：通过三角恒等变换，得出内角的关系，从而判断三角形的形状.此时要注意应用A＋B＋C＝π这个结论.
命题点2　三角形的面积例3　(10分)(2023·新高考全国Ⅰ)已知在△ABC中，A＋B＝3C，2sin(A－C)＝sin B.(1)求sin A；[切入点：由A，B，C关系求角C及代换sin B](2)设AB＝5，求AB边上的高.[关键点：由A，B，C关系求sin B][思路分析](1)由A，B，C关系求角C→B＝π－(A＋C)代入化简→tan A→sin A(2)由角C，sin A→sin B→AC→等面积法求高
答题模板　规范答题不丢分
①处由A，B，C关系求角C
又2sin(A－C)＝
②处由B与A，C关系代换sin B
∴2sin Acs C－2cs Asin C＝sin Acs C＋cs Asin C，∴sin Acs C＝3cs Asin C，∴sin A＝3cs A，
即tan A＝3，(4分)
⑤处由B与A，C关系求sin B
三角形面积公式的应用原则
(2)与面积有关的问题，一般要用到正弦定理或余弦定理进行边和角的转化.
命题点3　与平面几何有关的问题例4　(2023·梅州模拟)△ABC的内角A，B，C的对边分别为a，b，c，已知2a＋b＝2ccs B.(1)求角C；
由2a＋b＝2ccs B，根据正弦定理可得2sin A＋sin B＝2sin Ccs B，则2sin(B＋C)＋sin B＝2sin Ccs B，所以2sin Bcs C＋2cs Bsin C＋sin B＝2sin Ccs B，整理得(2cs C＋1)sin B＝0，因为B，C均为三角形内角，所以B，C∈(0，π)，sin B≠0，
所以b＝2a，又由余弦定理可得c2＝a2＋b2－2abcs C，
解得a＝3，所以b＝6，又S△ABC＝S△ACD＋S△BCD，
在平面几何图形中研究或求与角有关的长度、角度、面积的最值、优化设计等问题时，通常是转化到三角形中，利用正、余弦定理通过运算的方法加以解决.在解决某些具体问题时，常先引入变量，如边长、角度等，然后把要解三角形的边或角用所设变量表示出来，再利用正、余弦定理列出方程，再解方程即可.若研究最值，常使用函数思想.
∴由a2＝b2＋c2－2bccs A，
(2)(2023·聊城模拟)已知△ABC的内角A，B，C所对的边分别为a，b，c，若a－b＝ccs B－ccs A，则△ABC的形状一定是A.等腰三角形 B.直角三角形C.等腰直角三角形 D.等腰或直角三角形
因为a－b＝ccs B－ccs A，所以由正弦定理得sin A－sin B＝sin Ccs B－sin Ccs A，因为sin A＝sin(B＋C)＝sin Bcs C＋cs Bsin C，sin B＝sin(A＋C)＝sin Acs C＋cs Asin C，所以sin Bcs C＋cs Bsin C－sin Acs C－cs Asin C＝sin Ccs B－sin Ccs A，
整理得sin Bcs C－sin Acs C＝0，所以(sin B－sin A)cs C＝0，所以sin B＝sin A或cs C＝0，
即△ABC的形状一定是等腰或直角三角形.
(3)(2023·宝鸡统考)在△ABC中，AB＝5，AC＝7，D为BC的中点，AD＝5，则BC等于
方法一　设BC＝2x，则BD＝CD＝x.
在△ABD中，由余弦定理的推论可得，
又∠ADC＋∠ADB＝π，
所以cs∠ADC＝－cs∠ADB，
所以BC2＝AB2＋AC2－2AB·AC·cs∠BAC
一、单项选择题1.在△ABC中，C＝60°，a＋2b＝8，sin A＝6sin B，则c等于
因为sin A＝6sin B，则由正弦定理得a＝6b，又a＋2b＝8，所以a＝6，b＝1，因为C＝60°，所以由余弦定理c2＝a2＋b2－2abcs C，
2.在△ABC中，内角A，B，C的对边a，b，c依次成等差数列，且B＝ ，则△ABC的形状为A.等边三角形B.直角边不相等的直角三角形C.等腰直角三角形D.钝角三角形
所以由正弦定理得ac＝b2－a2－c2，即a2＋c2－b2＝－ac，
A.1 B.2C.3 D.4
∴在△ABD中，由余弦定理得
即a2＋4c2－2ac＝4，
解得ac＝2，①∴a2＋4c2－2ac＝4＝2ac，
即4c2－4ac＋a2＝0，∴(2c－a)2＝0，即a＝2c，②将②代入①得2c2＝2，解得c＝1或c＝－1(舍去).
设BC＝CD＝x>0，在△ABC中，由余弦定理，得AC2＝36＋x2－2×6xcs B＝28，即x2＋8＝12xcs B，①又在△ACD中，由余弦定理，得AC2＝4＋x2－2×2xcs D＝28，即x2－24＝4xcs D，②因为B＋D＝π，
则cs D＝cs(π－B)＝－cs B，
设△ABC中，角A，B，C的对边为a，b，c，∵cs2A＋sin2B＋sin2C＋sin Bsin C＝1，即sin2B＋sin2C＋sin Bsin C＝sin2A，∴b2＋c2＋bc＝a2，
即b＝3，∴a2＝b2＋c2＋bc＝32＋22＋3×2＝19，
根据余弦定理可知a2＋c2－b2＝2accs B，
8.已知△ABC的内角A，B，C所对的边分别为a，b，c，下列四个命题中正确的是A.若acs A＝bcs B，则△ABC是等腰三角形B.若bcs C＋ccs B＝b，则△ABC是等腰三角形
对于A，若acs A＝bcs B，则由正弦定理得sin Acs A＝sin Bcs B，∴sin 2A＝sin 2B，则2A＝2B或2A＋2B＝180°，即A＝B或A＋B＝90°，则△ABC为等腰三角形或直角三角形，故A错误；对于B，若bcs C＋ccs B＝b，则由正弦定理得sin Bcs C＋sin Ccs B＝sin(B＋C)＝sin A＝sin B，即A＝B，则△ABC是等腰三角形，故B正确；
对于D，由于B＝60°，b2＝ac，由余弦定理可得b2＝ac＝a2＋c2－ac，可得(a－c)2＝0，解得a＝c，故△ABC是等边三角形，故D错误.
所以2a·cs A＝c·cs B＋b·cs C，由正弦定理得2sin Acs A＝sin Ccs B＋sin Bcs C，即2sin Acs A＝sin(B＋C)＝sin A，因为sin A>0，
10.我国南宋著名数学家秦九韶在他的著作《数书九章》卷五的“田域类”中写道：问有沙田一段，有三斜，其小斜一十三里，中斜一十四里，大斜一十五里.里法三百步.欲知为田几何.意思是已知三角形沙田的三边长分别为13里、14里、15里，求三角形沙田的面积.则该沙田的面积为 平方里.
由题意画出△ABC(图略)，且AB＝13里，BC＝14里，AC＝15里，
由于0在△ADC中，AD⊥AC，AD＝1，
因为B＝180°－∠BAC－C＝60°－C，在△ABC中，
因为C∈(0，π)，所以sin C≠0，
在△ABC中，由余弦定理，
即7＝4＋c2＋2c，解得c＝1或c＝－3(舍去)，
由余弦定理得c2＝BD2＋AD2－2BD·ADcs∠ADB，
在△ACD中，由余弦定理得b2＝CD2＋AD2－2CD·ADcs∠ADC，
(2)若b2＋c2＝8，求b，c.
方法一　在△ABD与△ACD中，由余弦定理得
解得sin∠ADC＝1，而0<∠ADC<π，
方法二　在△ABC中，因为D为BC的中点，
15.(2023·渝中模拟)如图，设在△ABC中，AB＝BC＝AC，从顶点A连接对边BC上两点D，E，使得∠DAE＝30°，若BD＝16，CE＝5，则边长AB等于A.38 D.44
方法一　设AB＝x，∠BAD＝α，
在△EAC中，由正弦定理得
可以化简得x2－42x＋80＝0，解得x＝40，x＝2(舍去).方法二　设AB＝x，利用余弦定理得AD2＝x2＋162－16x，AE2＝x2＋52－5x，
则在△ADE中，由余弦定理得(x－21)2＝AD2＋AE2－2AD·AEcs 30°，x2－42x＋212＝x2＋162－16x＋x2＋52－5x－3x(x－21)，化简整理得x2－42x＋80＝0，即x＝40，x＝2(舍去).
A.等腰三角形B.直角三角形C.等腰直角三角形D.以上说法都不对
所以1＋cs A＝sin B＋sin C，③1＋cs B＝sin A＋sin C，④由③和④得1＋cs A－sin B＝1＋cs B－sin A，即sin A＋cs A＝sin B＋cs B，
因为A，B为三角形内角，
(1)若A＝B，由C＝π－A－B＝π－2A，将其代入③，得1＋cs A＝sin A＋sin 2A.变形得(sin A－cs A)2－(sin A－cs A)＝0，