第四章　§4.10　解三角形应用举例-2025年新高考数学一轮复习（课件+讲义+练习）

这是一份第四章　§4.10　解三角形应用举例-2025年新高考数学一轮复习（课件+讲义+练习），文件包含第四章§410解三角形应用举例pptx、第四章§410解三角形应用举例教师版docx、第四章§410解三角形应用举例同步练习docx、第四章§410解三角形应用举例-2025新高考一轮复习讲义学生版docx等4份课件配套教学资源，其中PPT共60页， 欢迎下载使用。

1、揣摩例题。课本上和老师讲解的例题，一般都具有一定的典型性和代表性。要认真研究，深刻理解，要透过“样板”，学会通过逻辑思维，灵活运用所学知识去分析问题和解决问题，特别是要学习分析问题的思路、解决问题的方法，并能总结出解题的规律。 2、精练习题。复习时不要搞“题海战术”，应在老师的指导下，选一些源于课本的变式题，或体现基本概念、基本方法的基本题，通过解题来提高思维能力和解题技巧，加深对所学知识的深入理解。在解题时，要独立思考，一题多思，一题多解，反复玩味，悟出道理。 3、加强审题的规范性。每每大考过后，总有同学抱怨没考好，纠其原因是考试时没有注意审题。审题决定了成功与否，不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系，确定解题思路 。 4、重视错题。“错误是最好的老师”，但更重要的是寻找错因，及时进行总结，三五个字，一两句话都行，言简意赅，切中要害，以利于吸取教训，力求相同的错误不犯第二次。
§4.10　解三角形应用举例
能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.
第一部分 落实主干知识
第二部分 探究核心题型
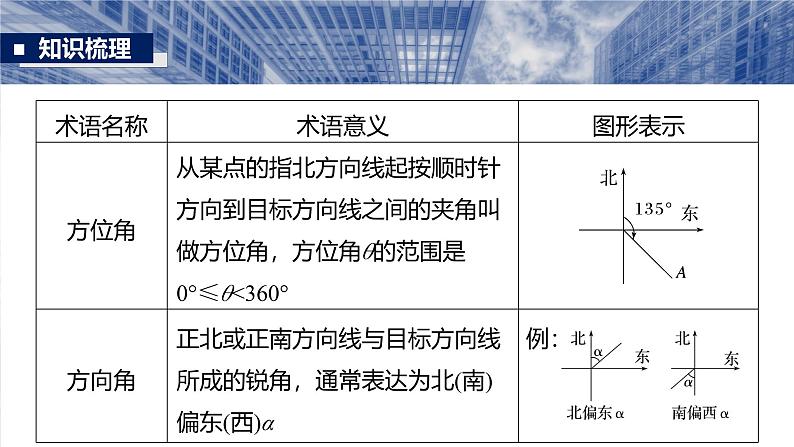
1.判断下列结论是否正确.(请在括号中打“√”或“×”)(1)西南方向与南偏西45°方向相同.(　　)(2)仰角和俯角都是铅垂线与目标视线所成的角，其范围为 .(　　)(3)方位角是从正北方向起按顺时针转到目标方向线之间的水平夹角.(　　)(4)若从A处望B处的仰角为α，从B处望A处的俯角为β，则α，β的关系为α＋β＝180°.(　　)
2.(必修第二册P51T3改编)如图，两座灯塔A和B与海岸观察站C的距离相等，灯塔A在观察站南偏西40°方向，灯塔B在观察站南偏东60°方向，则灯塔A在灯塔BA.北偏东10°方向 B.北偏西10°方向C.南偏东80°方向 D.南偏西80°方向
由题可知，∠CAB＝∠CBA＝40°，又∠BCD＝60°，所以∠CBD＝30°，所以∠DBA＝10°，因此灯塔A在灯塔B南偏西80°方向.
3.(必修第二册P50例10改编)如图所示，为测量某树的高度，在地面上选取A，B两点，从A，B两点分别测得树尖P的仰角为30°，45°，且A，B两点之间的距离为60 m，则树的高度为
在△ABP中，∠APB＝45°－30°＝15°，
由题意可知∠ACB＝60°，
例1　(1)如图，某市地面有四个5G基站A，B，C，D.已知基站C，D建在江的南岸，距离为10 km；基站A，B建在江的北岸，测得∠ACB＝45°，∠ACD＝30°，∠ADC＝120°，∠ADB＝75°，则基站A，B之间的距离为
在△ACD中，∠ACD＝30°，∠ADC＝120°，又∠ADB＝75°，
在△BCD中，∠CBD＝180°－(30°＋45°＋45°)＝60°，
在△ABD中，由余弦定理得AB2＝AD2＋BD2－2AD·BD·cs∠ADB
(2)(2024·厦门模拟)一艘海轮从A处出发，以每小时40海里的速度沿东偏南50°方向直线航行，30分钟后到达B处.在C处有一座灯塔，海轮在A处观察灯塔，其方向是东偏南20°，在B处观察灯塔，其方向是北偏东65°，那么B，C两点间的距离是
依题意，如图，在△ABC中，
距离问题的解题思路：这类实际应用题，实质就是解三角形问题，一般都离不开正弦定理和余弦定理，在解题中，首先要正确地画出符合题意的示意图，然后将问题转化为三角形问题去求解.注意：①基线的选取要恰当准确；②选取的三角形及正、余弦定理要恰当.
跟踪训练1　(1)(2023·绥化模拟)安邦河，在黑龙江省内有两条.一条属于松花江二级支流，位于黑龙江省中部，发源于小兴安岭支脉平顶山西坡；另一条属于松花江右岸支流，位于黑龙江省东部，发源于完达山支脉分水岗，自南向北流经双鸭山、集贤、桦川3个市县，在桦川县新城乡境内注入松花江.安邦河从双鸭山一中旁流过，其中一河段的两岸基本上是平行的，根据城建工程计划，需要测量出该河段的宽度，现在一侧岸边选取两点A，B并测得AB＝a，选取对岸一目标点C并测得∠ABC＝α，∠BAC＝β，则该段河流的宽度为
在△ABC中，由正弦定理得
(2)如图，为计算湖泊岸边两景点B与C之间的距离，在岸上选取A和D两点，现测得AB＝5 km，AD＝7 km，∠ABD＝60°，∠CBD＝23°，∠BCD＝117°，据以上条件可求得两景点B与C之间的距离为______ km(精确到0.1 km，参考数据：sin 40°≈0.643，sin 117°≈0.891).
在△ABD中，有AB＝5，AD＝7，∠ABD＝60°，由余弦定理可得，AD2＝AB2＋BD2－2AB·BDcs∠ABD，
整理可得BD2－5BD－24＝0，解得BD＝8或BD＝－3(舍去).在△BCD中，有BD＝8，∠CBD＝23°，∠BCD＝117°，所以∠BDC＝180°－∠BCD－∠CBD＝40°.
例2　(1)(2023·济宁统考)首钢滑雪大跳台(如图1)是冬奥历史上第一座与工业遗产再利用直接结合的竞赛场馆，大跳台的设计中融入了世界文化遗产敦煌壁画中“飞天”的元素.某校研究性学习小组为了估算赛道造型最高点A(如图2)距离地面的高度AB(AB与地面垂直)，在赛道一侧找到一座建筑物PQ，测得PQ的高度为25.4米，并从P点测得A点的仰角为30°；在赛道与建筑物PQ之间的地面上的点M处测得A点，P点的仰角分别为75°和30°(其中B，M，Q三点共线)，该学习小组利用这些数据估算得赛道造型最高点A距离地面的高度约为A.58 米 B.60 米C.66 米 D.68 米
由题意得∠AMB＝75°，∠PMQ＝30°，∠AMP＝75°，∠APM＝60°，∠PAM＝45°，
在△PAM中，由正弦定理得
在△ABM中，AB＝AM·sin∠AMB
(2)矗立在上饶市市民公园(如图1)的四门通天铜雕有着“四方迎客、通达天下”的美好寓意，也象征着上饶四省通衢，连南接北，通江达海，包容八方.如图2，某中学研究性学习小组为测量其高度，在和它底部O位于同一水平高度的共线三点A，B，C处测得铜雕顶端P处的仰角分别为 ，且AB＝BC＝20 m，则四门通天的高度为
在△BCO中，由余弦定理得
因为∠ABO＋∠OBC＝π，
高度问题的易错点(1)图形中为空间关系，极易当作平面问题处理，从而致错；(2)对仰角、俯角等概念理解不够深入，从而把握不准已知条件而致错.
跟踪训练2　(1)如图，在山脚A处测得山顶P的仰角为37°，沿坡角为23°的斜坡向上走28 m到达B处，在B处测得山顶P的仰角为53°，且A，B，P，C，Q在同一平面，则山的高度约为(参考数据：sin 37°≈0.6)A.30 m B.32 mC.34 m D.36 m
∠BAQ＝23°，∠BPA＝∠QPA－∠BPC＝53°－37°＝16°，∠PAB＝∠PAQ－∠BAQ＝37°－23°＝14°，∠PBA＝180°－16°－14°＝150°.
所以山的高度约为PQ＝AP·sin 37°＝50×0.6＝30(m).
(2)“伦敦眼”坐落在英国伦敦泰晤士河畔，是世界上首座观景摩天轮，又称“千禧之轮”，该摩天轮的半径为6(单位：10 m)，游客在乘坐舱P升到上半空鸟瞰伦敦建筑BC，伦敦眼与建筑之间的距离AB为12(单位：10 m)，游客在乘坐舱P看建筑BC的视角为θ.当乘坐舱P在伦敦眼的最高点D时，视角θ＝30°，则建筑BC的高度为__________.(单位：10 m)
当乘坐舱P在伦敦眼的最高点D时，如图所示，因为摩天轮的半径为6，所以AD＝12，又AB＝12，
因为∠DBA＝45°，所以∠DBC＝45°，因为∠CDB＝θ＝30°，所以∠DCB＝180°－45°－30°＝105°，
例3　已知在岛A南偏西38°方向，距岛A 3海里的B处有一艘救援艇.岛A处的一艘故障船正以10海里/小时的速度向岛A北偏西22°方向行驶，问救援艇朝何方向以多大速度行驶，恰好用0.5小时追赶上该故障船？
如图，设救援艇在C处追赶上故障船，D为岛A正南方向上一点，救援艇的速度为x海里/小时，结合题意知BC＝0.5x，AC＝5，∠BAC＝180°－38°－22°＝120°.
所以BC＝0.5x＝7，解得x＝14.
所以∠ABC＝38°，又∠BAD＝38°，所以BC∥AD，故救援艇以14海里/小时的速度向正北方向行驶，恰好用0.5小时追赶上该故障船.
角度问题的解题方法首先应明确方向角的含义，在解应用题时，分析题意，分清已知与所求，再根据题意正确画出示意图，这是最关键、最重要的一步，通过这一步可将实际问题转化成可用数学方法解决的问题，解题中也要注意体会正、余弦定理“联袂”使用的优点.
跟踪训练3　(1)(2023·南京模拟)如图所示，在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°，向山顶前进100 m到达B处，又测得C对于山坡的斜度为45°，若CD＝50 m，山坡对于地平面的坡度为θ，则cs θ等于
在△ABC中，∠ACB＝180°－∠BAC－∠ABC＝180°－15°－135°＝30°，
(2)甲船在A处观察乙船，乙船在它北偏东60°方向，相距a海里的B处，乙船向正北方向行驶，若甲船速度是乙船速度的 倍，甲船为了尽快追上乙船，朝北偏东θ方向前进，则θ＝________.
如图，设两船在C处相遇，
又因为0°<∠BAC<60°，所以∠BAC＝30°，所以θ＝60°－30°＝30°.
一、单项选择题1.如图，设A，B两点在河的两岸，在点A所在河岸边选一定点C，测量AC的距离为50 m，∠ACB＝30°，∠CAB＝105°，则A，B两点间的距离是
在△ABC中，∠ACB＝30°，∠CAB＝105°，所以∠ABC＝180°－30°－105°＝45°，
2.(2024·咸阳模拟)世界上最大的球形建筑物是位于瑞典斯德哥尔摩的爱立信球形体育馆(瑞典语：Ericssn Glbe)，在世界最大的瑞典太阳系模型中，由该体育场代表太阳的位置，其外形像一个大高尔夫球，可容纳16 000名观众观看表演和演唱会，或14 119名观众观看冰上曲棍球.如图，某数学兴趣小组为了测得爱立信球形体育馆的直径，在体育馆外围测得AB＝120 m，BC＝120 m，CD＝80 m，∠ABC＝60°，∠BCD＝120°(其中A，B，C，D四点共面)，据此可估计该体育馆的直径AD大约为(结果精确到1 m，参考数据： ≈2.646)A.98 m B.106 mC.117 m D.122 m
如图，连接AC，AD，在△ABC中，AB＝120 m，BC＝120 m，∠ABC＝60°，所以△ABC为等边三角形，所以AC＝120 m，∠ACD＝∠BCD－∠ACB＝60°，在△ACD中，由余弦定理可得AD2＝AC2＋CD2－2AC·CD·cs∠ACD，
3.如图，两座相距60 m的建筑物AB，CD的高度分别为20 m,50 m，BD为水平面，则从建筑物AB的顶端A看建筑物CD的张角∠CAD等于A.30° B.45°C.60° D.75°
又CD＝50 m，所以在△ACD中，由余弦定理得
又0°<∠CAD<180°，所以∠CAD＝45°，所以从建筑物AB的顶端A看建筑物CD的张角∠CAD为45°.
4.如图，航空测量的飞机航线和山顶在同一铅直平面内，已知飞机飞行的海拔高度为10 000 m，速度为50 m/s.某一时刻飞机看山顶的俯角为15°，经过420 s后看山顶的俯角为45°，则山顶的海拔高度大约为(参考数据： )A.7 350 m B.2 650 mC.3 650 m D.4 650 m
如图，设飞机的初始位置为点A，经过420 s后的位置为点B，山顶为点C，作CD⊥AB于点D，则∠BAC＝15°，∠CBD＝45°，所以∠ACB＝30°，在△ABC中，AB＝50×420＝21 000(m)，
所以山顶的海拔高度大约为10 000－7 350＝2 650(m).
5.(2023·洛阳模拟)某班课外学习小组利用“镜面反射法”来测量学校内建筑物的高度.步骤如下：①将镜子(平面镜)置于平地上，人后退至从镜中能看到房顶的位置，测量出人与镜子的距离；②将镜子后移，重复①中的操作；③求建筑物高度.如图所示，前后两次人与镜子的距离分别为a1 m，a2 m(a2>a1)，两次观测时镜子间的距离为a m，人的“眼高”为h m，则建筑物的高度为
设建筑物的高度为x，如图所示，由△HGF∽△DEF，
所以ah＋xa1＝xa2，即x(a2－a1)＝ah，
6.(2023·济南模拟)山东省科技馆新馆目前成为济南科教新地标(如图1)，其主体建筑采用与地形吻合的矩形设计，将数学符号“∞”完美嵌入其中，寓意无限未知、无限发展、无限可能和无限的科技创新.如图2，为了测量科技馆最高点A与其附近一建筑物楼顶B之间的距离，无人机在点C测得点A和点B的俯角分别为75°，30°，随后无人机沿水平方向飞行600米到点D，此时测得点A和点B的俯角分别为45°和60°(A，B，C，D在同一铅垂面内)，则A，B两点之间的距离为
由题意，∠DCB＝30°，∠CDB＝60°，所以∠CBD＝90°，
又∠DCA＝75°，∠CDA＝45°，所以∠CAD＝60°，
在△ABC中，∠ACB＝∠DCA－∠DCB＝75°－30°＝45°，由余弦定理得
A.A处与D处之间的距离是24 n mileB.灯塔C与D处之间的距离是16 n mileC.灯塔C在D处的南偏西30°方向D.D处在灯塔B的北偏西30°方向
所以B＝180°－60°－75°＝45°，
在△ACD中，由余弦定理得
由B项解析知CD＝AC，所以∠CDA＝∠CAD＝30°，所以灯塔C在D处的南偏西30°方向，故C正确；由∠ADB＝60°，得D处在灯塔B的北偏西60°方向，故D错误.
8.(2024·重庆模拟)解放碑是重庆的地标性建筑，众多游客来此打卡拍照.现某中学数学兴趣小组对解放碑的高度进行测量，并绘制出测量方案示意图(如图所示)，A为解放碑的最顶端，B为基座(即B在A的正下方)，在步行街上(与B在同一水平面内)选取C，D两点，测得CD的长为100 m.小组成员利用测角仪已测得∠ACB＝ ，则根据下列各组中的测量数据，能计算出解放碑高度AB的是 A.∠BCD，∠BDC B.∠ACD，∠ADCC.∠BCD，∠ACD D.∠BCD，∠ADC
对于D，由∠ACB，∠BCD借助直角三角形和余弦定理，用AB表示出CB，BD，AC，AD，然后结合∠ADC在△ADC中利用余弦定理列方程，解方程求得AB，故D正确.
三、填空题9.中国最早的天文观测仪器叫“圭表”(如图)，最早装置圭表的观测台是西周初年在阳城建立的周公测景(影)台.“圭”就是放在地面上的土堆，“表”就是直立于圭的杆子，太阳光照射在表上，便在圭上成影.到了周代，使用圭表有了规范，杆子(表)规定为八尺长.用圭表测量太阳照射在竹竿上的影长，可以判断季节的变化，也能用于丈量土地.同一天内，南北两地的日影长短倘使差一寸，它们的距离就相差一千里，所谓“影差一寸，地差千里”(1尺＝10寸).记“表”的顶部为A，太阳光线通过顶部A投影到“圭”上的点为B.同一天内，甲地日影长是乙地日影长的两倍，记甲地中直线AB与地面所成的角为θ，且tan θ＝ .则甲、乙两地之间的距离约为________千里.
则甲、乙两地之间的距离约为(3－1.5)×10＝15(千里).
10.如图所示，工程师为了了解深水港码头海域海底的构造，在海平面内一条直线上的A，B，C三点进行测量.已知AB＝60 m，BC＝120 m，于A处测得水深AD＝120 m，于B处测得水深BE＝200 m，于C处测得水深CF＝150 m，则cs∠DEF＝______.
11.台风中心从A地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地区为危险区，城市B在A的正东方向40千米处，则城市B处于危险区的时间为________小时.
设A地东北方向上存在点P到城市B的距离为30千米，AP＝x，在△ABP中，由余弦定理得PB2＝AP2＋AB2－2AP·AB·cs A，即302＝x2＋402－2x·40·cs 45°，
设方程的两根为x1，x2，
即图中CD＝20千米，
12.汾阳文峰塔建于明末清初，位于山西省汾阳市城区以东2公里的建昌村，该塔共十三层，雄伟挺拔，高度位于中国砖结构古塔之首.如图，某测绘小组为了测量汾阳文峰塔的实际高度AB，选取了与塔底B在同一水平面内的三个测量基点C，D，E，现测得∠BCD＝30°，∠BDC＝70°，∠BED＝120°，BE＝17.2 m，DE＝10.32 m，在点C处测得塔顶A的仰角为62°，则塔高AB＝________ m.(结果精确到1 m，参考数据：tan 62°≈1.88，sin 70°≈0.94， ＝12.04)
由余弦定理得BD2＝BE2＋DE2－2BE·DE·cs∠BED，
＝2×12.04＝24.08(m).在△BCD中，由正弦定理得