2023-2024学年安徽省安庆外国语学校八年级（下）期末数学试卷（含详细答案解析）

这是一份2023-2024学年安徽省安庆外国语学校八年级（下）期末数学试卷（含详细答案解析），共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.要使二次根式 x−5有意义，则x的取值范围是( )
A. x≠5B. x>5C. x≤5D. x≥5
2.下列方程中是一元二次方程是( )
A. ax2+bx+c=0B. x2−8x=7C. x2−1+2x3=0D. x2−4x+4=0
3.在下列四组数中，属于勾股数的是( )
A. 1，2，3B. 1， 2， 3C. 4，5，6D. 5，12，13
4.若一个多边形的每一个外角都等于45∘，则这个多边形是( )
A. 五边形B. 六边形C. 七边形D. 八边形
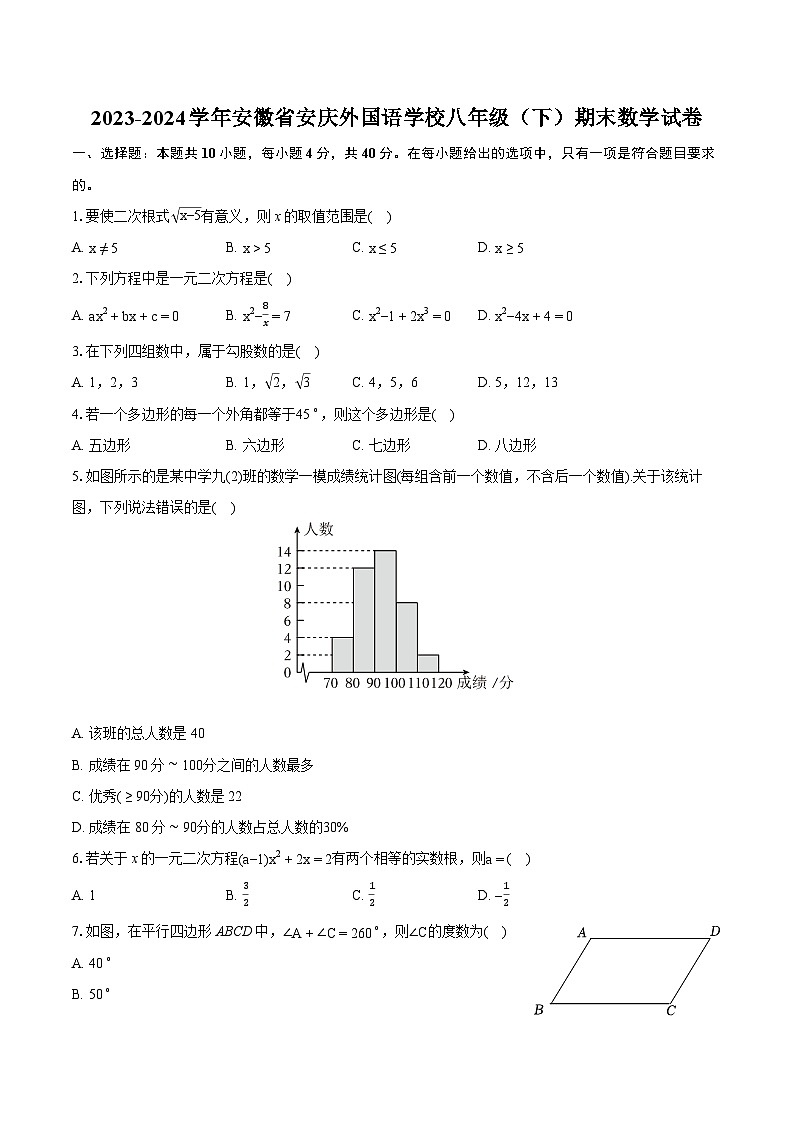
5.如图所示的是某中学九(2)班的数学一模成绩统计图(每组含前一个数值，不含后一个数值).关于该统计图，下列说法错误的是( )
A. 该班的总人数是40
B. 成绩在90分∼100分之间的人数最多
C. 优秀(≥90分)的人数是22
D. 成绩在80分∼90分的人数占总人数的30%
6.若关于x的一元二次方程(a−1)x2+2x=2有两个相等的实数根，则a=( )
A. 1B. 32C. 12D. −12
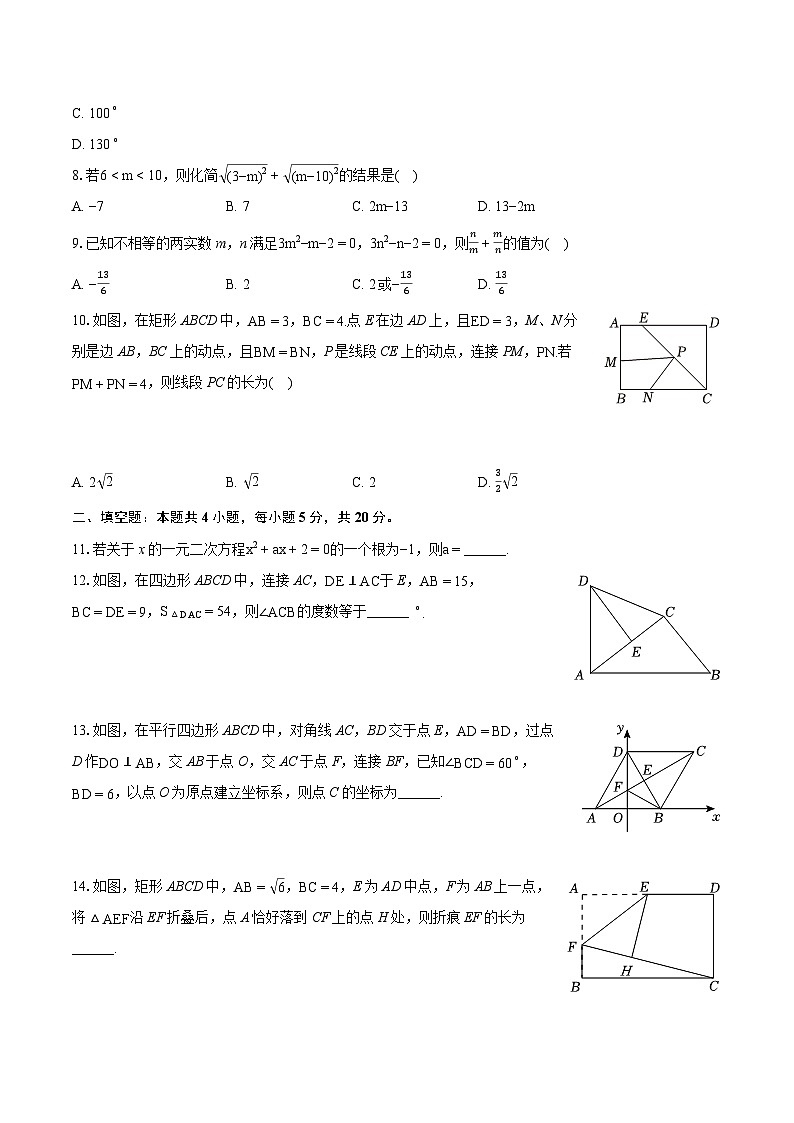
7.如图，在平行四边形ABCD中，∠A+∠C=260∘，则∠C的度数为( )
A. 40∘
B. 50∘
C. 100∘
D. 130∘
8.若6A. −7B. 7C. 2m−13D. 13−2m
9.已知不相等的两实数m，n满足3m2−m−2=0，3n2−n−2=0，则nm+mn的值为( )
A. −136B. 2C. 2或−136D. 136
10.如图，在矩形ABCD中，AB=3，BC=4.点E在边AD上，且ED=3，M、N分别是边AB，BC上的动点，且BM=BN，P是线段CE上的动点，连接PM，PN.若PM+PN=4，则线段PC的长为( )
A. 2 2B. 2C. 2D. 32 2
二、填空题：本题共4小题，每小题5分，共20分。
11.若关于x的一元二次方程x2+ax+2=0的一个根为−1，则a=______.
12.如图，在四边形ABCD中，连接AC，DE⊥AC于E，AB=15，BC=DE=9，S△DAC=54，则∠ACB的度数等于______ ∘.
13.如图，在平行四边形ABCD中，对角线AC，BD交于点E，AD=BD，过点D作DO⊥AB，交AB于点O，交AC于点F，连接BF，已知∠BCD=60∘，BD=6，以点O为原点建立坐标系，则点C的坐标为______.
14.如图，矩形ABCD中，AB= 6，BC=4，E为AD中点，F为AB上一点，将△AEF沿EF折叠后，点A恰好落到CF上的点H处，则折痕EF的长为______.
三、解答题：本题共9小题，共90分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题10分)
计算：(−13)−2+|1−2 2|− 18÷ 2.
16.(本小题10分)
解下列方程：x2−10x+25=2(x−5)
17.(本小题10分)
如图，点D在△ABC中，∠BDC=90∘，AB=13，AC=12，BD=4，CD=3，求图中阴影部分的面积.
18.(本小题10分)
如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别为A(−2,3)，B(−3,1)，C(0,−2).
(1)将△ABC向右平移5个单位长度后得到△A1B1C1，请画出△A1B1C1；
(2)在平移的过程中，求△ABC扫过的面积.
19.(本小题10分)
观察下列等式，解答后面的问题.
第1个等式： 8+1=3；
第2个等式： 12+12=5 12；
第3个等式： 16+13=7 13；
第4个等式： 20+14=9 14.
…
(1)按照此规律，第5个等式是：______；
(2)写出你猜想的第n个等式(用含n的式子表示)，并证明.
20.(本小题10分)
随机抽取部分八年级学生，调查每个月的零花钱消费额，数据整理成如下的统计表和统计图.已知图1中，A，E两组对应的小长方形高度之比为2：1.m为B组所占的百分率
请回答以下问题
(1)本次调查样本的容量是______；m=______.
(2)补全频数分布直方图，并在图中标明各组的频数；
(3)若该校有2000名学生，试估计月消费零花钱不少于300元的学生的数量.
21.(本小题10分)
如图，在平行四边形ABCD中，对角线AC的垂直平分线EF与BC相交于点E，与AD相交于点F，连接AE，CF.
(1)求证：四边形AECF是菱形；
(2)若四边形AECF的周长为20，S四边形ABEF=24，求四边形AECF的对角线之和？
22.(本小题10分)
某农户种植花生，原来花生的亩产量为200千克，出油率为50%(即每100千克花生可加工成花生油50千克)，现在种植新品种花生后，每亩收获的花生可加工成花生油132千克，其中花生出油率的增长率是亩产量的增长率的12.求新品种花生亩产量的增长率.
(1)这是一个增长率问题，可设所求增长率为x，依题意填写下列表格：
(2)求新品种花生亩产量的增长率.
23.(本小题10分)
如图，菱形ABCD的对角线AC，BD相交于点O，且∠ABC=60∘，AB=6.
(1)求BD的长；
(2)点E在线段BD上，且AE⊥AB，点F为线段BC上一动点.
①当BF=2时，求四边形DEFC的面积；
②记2EF+BF的最小值为a，OF+AF的最小值为b.求a2−b2的值.
答案和解析
1.【答案】D
【解析】【分析】
本题考查了二次根式有意义的条件，掌握二次根式的被开方数是非负数是解题的关键．
根据二次根式的被开方数是非负数即可得出答案．
【解答】
解：∵x−5≥0，
∴x≥5.
故选：D.
2.【答案】D
【解析】解：A、当a=0时，该方程不含有二次项，则它不是一元二次方程，不符合题意；
B、该方程不是整式方程，不符合题意；
C、该方程中未知数x的最高次数是3，则它不是一元二次方程，不符合题意；
D、该方程符合一元二次方程的定义，符合题意．
故选：D.
利用一元二次方程的定义：含有一个未知数，且未知数的最高次数为2次，这样的整式方程，判断即可．
此题考查了一元二次方程的定义，熟练掌握一元二次方程的定义是解本题的关键．
3.【答案】D
【解析】解：A、1+2=3，不能构成三角形，不符合题意；
B、 2， 3不是整数，故不是勾股数，不符合题意；
C、42+52≠62，故不是勾股数，不符合题意；
D、52+122=132，故是勾股数，符合题意；
故选：D.
根据勾股数就是可以构成一个直角三角形三边的一组正整数，根据勾股数的定义逐项判断即可．
本题考查了勾股数的定义，熟练掌握勾股数的定义是解此题的关键．
4.【答案】D
【解析】【分析】
此题主要考查了多边形的外角和，解题的关键是掌握多边形的外角和为360∘是解题关键．
根据多边形每一个外角都是45∘，利用外角和除以外角的度数可得多边形的边数．
【解答】
解：多边形的边数为360÷45=8，
所以这个多边形是八边形，
故选：D.
5.【答案】C
【解析】解：A.该班的总人数是2+4+8+12+14=40，故A选项说法正确，不符合题意；
B.由统计图可知，成绩在90分∼100分之间的人数是14，是最多的，故B选项说法正确，不符合题意；
C.优秀(≥90分)的人数是14+8+2=24，故C选项说法错误，符合题意；
D.成绩在80∼90分的人数是12，占总人数的1240×100%=30%，故D选项说法正确，不符合题意．
故选：C.
根据从直方图上获取的信息逐项判断即可解答．
本题主要考查了频数分布直方图，从直方图上获得所需信息是解题的关键．
6.【答案】C
【解析】解：∵(a−1)x2+2x=2，
∴(a−1)x2+2x−2=0，
根据题意得a−1≠0且Δ=22−4(a−1)×(−2)=0，
解得a=12.
故选：C.
根据一元二次方程根的判别式的意义得到a−1≠0且Δ=22−4(a−1)×(−2)=0，然后解一次方程可得到a的值．
本题考查了根的判别式：一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2−4ac有如下关系：当Δ>0时，方程有两个不相等的实数根；当Δ=0时，方程有两个相等的实数根；当Δ<0时，方程无实数根．
7.【答案】D
【解析】解：∵四边形ABCD是平行四边形，
∴∠A=∠C，
∵∠A+∠C=260∘，
∴∠A+∠A=260∘，
∴∠A=130∘，
故选：D.
由平行四边形的性质得∠A=∠C，而∠A+∠C=260∘，则∠A+∠A=260∘，求得∠A=130∘，于是得到问题的答案．
此题重点考查平行四边形的性质、四边形的内角和等于360∘等知识，证明∠A=∠C是解题的关键．
8.【答案】B
【解析】解：∵6∴3−m<0，m−10<0，
∴ (3−m)2+ (m−10)2
=m−3+10−m，
=m−m+10−3
=7，
故选：B.
先根据已知条件，判断3−m和m−10的正负，然后根据二次根式的性质进行计算即可．
本题主要考查了二次根式的性质与化简，解题关键是熟练掌握二次根式的性质．
9.【答案】A
【解析】解：∵不相等的两实数m，n满足3m2−m−2=0，3n2−n−2=0，
∴m、n是方程3x2−x−2=0的两个不相等的实数根，
∴m+n=13，mn=−23，
∴nm+mn=m2+n2mn=(m+n)2−2mnmn=19+43−23=−136.
故选：A.
由已知得m、n是方程3x2−x−2=0的两个不相等的实数根，根据根与系数的关系即可得出m+n=13，mn=−23，把要求的式子化简再代入m+n=13，mn=−23，即可求出答案．
本题考查了根与系数的关系，分式的化简求值，若x1，x2是一元二次方程ax2+bx+c=0(a≠0)的两根时，x1+x2=−ba，x1⋅x2=ca.
10.【答案】A
【解析】解：∵矩形ABCD，
∴CD=AB=3，∠ADC=90∘，
∵ED=3=CD，
∴∠DCE=45∘，
∴∠BCE=45∘，
如图1，在CD上取点N，使CN′=CN，连接PN′，MN′，
∴PM+PN=PM+PN′=4，
∵PM+PN′>MN′，MN′≥4，
∴MN=4，
∴MN′//BC，
即M、P、N三点共线，
如图2，则四边形BCNM是矩形，
∴BM=CN′，∠CPN′=45∘=∠PCN′，
∴PN′=CN′=CN=BM=BN，
∵CN+BN=4，
∴CN=BN=2，PN′=CN′=CN=2，
由勾股定理得PC= PN2+CN*=2 2，
故选：A.
由题意知，ED=3=CD，则∠DCE=45∘，∠BCE=45∘，如图1，在CD上取点N′，使CN′=CN，连接PN′，MN′，则PM+PN=PM+PN′=4，由PM+PN′>MN，MN′≥4，可得MN′=4，MN′//BC，即 M、P、N′三点共线，如图2，则四边形BCN′M是矩形，则PN′=CN′=CN=BM=BN，由CN+BN=4，可求PN′=CN′=CN=2，由勾股定理得PC= PN′2+CN′2，计算求解即可．
本题考查了等腰三角形的判定与性质，矩形的判定与性质，三角形三边关系，勾股定理等知识．明确PM+PN=4时，点P的位置是解题的关键．
11.【答案】3
【解析】解：∵关于x的一元二次方程x2+ax+2=0的一个根为−1，
∴将x=−1代入原方程得：(−1)2−a+2=0，
解得：a=3，
故答案为：3.
将x=−1代入原方程即可解出a的值．
本题考查一元二次方程的解，代入求值是关键．
12.【答案】90
【解析】解：∵DE⊥AC，
∴S△DAC=12AC⋅DE=54，
∵DE=9，
∴12×9×AC=54，
解得：AC=12，
∵AC=12，BC=9，AB=15，
∴AC2+BC2=AB2，
∴∠ACB=90∘，
故答案为：90.
先根据S△DAC=54，求出AC=12，再根据“两边平方和等于第三边平方的三角形是直角三角形”，即可得出结论．
本题考查了勾股定理，三角形的面积，关键是三角形面积公式的应用．
13.【答案】(6,3 3)
【解析】解：∵四边形ABCD为平行四边形，
∴AB=CD，∠BCD=∠BAD=60∘.
∵AD=BD，
∴△ABD为等边三角形．
∴AD=BD=AB=6，DO为AB边上的中线．
∴AO=BO=3.
在Rt△AOD中，由勾股定理得，OD= AD2−AO2=3 3，
∵CD=AB=6，
∴点C的坐标为(6,3 3).
故答案为：(6,3 3).
根据平行四边形的性质结合AD=BD，可得△ABD为等边三角形．从而得到AO=BO=3，在Rt△AOD中，由勾股定理可得OD的长，即可．
本题主要考查了平行四边形的性质，坐标与图形，平行四边形的性质，勾股定理，等边三角形的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
14.【答案】2 153
【解析】解：如图所示，连接CE，
∵E为AD中点，
∴AE=DE=2，
由折叠可得，AE=GE，∠EGF=∠A=90∘，
∴DE=GE，
又∵∠D=90∘，
∴∠EGC=∠D=90∘，
又∵CE=CE，
∴Rt△CDE≌Rt△CGE(HL)，
∴CD=CG= 6，
设AF=x，则GF=x，BF= 6−x，CF= 6+x，
∵∠B=90∘，
∴Rt△BCF中，BF2+BC2=CF2，
即( 6−x)2+42=(x+ 6)2，
解得x=2 63，
∴AF=2 63，
∵∠A=90∘，
∴Rt△AEF中，EF= AE2+AF2= 22+(2 63)2=2 153，
故答案为：2 153.
连接EC，利用矩形的性质以及折叠的性质，即可得到△CDE与△CGE全等，设AF=x，则可得CF=x+ 6，BF= 6−x，在Rt△BCF中利用勾股定理即可得到x的值，在Rt△AEF中利用勾股定理即可求出EF的长度．
本题主要考查了矩形的性质以及折叠问题，解题时我们常常设要求的线段长为x，然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．
15.【答案】解：(−13)−2+|1−2 2|− 18÷ 2
=9+2 2−1−3
=5+2 2.
【解析】先计算负整数指数幂、绝对值和二次根式，再计算加减．
此题考查了实数的混合运算能力，关键是能准确确定运算顺序和方法，并能进行正确地计算．
16.【答案】解：x2−10x+25=2(x−5)，
(x−5)2−2(x−5)=0，
(x−5)(x−5−2)=0，
x−5=0，x−5−2=0，
x1=5，x2=7.
【解析】移项后分解因式，即可得出两个一元一次方程，求出方程的解即可．
本题考查了解一元二次方程，能把一元二次方程转化成一元一次方程是解此题的关键．
17.【答案】解：∵∠BDC=90∘，BD=4，CD=3，
∴BC= BD2+CD2= 42+32=5，
∵AB=13，AC=12，
∴AC2+BC2=122+52=169，AB2=132=169，
∴AC2+BC2=AB2，
∴△ABC是直角三角形，
∴∠ACB=90∘，
∴图中阴影部分的面积=△ABC的面积−△BDC的面积
=12AC⋅BC−12BD⋅CD
=12×12×5−12×3×4
=30−6
=24，
∴图中阴影部分的面积为24.
【解析】先在Rt△BDC中，利用勾股定理求出BC=5，然后利用勾股定理的逆定理证明△ABC是直角三角形，从而可得∠ACB=90∘，最后根据图中阴影部分的面积=△ABC的面积−△BDC的面积，进行计算即可解答．
本题考查了勾股定理的逆定理，勾股定理，熟练掌握勾股定理的逆定理，以及勾股定理是解题的关键．
18.【答案】解：(1)如图，△A1B1C1即为所求．
(2)在平移的过程中，△ABC扫过的面积为S△ABC+S四边形ACC1A1=12×(1+3)×5−12×3×3−12×1×2+5×5=10−92−1+25=592.
【解析】(1)根据平移的性质作图即可．
(2)求出△ABC与四边形ACC1A1的面积之和即可．
本题考查作图-平移变换，熟练掌握平移的性质是解答本题的关键．
19.【答案】 24+15=11 15
【解析】(1)解：根据规律可知，第5个等式是：
24+15=11 15，
故答案为： 24+15=11 15；
(2)根据规律猜想第n个等式为： 4(n+1)+1n=(2n+1) 1n，
证明： 4(n+1)+1n
= 4n(n+1)+1n
= 4n2+4n+1n
= (2n+1)2n
=(2n+1) 1n，
故猜想成立，即 4(n+1)+1n=(2n+1) 1n.
(1)根据规律可知，第5个等式：左边的被开方数是24+15，右边根号外的系数为11，被开方数为15，据此写出第5个等式即可；
(2)根据规律可知，等式左边的被开方数为4(n+1)+1n，等式的右边根号外的系数为(2n+1)，被开方数为 1n，然后证明即可．
本题考查了算术平方根，数字的变化规律，观察所给的式子，找出变化规律是解题的关键．
20.【答案】10020%
【解析】解：(1)本次调查样本的容量是40÷40%=100.
∵A，E两组对应的小长方形高度之比为2：1，A组的频数为10，
∴E组的频数为5，
∴B组的频数为100−10−40−25−5=20，
∴m=20÷100×100%=20%.
故答案为：100；20%.
(2)补全频数分布直方图如图1所示．
(3)2000×25+5100=600(人).
∴估计月消费零花钱不少于300元的学生约600人．
(1)用频数分布直方图中C的频数除以扇形统计图中C的百分比可得本次调查样本的容量；由题意可得E组的频数为5，进而可得B组的频数，用B组的频数除以样本容量再乘以100%可得m的值．
(2)根据(1)所求数据补全频数分布直方图即可．
(3)根据用样本估计总体，用2000乘以样本中D，E组的人数所占的百分比，即可得出答案．
本题考查频数(率)分布直方图、总体、个体、样本、样本容量、频数(率)分布表、用样本估计总体，能够读懂统计图表，掌握用样本估计总体、样本容量的定义是解答本题的关键．
21.【答案】(1)证明：设AC，EF交于点O，
∵EF是AC的垂直平分线，
∴AF=CF，AE=CE，OA=OC，
∵四边形ABCD是平行四边形，
∴AD//BC，
∴∠ACE=∠CAF，∠AFE=∠CEF，
∴△AOF≌△COE(AAS)，
∴AF=CE，
∴AF=CF=CE=AE，
∴四边形AECF是菱形；
(2)解：如(1)图，
∵四边形AECF是菱形，
∴AC⊥EF，AO=CO，EO=FO，
∵菱形AECF的周长为20，
∴AF=5，
∴AO2+OF2=25，
∴(AO+OF)2=25+2AO⋅OF，
∵S四边形ABEF=12AC⋅BD=24，
∴AO⋅OF=12，
∴(AO+OF)2=49，
∴AO+OF=7(负值舍去)，
∴四边形AECF的对角线之和14.
【解析】(1)设AC，EF交于点O，根据线段垂直平分线的性质，可得AF=CF，AE=CE，OA=OC，由“AAS”可证△AOF≌△COE，则可得AF=CE，继而证得结论；
(2)由四边形AECF是菱形，可得AC⊥EF，AO=CO，EO=FO，根据菱形AECF的周长为20，S四边形ABEF=24，根据勾股定理完全平方公式即可得到结论．
本题考查平行四边形的性质和判定，菱形的判定与性质，垂直平分线的性质，勾股定理，三角形全等的判定与性质，证明三角形全等时解题的关键．
22.【答案】解：(1)花生的现在亩产量200(1+x)，花生的现在出油率50%(1+12x)；
(2)设新品种花生亩产量的增长率为x.
200(1+x)×50%(1+12x)=132
x1=15，x2=−165(舍去).
x=15=20%.
故新品种花生亩产量的增长率为20%.
【解析】(1)增长后的量=增长前的量×(1+增长率).
(2)每亩收获的花生可加工成花生油的质量是200(1+x)⋅50%(1+12x)，依此即可列方程求解．
本题考查的是增长率问题，首先表示新植花生的亩产量，再表示出出油率增长后出的油，然后列方程求解．
23.【答案】解：(1)四边形ABCD是菱形，且∠ABC=60∘，AB=6，
∴AC⊥BD，OA=OC=12AC，OB=OD=12BD，
∠OBC=∠OBA=12∠ABC=30∘，
在Rt△ABO中，∠OBA=30∘
∴OA=12AB=3，
∴OB= AB2−OA2=3 3.
∴BD=2OB=6 3.
(2)①如图，连接CE，设AE=x，
∵AE⊥AB，
∴∠BAE=90∘.
在Rt△ABE中，∠EBA=30∘，
BE=2AE=2x，
AE2+AB2=BE2，
即x2+62=(2x)2，
解得：x1=−2 3(舍)，x2=2 3.
∴AE=2 3.
在△ABE和△CBE中，
AB=CB,∠ABE=∠CBE,BE=BE,
∴△ABE≌△CBE(SAS).
∴CE=AE=2 3，∠BCE=∠BAE=90∘.
S△BEF=12BF⋅CE=12×2×2 3=2 3.
S△BCD=12BD⋅OC=12×6 3×3=9 3.
∴S四形DEFC=S△BCD−S△BEF=9 3−2 3=7 3.
∴四边形DEFC的面积是7 3.
②如图，过点B作BH⊥AB，且BH=OB，过点F作FG⊥BH于点G，连接FH.
∵BH⊥AB，FG⊥BH，
∴∠ABH=∠BGF=90∘，
∴∠CBH=∠ABH−∠ABC=90∘−60∘=30∘，
在Rt△BFG中，FG=12BF.
∴2EF+BF=2(EF+12BF)=2(EF+FG)≥2EG.
∴当E、F、G共线时，2EF+BF的值最小，此时∠EGB=90∘.
∴∠EGB=∠ABG=∠BAE=90∘，
∴四边形ABGE是矩形．
∴EG=AB=6.
∴a=(2EF+BF)=2EG=12.
在△OBF和△HBF中，
OB=HB,∠OBF=∠HBF,BF=BF
∴△OBF≌△HBF(SAS).
∴FH=OF，
∴OF+AF=HF+AF≥AH.
∴当A、F、H共线时，OF+AF的值最小．
在Rt△ABH中，
AH= AB2+BH2= 36+27=3 7.
∴b=AH=3 7.
∴a2−b2=122−63=81.
∴a2−b2的值为81.
【解析】(1)根据四边形ABCD是菱形，且∠ABC=60∘，AB=6，得出AC⊥BD，OA=OC=12AC，0B=0D=12BD，∠OBC=∠OBA=30∘.在RtABO中，根据直角三角形的性质得出OA=3，再根据勾股定理算出OB=3 3，即可解答．
(2)①如图，连接CE，设AE=x，在Rt△ABE中，根据∠EBA=30∘，得出BE=2AE=2x，根据勾股定理即可解出，AE=2 3.证明△ABE≌△CBE(SAS)，即可得出CE=AE=2 3，∠BCE=∠BAE=90∘.算出S△BEF，S△BCD，再根据S四边形DEFC=S△BCD−S△BEF即可计算．
②如图，过点B作BH⊥AB，且BH=OB，过点F作FG⊥BH于点G，连接FH、证出∠CBH=30∘，在Rt△BFG中，根据直角三角形的性质得出FG=12BF，根据2EF+BF=2(EF+FG)>2EG，得出当E、F、G共线时，2EF+BF的值最小，此时∠EGB=90∘，证出四边形ABGE是矩形，即可得出EG=AB=6，a=(2EF+BF)=12.证明△OBF≌△HBF(SAS)，得出FH=OF，得出当A、F、H共线时，OF+AF的值最小，在Rt△ABH中，根据定理得出AH=37，即可算出b，即可解答．
该题主要考查了全等三角形的性质和判定，菱形的性质，矩形的性质和判定，勾股定理，解题的关键是掌握以上知识点．组别
月零花钱消费额/元
A
10≤x<100
B
100≤x<200
C
200≤x<300
D
300≤x<400
E
x≥400
亩产量(千克)
出油率(%)
出油量(千克)
原来
200
50
200×50
现在
132