2023-2024学年安徽省安庆市太湖县八年级（下）期末数学试卷（含详细答案解析）

这是一份2023-2024学年安徽省安庆市太湖县八年级（下）期末数学试卷（含详细答案解析），共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.下列是最简二次根式的是( )
A. 12B. 10C. 8D. 12
2.若m是关于x的方程x2−2024x−1=0的根，则(m2−2024m−4)(m2−2024m+4)的值为( )
A. −15B. 15C. −16D. 16
3.某篮球队10名队员的年龄如表所示：
则这10名队员年龄的众数和中位数分别是( )
A. 19岁、19岁B. 19岁、19.5岁C. 20岁、19岁D. 20岁、19.5岁
4.如图，在3×3的正方形网格中，若小正方形的边长是1，则任意两个格点间的距离不可能是( )
A. 6
B. 8
C. 9
D. 13
5.关于x的一元二次方程(m−5)x2+2x+2=0有实数根，则m的最大整数解是( )
A. 2B. 3C. 4D. 5
6.下列各组线段能构成直角三角形的是( )
A. 1，1，2B. 3,2, 5C. 7，12，13D. 3,4, 7
7.若x1，x2是方程x2−2x−1=0的两个根，则2x1+2x2−x1x2的值为( )
A. 5B. −5C. 3D. −3
8.下列正多边形的组合中，不能够铺满地面的是( )
A. 正三角形和正方形B. 正三角形和正六边形
C. 正方形和正六边形D. 正方形和正八边形
9.今年“国庆节”和“中秋节”双节期间，某微信群规定，群内的每个人都要发一个红包，并保证群内其他人都能抢到且自己不能抢自己发的红包，若此次抢红包活动，群内所有人共收到90个红包，则该群一共有( )
A. 9人B. 10人C. 11人D. 12人
10.如图，在正方形ABCD中，AB=3，点EF分别在CD，AD上，CE=DF，BE，CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2：3，则△BCG的周长为( )
A. 7
B. 3+ 13
C. 8
D. 3+ 15
二、填空题：本题共4小题，每小题5分，共20分。
11.若某多边形从一个顶点所作的对角线为4条，则这个多边形共有______条对角线.
12.若013.小强问他的数学老师今年多少岁了，数学老师说：“我像你这么大时，你才1岁.你到我这么大时，我就40岁了.”那么数学老师今年的岁数是______岁.
14.如图，在正方形ABCD中，连接对角线AC，F在线段BE上，连接AF交BC于点G，∠BEC=2∠AFB，EF=1，CE=3，则CG=______.
三、解答题：本题共9小题，共90分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题8分)
计算：| 2−2|−12×(−13)+ 183.
16.(本小题8分)
用配方法解方程，2x2+5x−12=0.
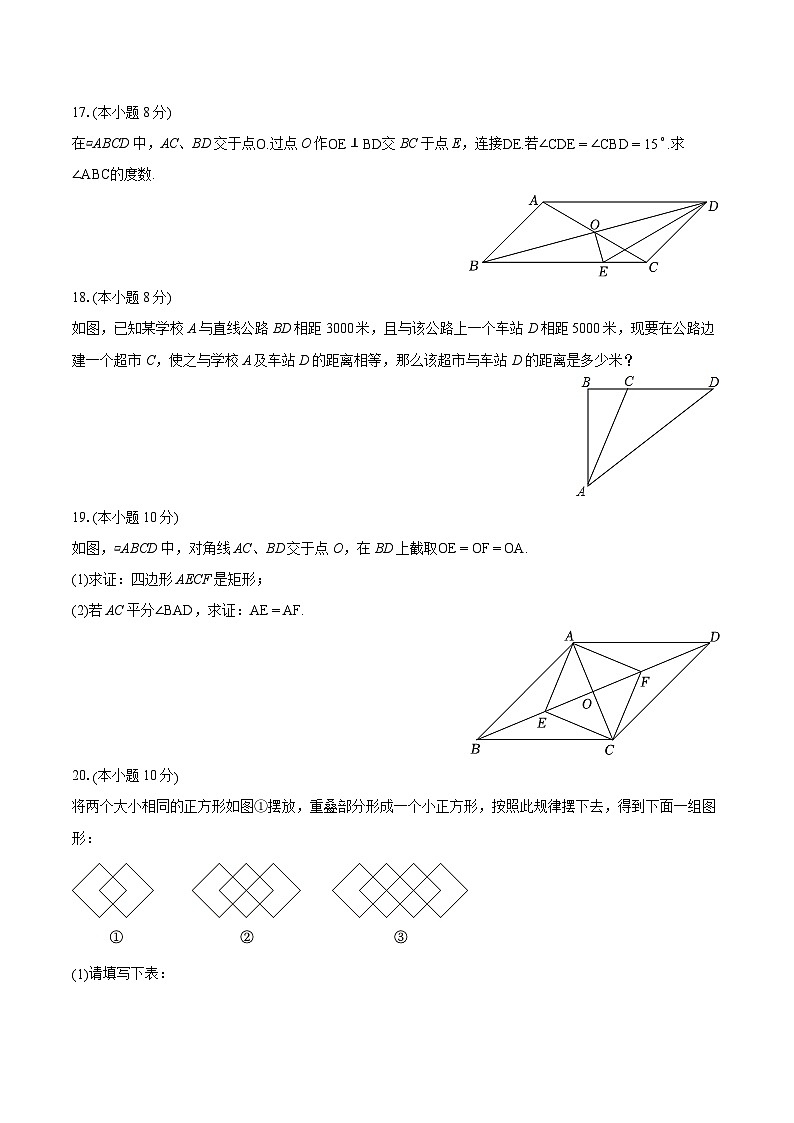
17.(本小题8分)
在▱ABCD中，AC、BD交于点O.过点O作OE⊥BD交BC于点E，连接DE.若∠CDE=∠CBD=15∘.求∠ABC的度数.
18.(本小题8分)
如图，已知某学校A与直线公路BD相距3000米，且与该公路上一个车站D相距5000米，现要在公路边建一个超市C，使之与学校A及车站D的距离相等，那么该超市与车站D的距离是多少米？
19.(本小题10分)
如图，▱ABCD中，对角线AC、BD交于点O，在BD上截取OE=OF=OA.
(1)求证：四边形AECF是矩形；
(2)若AC平分∠BAD，求证：AE=AF.
20.(本小题10分)
将两个大小相同的正方形如图①摆放，重叠部分形成一个小正方形，按照此规律摆下去，得到下面一组图形：
(1)请填写下表：
(2)第100个图形中，有______个正方形；若第 n个图形中小正方形的个数是大正方形的2倍，则n=______；
(3)是否存在一个图形，这个图形中小正方形的个数是大正方形个数的平方？如果存在，求出图形的编号；如果不存在，请说明理由.
21.(本小题12分)
某校开展了以“养成读书好习惯”为主题的读书活动.学校对部分学生四月份读书量进行了随机抽样调查，读书量为2本书的占30%，并对所有随机抽取学生的“读书量”(单位：本)进行了统计，如图所示，根据以上信息，解答下列问题：
(1)一共抽取了______名学生；
(2)补全条形统计图；
(3)样本的众数是______本；
(4)已知该校有1200名学生，请你估计该校学生中，四月份“读书量”为5本的学生人数.
22.(本小题12分)
读下列材料：已知实数m，n满足(2m2+n2+1)(2m2+n2−1)=80，试求2m2+n2的值.
解：设2m2+n2=t，则原方程变为(t+1)(t−1)=80，整理得t2−1=80，t2=81，
∴t=±9，∵2m2+n2≥0，∴2m2+n2=9，
上面这种方法称为“换元法”，在结构较复杂的数和式的运算中，若把其中某些部分看成一个整体，并用新字母代替(即换元)，则能使复杂的问题简单化.
根据以上阅读材料内容，解决下列问题，并写出解答过程.
(1)设a，b满足等式(a2+b2)(2a2+2b2−1)=3，求3a2+3b2−1的值；
(2)若四个连续正整数的积为24，求这四个连续正整数.
23.(本小题14分)
(1)【教材呈现】以下是华师版八年级下册数学教材第117页的部分内容：
例：如图，已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F.求证：四边形AFCE是菱形．
分析：要证四边形AFCE是菱形，由已知条件可知EF⊥AC，所以只需证明四边形AFCE是平行四边形，又知EF垂直平分AC，所以只需证明OE=OF.
请结合图1，补全证明过程．
(2)【应用】如图2，将矩形ABCD沿直线EF翻折，使点C的对称点与点A重合，点D的对称点为D′，直线EF分别交矩形ABCD的边AD、BC于点E、F，若AB=6，BC=8，则折痕EF的长为______.
(3)【拓展】如图3，将平行四边形ABCD沿直线EF翻折，使点C的对称点与点A重合，点D的对称点为D′，直线EF分别交平行四边形ABCD的边AD、BC于点E、F，若AB= 2，BC=2，∠BCD=45∘，则四边形AFCE的面积是______.
答案和解析
1.【答案】B
【解析】解：A， 12= 22，因此 12不是最简二次根式，不符合题意；
B， 10是最简二次根式，符合题意；
C， 8=2 2，因此 8不是最简二次根式，不符合题意；
D， 12=2 3，因此 12不是最简二次根式，不符合题意．
故选：B.
最简二次根式需满足：被开方数不含分母，被开方数中不含能开得尽方的因数或因式，逐一进行判断即可得出答案．
本题考查最简二次根式的判断，掌握被开方数不含分母，被开方数中不含能开得尽方的因数或因式是关键．
2.【答案】A
【解析】解：根据题意可得：m2−2024m−1=0，
∴m2−2024m=1，
∴(m2−2024m−4)(m2−2024m+4)
=(1−4)(1+4)
=−3×5
=−15.
故选：A.
根据一元二次方程的解的定义得到m2−2024m−1=0，变形得出m2−2024m=1，然后整体代入的方法计算即可．
本题主要考查了一元二次方程的解以及代数式求值，熟练掌握一元二次方程定义是关键．
3.【答案】A
【解析】解：19出现4次，次数最多，故众数为19，
数据按照从小到大或从大到小排列后，第5和第6个数据都是19，故中位数是19岁，
故选：A.
根据中位数与众数的定义求解即可．
本题考查了中位数与众数的定义，掌握中位数与众数的定义是解题的关键．中位数：把一组数据按从小到大的顺序排列，在最中间的一个数字(或者两个数字的平均值)叫做这组数据的中位数．众数：在一组数据中出现次数最多的数．
4.【答案】A
【解析】解：∵在3×3的正方形网格中，若小正方形的边长是1，
∴任意两个格点间的距离为 22+22= 8， 32+12= 10， 9=3，
32+32=3 2， 22+12= 5， 22+32= 13.
∴任意两个格点间的距离不可能是 6，
故选：A.
利用直角三角形的勾股定理即可求出答案．
本题主要考查了勾股定理，在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
5.【答案】C
【解析】【分析】
本题考查了根的判别式，一元二次方程的定义，能得出关于m的不等式是解此题的关键．
根据方程有实数根得出△≥0，根据一元二次方程的定义得到m−5≠0，求出不等式的解集即可．
【解答】
解：∵关于x的一元二次方程(m−5)x2+2x+2=0有实根，
∴△=22−4(m−5)×2≥0且m−5≠0，
解得：m≤5.5且m≠5，
m的最大整数解为4，
故选C.
6.【答案】D
【解析】解：A、1+1=2，不能构成三角形，故不符合题意；
B、( 3)2+22≠( 5)2，不符合勾股定理的逆定理，不能构成直角三角形，故不符合题意；
C、72+122≠132，不符合勾股定理的逆定理，不能组构成直角三角形，故不符合题意；
D、32+( 7)2=42，符合勾股定理的逆定理，能构成直角三角形，故符合题意．
故选：D.
根据勾股定理的逆定理可知，当三角形中三边的关系为：a2+b2=c2时，则三角形为直角三角形．
此题考查的是勾股定理的逆定理，熟知如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形是解题的关键．
7.【答案】A
【解析】解：因为x1，x2是方程x2−2x−1=0的两个根，
所以x1+x2=−−21=2，x1x2=−11=−1，
所以2x1+2x2−x1x2=2(x1+x2)−x1x2=2×2−(−1)=5.
故选：A.
利用一元二次方程根与系数的关系结合整体思想即可解决问题．
本题考查根与系数的关系，熟知一元二次方程根与系数的关系是解题的关键．
8.【答案】C
【解析】解：A、正三角形、正方形内角分别为60∘、90∘，由于60×3+90×2=360，故能铺满，选项不符合题意；
B、正六边形和正三角形内角分别为120∘、60∘，由于60×4+120=360，故能铺满，选项不符合题意；
C、正方形和正六边形内角分别是90∘、120∘，90m+120n=360∘，m=4−43n，显然n取任何正整数时，m不能得正整数，故不能够进行镶嵌，选项符合题意．
D、正八边形和正方形内角分别为135∘、90∘，由于135×2+90=360，故能铺满，选项不符合题意．
故选：C.
正多边形的组合能否铺满地面，关键是看位于同一顶点处的几个角之和能否为360∘.若能，则说明能铺满；反之，则说明不能铺满．
本题考查了平面镶嵌，解决此类题，可以记住几个常用正多边形的内角，及能够用两种正多边形镶嵌的几个组合．
9.【答案】B
【解析】解：设该群共有x人，
依题意有x(x−1)=90，
解得：x=−9(舍去)或x=10，
答：这个群共有10人．
故选：B.
设该群的人数是x人，则每个人要发其他(x−1)张红包，则共有x(x−1)张红包，等于90个，由此可列方程．
本题考查的是一元二次方程在实际生活中的应用，正确找准等量关系列方程即可，比较简单．
10.【答案】D
【解析】解：∵阴影部分的面积与正方形ABCD的面积之比为2：3，
∴阴影部分的面积为23×9=6，
∴空白部分的面积为9−6=3，
由CE=DF，BC=CD，∠BCE=∠CDF=90∘，可得△BCE≌△CDF，
∴△BCG的面积与四边形DEGF的面积相等，均为12×3=32，
∠CBE=∠DCF，
∵∠DCF+∠BCG=90∘，
∴∠CBG+∠BCG=90∘，即∠BGC=90∘，
设BG=a，CG=b，则12ab=32，
又∵a2+b2=32，
∴a2+2ab+b2=9+6=15，
即(a+b)2=15，
∴a+b= 15，即BG+CG= 15，
∴△BCG的周长= 15+3，
故选：D.
根据阴影部分的面积与正方形ABCD的面积之比为2：3，得出阴影部分的面积为6，空白部分的面积为3，进而依据△BCG的面积以及勾股定理，得出BG+CG的长，进而得出其周长．
此题考查了全等三角形的判定与性质、正方形的性质以及三角形面积问题．解题时注意数形结合思想与方程思想的应用．
11.【答案】14
【解析】解：∵从某个多边形的一个顶点出发一共画出4条对角线，
∴n−3=4，
∴n=7，
那么这个多边形对角线的总条数为：12×7×(7−3)=14.
故答案为：14.
根据对角线的概念，知一个多边形从一个顶点出发有(n−3)条对角线，求出n的值，再根据多边形对角线的总数为12n(n−3)，即可解答．
本题考查了多边形的对角线，解决本题的关键是熟记对角线的有关概念．
12.【答案】2x
【解析】解：原式= (x+1x)2− (x−1x)2
=x+1x−(1x−x)=2x.
由(x−1x)2+4=(x+1x)2，(x+1x)2−4=(x−1x)2，又00，通过变形化简原式即可得出最终结果．
本题考查的是对完全平方公式的灵活使用和对二次根式的化简应用．
13.【答案】27
【解析】解：设数学老师今年的岁数是x岁，则小强今年的岁数是x−(40−x)=(2x−40)岁，
根据题意得：2x−40−1=40−x，
解得：x=27，
∴数学老师今年的岁数是27岁．
故答案为：27.
设数学老师今年的岁数是x岁，则小强今年的岁数是(2x−40)岁，根据小强与数学老师的年龄差不变，可列出关于x的一元一次方程，解之即可得出结论．
本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．
14.【答案】2
【解析】解：延长AF，DE交于一点H，如图所示：
，
由图可得：∠AFB=∠HFE，
∵∠BEC=2∠AFB，
∴∠BEC=2∠HFE，
∵∠BEC=∠HFE+∠FHE，
∴∠HFE=∠FHE=∠AFB，
∵EF=1，
∴EH=EF=1，
∵CE=3，
∴CH=CE+EH=3+1=4，
∵ABCD为正方形，
∴AB//DH，
∴∠BAH=∠FHE，
即∠BAH=∠AFB，
∴AB=BF，
设正方形ABCD边长为x，
则BC=x，AB=BF=x，
BE=BF+FE=x+1，
∵△BCE为直角三角形，
∴BE2=CE2+BC2，即(x+1)2=x2+32，
解得：x=4，
在△ABG和△HCG中，
∠ABG=∠HCG=90∘AB=CH∠BAG=∠FHE，
∴△ABG≌△HCG(ASA)，
∴CG=BG=2，
故答案为：2.
先添加辅助线，根据对顶角相等以及三角形的外角的性质，可以得到CH的边长，再根据正方形对边平行，可得到△BAF为等腰三角形，设出正方形的边长，根据勾股定理可以求出边长，再判定两个三角形全等，即可得到结果．
本题考查了正方形的性质、勾股定理、全等三角形的判定及性质、等腰三角形的性质，添加辅助线是解题的关键．
15.【答案】解：| 2−2|−12×(−13)+ 183
=2− 2+4+3 23
=2− 2+4+ 2
=6.
【解析】先化简各式，然后再进行计算即可解答．
本题考查了二次根式的混合运算，实数的运算，准确熟练地进行计算是解题的关键．
16.【答案】解：2x2+5x−12=0，
移项，得2x2+5x=12，
x2+52x=6，
配方，得x2+52x+2516=6+2516，即(x+54)2=12116，
开方，得x+54=±114，
解得：x1=32，x2=−4.
【解析】移项，方程两边都除以2，再配方，开方，即可得出两个方程，再求出方程的解即可．
本题考查了解一元二次方程，能正确配方是解此题的关键．
17.【答案】解：∵四边形ABCD是平行四边形，
∴OB=OD，
∵OE⊥BD，
∴BE=ED，
∴∠CBD=∠BDE=15∘，
∵∠CDE=15∘，
∴∠BDC=30∘，
∵四边形ABCD是平行四边形，
∴AB//CD，
∴∠ABD=∠BDC=30∘，
∴∠ABC=∠ABD+∠CBD=30∘+15∘=45∘.
【解析】由线段垂直平分线的性质得出BE=ED，得出∠CBD=∠BDE=15∘，求出∠ABD=30∘，则可得出答案．
本题考查了平行四边形的性质，平行线的性质，等腰三角形的性质，熟练掌握平行四边形的性质是解题的关键．
18.【答案】解：根据题意得：AC=CD，∠ABD=90∘.
在直角三角形ABD中，
∵AB=3000，AD=5000，
∴BD= AD2−AB2=4000(m)，
设CD=AC=x米，BC=4000−x(米)，
在Rt△ABC中，AC2=AB2+BC2，
即x2=30002+(4000−x)2
解得：x=3125，
答：该超市与车站D的距离是3125米．
【解析】根据题意，AC=CD，∠ABD=90∘，由AB、AD的长易求BD，设CD=x米，则AC=x，BC=BD−x.在直角三角形ABC中运用勾股定理得关系式求解．
本题主要考查了勾股定理的应用，正确得出BD的长是解题关键．
19.【答案】证明：(1)∵四边形ABCD是平行四边形，且对角线AC、BD交于点O，
∴OA=OC，
∵OE=OF，
∴.四边形AECF是平行四边形，
∵OE=OF=OA，
∴OE=OA，OF=OC，
∴OE+OF=OA+OC，
∴AC=EF，
∴四边形AECF是矩形；
(2)∵四边形ABCD是平行四边形，
∴AD//BC，AD=BC，
∴∠DAC=∠BCA，
∵AC平分∠BAD，
∴∠BAC=∠DAC，
∴∠BAC=∠BCA，
∴AB=BC，
∴AB=AD，
∴AO⊥BD，
∵OE=OF，
∴AC是EF的垂直平分线，
∴AE=AF.
【解析】(1)先证明四边形AECF是平行四边形，再证明四边形AECF是矩形即可；
(2)根据平行四边形的性质证明∠DAC=∠BCA，再证明AB=BC，得出AB=AD，进一步证明AC是EF的垂直平分线即可得出结论．
本题主要考查了平行四边形的判定与性质，矩形的判定，等腰三角形的判定，线段垂直平分线的判定与性质，熟练运用相关知识是解答本题的关键．
20.【答案】3 4 4 7 399 4
【解析】解：(1)由所给图形可知，
第①个图形中小正方形的个数为：1=1×3−2，大正方形的个数为：2；
第②个图形中小正方形的个数为：4=2×3−2，大正方形的个数为：3；
第③个图形中小正方形的个数为：7=3×3−2，大正方形的个数为：4；
…，
所以第n个图形中小正方形的个数为(3n−2)个，大正方形的个数为(n+1)个．
故答案为：3，4，4，7.
(2)由(1)发现的结论可知，
当n=100时，
3n−2+n+1=4n−1=4×100−1=399(个)，
即第100个图形中正方形的个数399个．
故答案为：399.
(3)由(1)发现的结论可知，
3n−2=2(n+1)，
解得n=4，
故答案为：4.
(4)不存在．
由(1)可知第n个图形中小正方形的个数为(3n−2)个，大正方形的个数为(n+1)个．
3n−2=(n+1)2，
整理得：n2−n+3=0，
Δ=1−12=−11<0
方程无解．
所以不存在一个图形，这个图形中小正方形的个数是大正方形个数的平方．
(1)依次求出图形中小正方形和大正方形的个数即可解决问题．
(2)根据(1)中发现的规律即可解决问题．
(3)根据(1)中发现的规律即可解决问题．
(4)根据(1)中发现的规律即可解决问题．
本题考查图形变化的规律，能根据所给图形用含n的代数式表示出第n个图形中小正方形和大正方形的个数是解题的关键．
21.【答案】60 3
【解析】解：(1)抽样调查的学生总数为：18÷30%=60(名)；
故答案为：60；
(2)读4本的人数有：60−3−18−21−6=12(人)，
补全条形统计图如下：
(3)把这些数从小到大排列，处于中间位置的是第30、31个数的平均数，
则四月份“读书量”的中位数为3+32=3(本)；
故答案为：3；
(4)1200×660=120(名)，
答：估计该校学生中，四月份“读书量”为5本的学生有120名．
(1)根据2本的人数和所占的百分比求出抽样调查的学生总数；
(2)用总人数减去其它人数求出读4本人数，从而补全条形统计图；
(3)根据中位数的定义即可求出答案；
(4)用总人数乘以样本中四月份“读书量”为5本的学生所占的百分比即可．
本题考查的是条形统计图，众数，用样本估计总体，读懂统计图是解题的关键．
22.【答案】解：(1)设a2+b2=m，则原方程变为m(2m−1)=3，
整理得2m2−m−3=0，
(2m−3)(m+1)=0，
解得m=32或m=−1，
∵a2+b2≥0，
∴a2+b2=32，
∴3a2+3b2−1=3×32−1=72，
(2)设最小正整数为x，由题意得x(x+1)(x+2)(x+3)=24，
整理得(x2+3x)(x2+3x+2)=24，
设x2+3x=y，则方程化为y2+2y−24=0，
(y−4)(y+6)=0，
解得y1=−6，y2=4，
∵x为正整数，
∴y=x2+3x=4，
(x+4)(x−1)=0，
解得x1=1，x2=−4<0(舍去)，
故这四个连续正整数为1，2，3，4.
【解析】(1)设a2+b2=m，则原方程可变为m(2m−1)=3，解方程即可得到a2+b2=32，代入3a2+3b2−1即可求解；
(2)设最小正整数为x，则x(x+1)(x+2)(x+3)=24，整理得到(x2+3x)(x2+3x+2)=24，设x2+3x=y，则y2+2y−24=0，解方程求出y的值，根据x为正整数，得出x2+3x=4，进一步解方程，即可得到结论．
本题主要考查换元法解一元二次方程，换元的实质是转化，关键是构造元和设元.
23.【答案】(1)证明：∵四边形ABCD是矩形，
∴AE//CF，
∴∠EAO=∠FCO，
∵EF垂直平分AC，
∴AO=CO，∠AOE=∠COF=90∘，
在△AOE和△COF中，
∠EAO=∠FCOAO=CO∠AOE=∠COF，
∴△AOE≌△COF(ASA)，
∴OE=OF，
又∵AO=CO，
∴四边形AFCE是平行四边形，
∵EF⊥AC，
∴平行四边形AFCE是菱形；
(2)152
(3)53
【解析】(1)见答案；
(2)如图2，连接CE，AC，
∵AB=6，BC=8，
∴AC= AB2+BC2= 62+82=10，
∵将矩形ABCD沿直线EF翻折，使点C的对称点与点A重合，
∴EF垂直平分AC，
由(1)得：四边形AFCE是菱形，
∴CF=AF=AE，
设CF=AF=AE=x，则BF=8−x，
由勾股定理得：62+(8−x)2=x2，
解得x=254，
∴CF=254，
∴S菱形AFCE=12AC⋅EF=CF⋅AB，
∴12×10⋅EF=254×6，
∴EF=152；
故答案为：152；
(3)如图3，过点A作AN⊥CB，交CB延长线于点N，
∵将平行四边形ABCD沿直线EF翻折，使点C的对称点与点A重合，
则由(1)可知：四边形AFCE是菱形，
∴AF=CF，
∵四边形ABCD是平行四边形，
∴CD//AB，
∴∠BCD=∠ABN=45∘，
∵AB= 2，
∴AN=NB=1，
设AF=CF=x，则BF=2−x，
∴NF=3−x，
在Rt△ANF中，由勾股定理得：
AN2+NF2=AF2，
∴12+(3−x)2=x2，
解得x=53，
∴CF=53，
∴S菱形AFCE=CF⋅AN=53.
故答案为：53.
(1)因为四边形ABCD是矩形，得AE//CF，所以∠EAO=∠FCO，根据EF垂直平分AC，得AO=CO，∠AOE=∠COF，通过ASA即可证明△AOE≌△COF；
(2)连接CE，AC，根据翻折，同理可得四边形AFCE是菱形，设CF=AF=AE=x，则BF=8−x，由勾股定理得：62+(8−x)2=x2，可求出CF的长，再根据S菱形AFCE=12AC⋅EF=CF⋅AB，代入计算即可；
(3)过点A作AN⊥CB，交CB延长线于点N，可求出AN=NB=1，设AF=CF=x，则BF=2−x，则NF=3−x，在Rt△ANF中，由勾股定理得12+(3−x)2=x2，CF=53，即可求出答案；
本题是四边形综合题，考查了平行四边形的性质，菱形的性质，全等三角形的判定与性质等知识点，利用(1)的结论，判断出四边形AFCE是菱形是解题的关键．年龄/岁
18
19
20
21
人数
2
4
3
1
图形编号
①
②
③
…
大正方形/个
2
______
______
…
小正方形/个
1
______
______
…