高中第四节 用单摆测量重力加速度学案

这是一份高中第四节 用单摆测量重力加速度学案，共7页。学案主要包含了实验目的，实验器材，实验原理，注意事项等内容，欢迎下载使用。

一、实验目的
1.练习使用秒表和米尺，测单摆的周期和摆长．
2.用单摆测出当地重力加速度g的值．
二、实验器材
铁架台及铁夹，金属小球(有孔)、秒表、细线(1 m左右)、刻度尺、游标卡尺．
三、实验原理
由T＝2π eq \r(\f(L,g)) ，得g＝ eq \f(4π2L,T2) ，则测出单摆的摆长L和周期T，即可求出当地的重力加速度．
一、实验步骤
1.让细线穿过小球上的小孔，在细线的穿出端打一个稍大一些的线结，制成一个单摆．
2.将铁夹固定在铁架台上端，铁架台放在实验桌边，把单摆上端固定在铁夹上，使摆球自由下垂，在单摆平衡位置处做上标记．
3.用刻度尺量出悬线长L′(准确到mm)，用游标卡尺测出摆球的直径d，则摆长为L＝L′＋ eq \f(d,2) .
4.把单摆拉开一个角度，角度不大于5°，释放摆球．摆球经过最低位置时，用秒表开始计时，测出单摆完成30次(或50次)全振动的时间，求出一次全振动的时间，即为单摆的振动周期．
5.改变摆长，反复测量几次，将数据填入表格．
二、数据处理
(1)公式法：每改变一次摆长，将相应的L和T代入公式g＝ eq \f(4π2L,T2) 中求出g值，最后求出g的平均值．
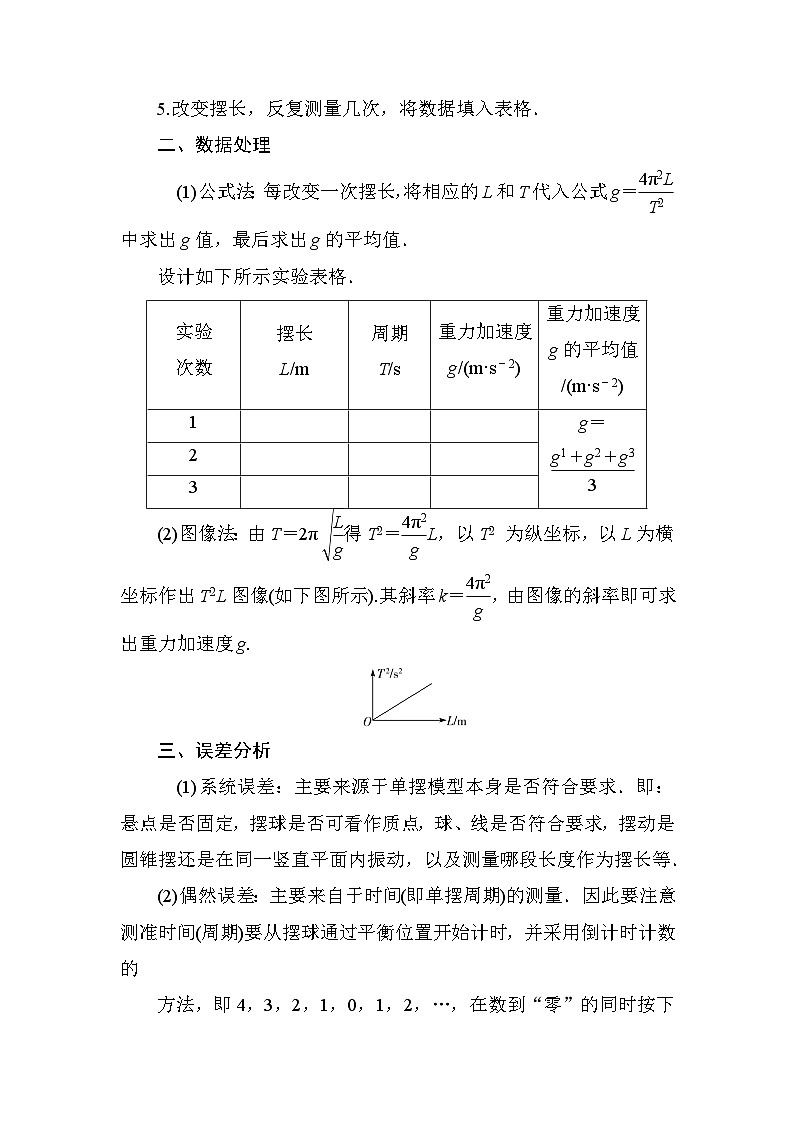
设计如下所示实验表格．
(2)图像法：由T＝2π eq \r(\f(L,g)) 得T2＝ eq \f(4π2,g) L，以T2 为纵坐标，以L为横坐标作出T2L图像(如下图所示).其斜率k＝ eq \f(4π2,g) ，由图像的斜率即可求出重力加速度g.
三、误差分析
(1)系统误差：主要来源于单摆模型本身是否符合要求．即：悬点是否固定，摆球是否可看作质点，球、线是否符合要求，摆动是圆锥摆还是在同一竖直平面内振动，以及测量哪段长度作为摆长等．
(2)偶然误差：主要来自于时间(即单摆周期)的测量．因此要注意测准时间(周期)要从摆球通过平衡位置开始计时，并采用倒计时计数的
方法，即4，3，2，1，0，1，2，…，在数到“零”的同时按下秒表开始计时．不能多计或漏计振动次数．为了减小偶然误差，应进行多次测量后取平均值．
四、注意事项
(1)选择细而不易伸长的线，长度一般不应短于1 m；摆球应选用密度较大、直径较小的金属球．
(2)摆动时控制摆线偏离竖直方向的角度应很小．
(3)摆球摆动时，要使之保持在同一竖直平面内，不要形成圆锥摆．
(4)计算单摆的全振动次数时，应从摆球通过最低位置时开始计时，要测n次全振动的时间t.
类型一 实验原理及操作
【典例1】 根据单摆周期公式T＝2π eq \r(\f(l,g)) ，可以通过实验测量当地的重力加速度．如图甲所示，将细线的上端固定在铁架台上，下端系一小钢球，就做成了单摆．
(1)用游标卡尺测量小钢球直径，示数如图乙所示，读数为________mm.
(2)以下是实验过程中的一些做法，其中正确的有________．
a．摆线要选择细些的、伸缩性小些的，并且尽可能长一些
b．摆球尽量选择质量大些、体积小些的
c．为了使摆的周期大一些，以方便测量，开始时拉开摆球，使摆线相距平衡位置有较大的角度
d．拉开摆球，使摆线偏离平衡位置不大于5°，在释放摆球的同时开始计时，当摆球回到开始位置时停止计时，此时间间隔Δt即为单摆周期T
e．拉开摆球，使摆线偏离平衡位置不大于5°，释放摆球，当摆球振动稳定后，从平衡位置开始计时，记下摆球做50次全振动所用的时间Δt，则单摆周期T＝ eq \f(Δt,50)
答案：(1)18.6 (2)abe
解析：(1)该游标尺为十分度的，根据读数规则可读出小钢球直径为18 mm＋6×0.1 mm＝18.6 mm.
(2)根据用单摆测量重力加速度的实验要求可判断a、b、e正确．
类型二 实验数据处理和误差分析
【典例2】 某同学在做利用单摆测重力加速度的实验中，先测得摆线长为97.50 cm，摆球直径为2.00 cm，然后用秒表记录了单摆振动50次所用的时间为99.7 s，则：
(1)该摆摆长约为________cm，周期约为________s(计算结果保留2位小数).
(2)如果测得g值偏小，可能的原因是________．
A．测摆线长时摆线拉得过紧
B．测量悬线长度作为摆长，没有加上摆球的半径
C．开始计时时，秒表过迟按下
D．实验中误将49次全振动次数记为50次
(3)某同学在“用单摆测定重力加速度”的实验中，测量5种不同摆长情况下单摆的振动周期，记录数据如下：
试以l为横坐标，T2 为纵坐标，如下图所示，作出T2l图线，并利用此图线求出重力加速度为________m/s2( 保留2位小数).
答案：(1)98.50 1.99 (2)B (3)见解析图 9.86
解析：(1)单摆的摆长l＝l′＋ eq \f(d,2) ＝97.50 cm＋1.00 cm＝98.50 cm，周期T＝ eq \f(t,50) ＝ eq \f(99.7 s,50) ≈1.99 s.
(2)由单摆周期公式T＝2π eq \r(\f(l,g)) ，得g＝ eq \f(4π2l,T2) .
测摆线长时摆线拉得过紧，会使l变大，故会使g变大，A错误；测量悬线长度作为摆长，没有加上摆球的半径，l变小，故使g变小，B正确；开始计时时，秒表过迟按下，会使周期T变小，故会使g变大，C错误；实验中误将49次全振动次数记为50次，会使周期T变小，故会使g变大，D错误．
(3)根据表格中的数据选择合适的标度，作出T2l图线如下图所示，
由单摆周期公式T＝2π eq \r(\f(l,g)) ，得T2＝ eq \f(4π2,g) l，
即作出的T2l图线的斜率k＝ eq \f(4π2,g) ，故g＝ eq \f(4π2,k) ，
由上图可知k＝4，所以g＝π2≈9.86 m/s2.
类型三 实验创新应用
【典例3】 某同学利用单摆测定当地重力加速度，实验装置如图甲所示，实验时使摆球在垂直于纸面的平面内摆动，为了将人工记录改为自动记录，在摆球运动最低点的右侧放一激光光源，在其左侧放一个与自动记录仪相连的光敏电阻．他用刻度尺测量细绳的悬点到均匀小球的顶端的距离当作摆长，测得摆长为L1时，仪器显示的光敏电阻R随时间t变化的图线如图乙所示．
(1)从图乙可以看出，摆长为L1时振动周期为________Ｗ．
(2)若保持悬点到小球顶端距离不变，换用直径为原来一半的另一均匀小球进行实验，则图乙中的t1将________(选填“变大”“不变”或“变小”).
(3)通过改变摆线长度，测得6组L和对应的周期T，画出T2L图线如图丙所示，由该直线的斜率可求出重力加速度．与摆线长度加上小球半径作为摆长相比，此法求得的重力加速度________(选填“偏大”“偏小”或“相同”).
答案：(1)2t1 (2)变小 (3)相同
解析：(1)单摆在一个周期内两次经过平衡位置，每次经过平衡位置，单摆会挡住细激光束，从题图乙可以看出，摆长为L1时振动周期为2t1.
(2)根据公式T＝2π eq \r(\f(L,g)) 可知，若保持悬点到小球顶端距离不变，换用直径为原来一半的另一均匀小球进行实验，则题图乙中的t1将变小．
(3)由T＝2π eq \r(\f(L,g)) 整理可得T2＝ eq \f(4π2,g) L，
可知图线斜率k＝ eq \f(4π2,g) ，
若用摆线长度加上小球半径作为摆长有T＝2π eq \r(\f(L＋r,g)) ，
整理可得T2＝ eq \f(4π2,g) L＋ eq \f(4π2r,g) ，
可知图线斜率k′＝ eq \f(4π2,g) ，
可知g与摆长无关，则由该直线的斜率可求出重力加速度，与摆线长度加上小球半径作为摆长相比，此法求得的重力加速度相同．实验
次数
摆长
L/m
周期
T/s
重力加速度
g/(m·s－2)
重力加速度g的平均值/(m·s－2)
1
g＝ eq \f(g1＋g2＋g3,3)
2
3
l/m
0.5
0.8
0.9
1.0
1.2
T2/s2
2.02
3.20
3.61
4.00
4.84