

2023-2024学年河南省周口市西华县八年级(下)期末数学试卷(含答案)
展开1.下列各式一定是二次根式的是( )
A. 6B. −3C. 35D. a
2.下列函数中,y是x的一次函数的是( )
A. y=2B. y=2x+1C. y=2xD. y=x2
3.下列计算正确的是( )
A. (−2)3=−6B. 7− 5= 2
C. 3−27+(− 3)2=0D. |1.73− 3|=1.73− 3
4.在抗击“新型冠状病毒肺炎”疫情中,某社区志愿者小分队年龄如表:
则这10名队员年龄的中位数、众数分别是( )
A. 20岁,35岁B. 22岁,22岁C. 26岁、22岁D. 30岁,30岁
5.已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )
A. ∠A=∠BB. ∠A=∠CC. AC=BDD. AB⊥BC
6.△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列条件中,不能判定△ABC是直角三角形的是( )
A. ∠A:∠B:∠C=3:4:5B. (a+b)(a−b)=c2
C. ∠A+∠B=∠CD. a:b:c=1: 3:2
7.对于一次函数y=2x−3,下列结论错误的是( )
A. 函数的图象与y轴的交点坐标是(0,−3)
B. 函数的图象不经过第二象限
C. 函数值随自变量x值的增大而增大
D. 函数的图象是由函数y=2x的图象向上平移3个单位长度得到的
8.如图,E,F是四边形ABCD两边AB,CD的中点,G,H是两条对角线AC,BD的中点.若EH=3,则以下说法不正确的是( )
A. EH//GF B. GF=3
C. AD=6 D. BC=6
9.如图,矩形ABCD中,直线MN垂直平分AC,与CD,AB分别交于点M,N.若DM=1,CM=2,则矩形的对角线AC的长为( )
A. 2 3
B. 3
C. 5
D. 4
10.如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A. B. C. D.
二、填空题:本题共5小题,每小题3分,共15分。
11.要使 −a有意义,则a的取值范围是______.
12.已知点(2, 3)在一次函数y=kx+b的图象上,则代数式4k+2b的值为______.
13.“五一”期间,某校在各年级开展合唱比赛,规定每支参赛队伍的最终成绩按歌曲内容占30%,演唱技巧占50%,精神面貌占20%考评,某参赛队歌曲内容获得92分,演唱技巧获得94分,精神面貌获得92分,则该参赛队的最终成绩是______分.
14.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示,“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为6,大正方形的面积为23,直角三角形中短直角边长为a,较长直角边长为b,那么(a+b)2的值为______.
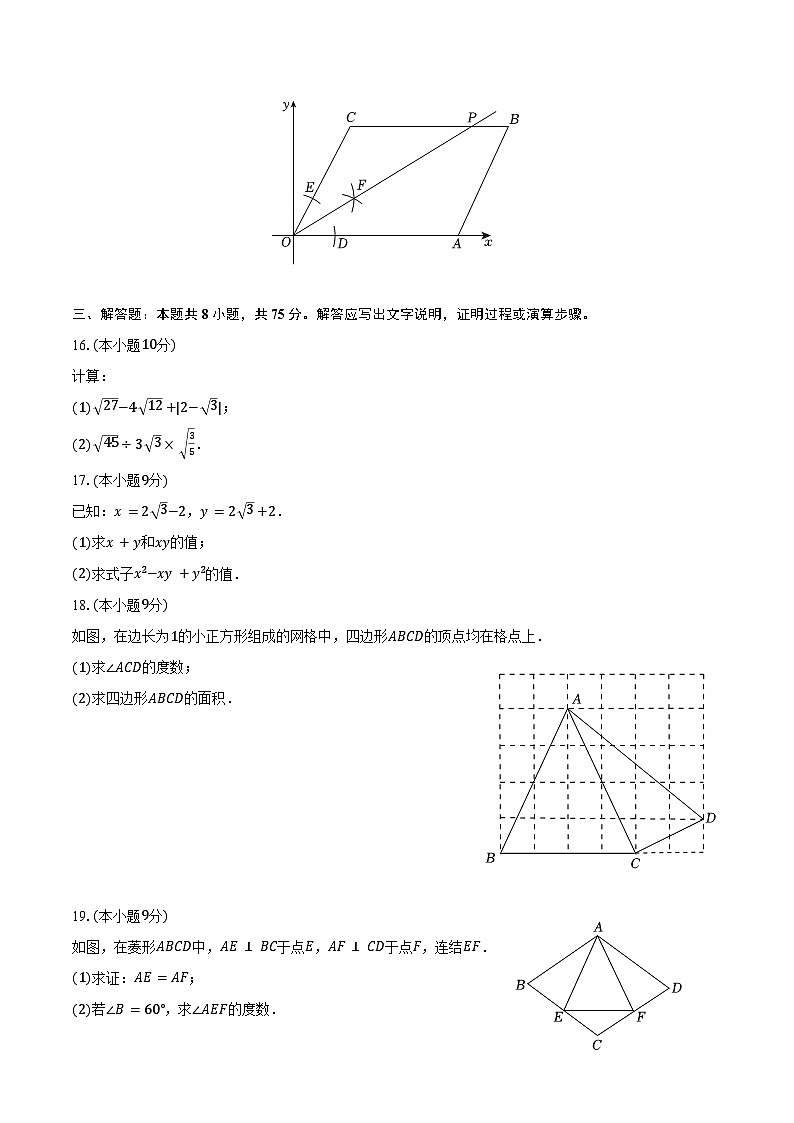
15.如图,在平面直角坐标系中,▱OABC的顶点A在x轴上,OC=6,∠AOC=60°,以点O为圆心,适当长为半径画弧,分别交OA,OC于点D,E;再分别以点D、点E为圆心,大于12DE的长为半径画弧,两弧在∠AOC的内部相交于点F,过点O作射线OF,交BC于点P,则点P的坐标为______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题10分)
计算:
(1) 27−4 12+|2− 3|;
(2) 45÷3 3× 35.
17.(本小题9分)
已知:x=2 3−2,y=2 3+2.
(1)求x+y和xy的值;
(2)求式子x2−xy+y2的值.
18.(本小题9分)
如图,在边长为1的小正方形组成的网格中,四边形ABCD的顶点均在格点上.
(1)求∠ACD的度数;
(2)求四边形ABCD的面积.
19.(本小题9分)
如图,在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,连结EF.
(1)求证:AE=AF;
(2)若∠B=60°,求∠AEF的度数.
20.(本小题9分)
蓬勃发展的快递业,为全国各地的新鲜水果及时走进千家万户提供了极大便利.不同的快递公司在配送、服务、收费和投递范围等方面各具优势.樱桃种植户小丽经过初步了解,打算从甲、乙两家快递公司中选择一家合作,为此,小丽收集了10家樱桃种植户对两家公司的相关评价,并整理、描述、分析如下:
a.配送速度得分(满分,10分);
甲:6 6 7 7 7 8 9 9 9 10
乙:6 7 7 8 8 8 8 9 9 10
b.服务质量得分统计图(满分10分):
c.配送速度和服务质量得分统计表:
根据以上信息,回答下列问题:
(1)表格中的m= ______;s甲2 ______s乙2(填“>”“=”或“<”).
(2)综合上表中的统计量,你认为小丽应选择哪家公司?请说明理由.
(3)为了从甲、乙两家公司中选出更合适的公司,你认为还应收集什么信息(列出一条即可)?
21.(本小题9分)
近年来,市民交通安全意识逐步增强,骑行用头盔需求量增大.某生产厂家销售的甲种头盔单价是70元,乙种头盔单价是56元.某商店欲购进甲、乙两种头盔共100顶,正好赶上厂家进行促销活动,促销方式如下:甲种头盔按单价的八折出售,乙种头盔每顶降价6元出售.如果此次购买甲种头盔的数量不低于乙种头盔的数量,那么应购买多少顶甲种头盔能使此次购买头盔的总费用最少?最少费用是多少元?
22.(本小题10分)
如图,在平行四边形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形ADFE是矩形;
(2)连接OF,若AD=6,EC=4,∠ABF=60°,求OF的长度.
23.(本小题10分)
如图,在平面直角坐标系中,直线l1:y=−12x+6分别与x轴、y轴交于点B,C,与直线l2:y=12x交于点A.
(1)求点A的坐标;
(2)若D是线段OA上的点,且D点的横坐标为4,求出直线CD的函数解析式.
(3)在第(2)小题的条件下,射线CD上是否存在点P,使以O,C,P为顶点的三角形是等腰直角三角形?若存在,请写出点P的坐标;若不存在,请说明理由.
参考答案
1.A
2.B
3.C
4.C
5.B
6.A
7.D
8.D
9.A
10.B
11.a≤0
12.2 3
13.93
14.40
15.(9,3 5)
16.解:(1) 27−4 12+|2− 3|
=3 3−8 3+2− 3
=2−6 3;
(2) 45÷3 3× 35
=13 453× 35
=13 453×35
=13 9
=13×3
=1.
17.解:(1)x+y=2 3−2+2 3+2=4 3;
xy=(2 3−2)(2 3+2)=(2 3)2−22=12−4=8.
(2)∵x+y=4 3,xy=8,
∴x2−xy+y2
=(x+y)2−3xy
=(4 3)2−3×8
=48−24
=24.
18.解:(1)根据题意得:AC= 42+22=2 5,CD= 22+12= 5,AD= 32+42=5.
∵AC2+CD2=(2 5)2+( 5)2=25=52=AD2.
∴∠ACD=90°;
(2)S四边形ABCD=S△ABC+S△ACD=12×4×4+12× 5×2 5=8+5=13.
19.(1)证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D.
又∵AE⊥BC于点E,AF⊥CD于点F,
∴∠AEB=∠AFD=90°,
在△ABE与△ADF中,
∵∠B=∠D∠AEB=∠AFDAB=AD.
∴△ABE≌△ADF(AAS).
∴AE=AF;
(2)解:∵四边形ABCD是菱形,
∴∠B+∠BAD=180°.
而∠B=60°,
∴∠BAD=120°.
又∵∠AEB=90°,∠B=60°,
∴∠BAE=30°.
由(1)知△ABE≌△ADF,
∴∠BAE=∠DAF=30°.
∴∠EAF=120°−30°−30°=60°.
∴△AEF是等边三角形.
∴∠AEF=60°.
20.(1)7.5,<;
(2)小丽应选择甲公司(答案不唯一),理由如下:
∵配送速度得分甲和乙的得分相差不大,服务质量得分甲和乙的平均数相同,但是甲的方差明显小于乙的方差,
∴甲更稳定,
∴小丽应选择甲公司;
(3)还应收集甲、乙两家公司的收费情况.(答案不唯一,言之有理即可)
21.解:设购m只甲种头盔,则购(100−m)只乙种头盔,设总费用为w元,
则m≥100−m,
解得:m≥50,
w=0.8×70m+(56−6)(100−m)=6m+5000,
∵6>0,
∴w随m的增大而增大,
∴m=50时,w取最小值,最小值=6×50+4800=7800,
答:应购买50个甲种头盔可以使此次购买头盔的总费用最少,最少费用是7800元.
22.(1)证明:∵四边形ABCD是平行四边形,
∴AB//DC且AB=DC,
∴∠ABE=∠DCF,
在△ABE和△DCF中,AB=DC∠ABE=∠DCFBE=CF,
∴△ABE≌△DCF(SAS),
∴AE=DF,∠AEB=∠DFC,
∴AE//DF,
∴四边形ADFE是平行四边形
∵AE⊥BC
∴∠AEF=90°,
∴四边形ADFE是矩形;
(2)解:由(1)知:四边形ADFE是矩形,
∴EF=AD=6,
∵EC=4,
∴BE=CF=2,
∴BF=8,
Rt△ABE中,∠ABE=60°,
∴AB=2BE=4,
∴DF=AE= AB2−BE2=2 3,
∴BD= BF2+DF2= 82+(2 3)2=2 19,
∵四边形ABCD是平行四边形,
∴OB=OD,O是Rt△BDF斜边上的中点
∴OF=12BD= 19.
23.解:(1)联立直线l1、l2的表达式得:−12x+6=12x,
解得:x=6,
∴A(6,3);
(2)∵直线l1:y=−12x+6分别与x轴、y轴交于点B、C,
则点B、C的坐标分别为(12,0)、(0,6),
当x=4时,y=12x=2,
∴D(4,2),
由点C、D的坐标得,直线CD解析式为y=−x+6;
(3)存在点P,使以O、C、P、Q为顶点的四边形是菱形,
如图所示,分三种情况考虑:
(i)当四边形OP1Q1C为菱形时,由∠COP1=90°,得到四边形OP1Q1C为正方形,此时OP1=OC=6,即P1(6,0);
(ii)当四边形OP2CQ2为菱形时,由C坐标为(0,6),得到P2纵坐标为3,
把y=3代入直线CP1的解析式y=−x+6中,可得3=−x+6,解得x=3,此时P2(3,3);
(iii)当四边形OQ3P3C为菱形时,则有OQ3=OC=CP3=P3Q3=6,设P3(x,−x+6),
∴x2+(−x+6−6)2=62,解得x=±3 2(舍去负值),此时P3(3 2,−3 2+6);
综上可知存在满足条件的点的P,其坐标为(6,0)或(3,3)或(3 2,−3 2+6). 年龄(岁)
18
22
30
35
43
人数
2
3
2
2
1
项目
统计量
快递公司
配送速度得分
服务质量得分
平均数
中位数
平均数
方差
甲
7.8
m
7
s甲2
乙
8
8
7
s乙2
河南省周口市西华县2023-2024学年七年级上学期期末数学试卷+: 这是一份河南省周口市西华县2023-2024学年七年级上学期期末数学试卷+,共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年河南省周口市西华县七年级(上)期末数学试卷(含解析): 这是一份2023-2024学年河南省周口市西华县七年级(上)期末数学试卷(含解析),共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年河南省周口市西华县八年级(上)期中数学试卷(含解析): 这是一份2023-2024学年河南省周口市西华县八年级(上)期中数学试卷(含解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












