华东师大版初中八年级数学上册第12章整式的乘除素养综合检测课件

这是一份华东师大版初中八年级数学上册第12章整式的乘除素养综合检测课件，共28页。

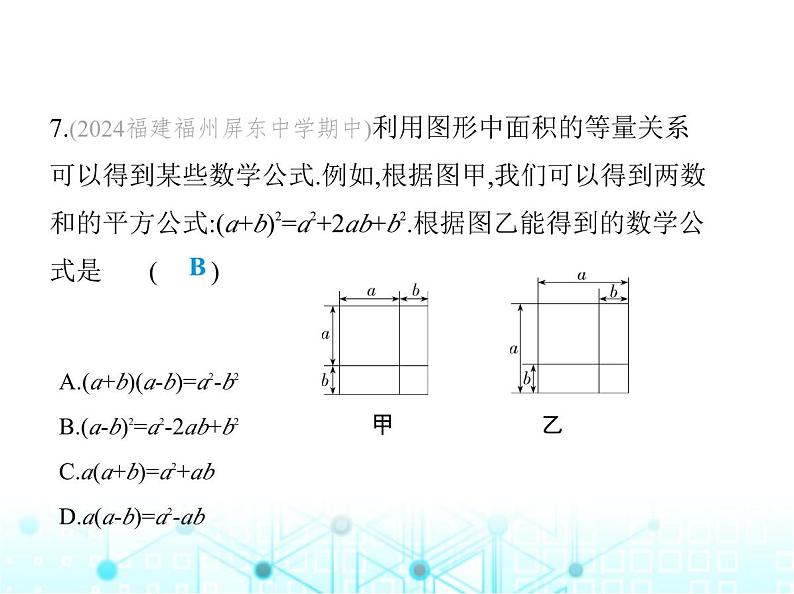
第12章　素养综合检测(满分100分, 限时60分钟)一、选择题(每小题3分,共30分)1.(2023湖南长沙中考)下列计算正确的是 (　    )A.x2·x3=x5　　　    B.(x3)3=x6C.x(x+1)=x2+1　　　    D.(2a-1)2=4a2-1A解析    x2·x3=x5,故选项A符合题意;(x3)3=x9≠x6,故选项B不符合题意;x(x+1)=x2+x≠x2+1,故选项C不符合题意;(2a-1)2=4a2-4a+1≠4a2-1,故选项D不符合题意.故选A.2.(2024河南周口淮阳月考)若a·am·a3m+1=a14,则m的值为(       )A.1　　　    B.2　　　    C.3　　　    D.4C 解析　∵a·am·a3m+1=a1+m+3m+1=a4m+2=a14,∴4m+2=14.∴m=3.故选C.3.(2023四川巴中巴州月考)下列多项式中可以用公式法因式分解的是 (　    )A.m2+n2　　　    B.-a2-b2C.x2+x+1　　　    D.x2-x+  D解析    A、B、C均不能用公式法因式分解,故不符合题意;x2-x+ = ,故D符合题意.故选D.4.(类比思想)(2024海南华侨中学期中)若(x-3y)(x+2y)=x2+mxy+ny2,则m,n的值分别是 (　    )A.-1,6　　　    B.1,6　　　    C.-1,-6　　　    D.1,-6C 解析　∵(x-3y)(x+2y)=x2+2xy-3xy-6y2=x2-xy-6y2=x2+mxy+ny2,∴m=-1,n=-6.故选C.5.运用乘法公式计算(a+2b-2)2,得到的结果是 (　    )A.a2+4b2+4ab-4a-4b+4B.a2+4b2+2ab-2a-4b+4C.a2+4b2+4ab-4a-8b+4D.a2+4b2+4ab-4a+8b+4C 解析　原式=[(a+2b)-2]2=(a+2b)2-4(a+2b)+4=a2+4ab+4b2-4a-8b+4,故选C.6.已知x-y=-1,xy=4,则(x+y)2的值为 (　    )A.1　　　    B.7　　　    C.15　　　    D.17D解析　∵x-y=-1,xy=4,∴(x+y)2=(x-y)2+4xy=(-1)2+4×4=1+16=17.故选D.7.(2024福建福州屏东中学期中)利用图形中面积的等量关系可以得到某些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.根据图乙能得到的数学公式是     (　    )A.(a+b)(a-b)=a2-b2B.(a-b)2=a2-2ab+b2C.a(a+b)=a2+abD.a(a-b)=a2-ab甲 乙B解析　题图乙中能得到的数学公式是(a-b)2=a2-2ab+b2.故选B.8.(2023山东聊城实验中学期中)小轩计算一道整式乘法的题:(3x+2m)(5x-6),由于小轩将第一个多项式中的“+2m”抄成“-2m”,得到的结果为15x2-78x+72,则m的值为 (　    )A.4　　　    B.5　　　    C.6　　　    D.7C解析    (3x-2m)(5x-6)=15x2-18x-10mx+12m=15x2-(18+10m)x+12m,∴15x2-(18+10m)x+12m=15x2-78x+72,∴12m=72,18+10m=78,∴m=6.故选C.9.(方程思想)(2023四川巴中巴州期末)若关于x的多项式(x2+ax+2)(2x-4)的展开式中不含x2项,则a的值是 (　    )A.2　　　    B. 　　　    C.0　　　    D.-2A解析    (x2+ax+2)(2x-4)=2x3-4x2+2ax2-4ax+4x-8=2x3+(-4+2a)x2+(-4a+4)x-8,∵(x2+ax+2)(2x-4)的展开式中不含x2项,∴-4+2a=0,解得a=2.故选A.10.(新考向·规律探究试题)(2023四川巴中中考)我国南宋时期数学家杨辉于1261年写下《详解九章算法》,书中记载的图表给出了(a+b)n展开式的系数规律. 当代数式x4-12x3+54x2-108x+81的值为1时,x的值为 (　    )A.2　　　    B.-4　　　    C.2或4　　　    D.2或-4C 解析　依据题中规律可得(a+b)4=a4+4a3b+6a2b2+4ab3+b4,∴x4-12x3+54x2-108x+81=x4+4x3·(-3)+6x2·(-3)2+4x·(-3)3+(-3)4=(x-3)4,∴(x-3)4=1,∴x-3=±1,解得x=2或x=4.故选C.二、填空题(每小题4分,共24分)11.(2024河南南阳西峡期中)计算(直接写出答案):(1)(-2x2)3+4x3·x3=　　　    ;(2)(-6a3b5c)÷(-2ab2)2=　　　    .-4x6解析    (1)(-2x2)3+4x3·x3=-8x6+4x6=-4x6.(2)(-6a3b5c)÷(-2ab2)2=(-6a3b5c)÷(4a2b4)=- abc.12.(分组分解法)(2023黑龙江绥化中考)因式分解:x2+xy-xz-yz=　　　    .(x+y)(x-z)解析　原式=(x2+xy)-z(x+y)=x(x+y)-z(x+y)=(x+y)(x-z).13.(2022四川攀枝花月考)小丽在计算一个二项式的平方时,得到正确结果m2-10mn+■,但最后一项不慎被墨水污染,这一项应是　　　    .25n2 解析　∵m2-10mn+■=m2-2·m·5n+■,∴■=(5n)2=25n2.14.(整体思想)(2023山东济宁中考)已知实数m满足m2-m-1=0,则2m3-3m2-m+9=　　　    .8解析　∵m2-m-1=0,∴m2-m=1.∴2m3-3m2-m+9=(2m3-2m2)-m2-m+9=2m(m2-m)-m2-m+9=2m-m2-m+9=-m2+m+9=-(m2-m)+9=-1+9=8.15.(新考向·新定义试题)(2023四川资阳安岳李家中学期中)现规定一种新运算:a☉b=ab-a2,其中a、b为实数,则(x+y)☉(x-y)等于　　　    .-2y2-2xy解析　由题意得(x+y)☉(x-y)=(x+y)(x-y)-(x+y)2=x2-y2-(x2+2xy+y2)=x2-y2-x2-2xy-y2=-2y2-2xy.16.(新考向·规律探究试题)计算:1002-992+982-972+…+42-32+22-12的值为　　　    . 5 050解析    1002-992+982-972+…+42-32+22-12=(100-99)×(100+99)+(98-97)×(98+97)+…+(4-3)×(4+3)+(2-1)×(2+1)=100+99+98+97+…+4+3+2+1=5 050.三、解答题(共46分)17.(2023福建厦门湖里中学期中)(9分)计算:(1)(2x-5)(3x+2).(2)-(a2b)3+2a2b·(-3a2b)2.(3)(2x+3y)2-(2x+y)(2x-y).解析    (1)原式=6x2+4x-15x-10=6x2-11x-10.(2)原式=-a6b3+2a2b·9a4b2=-a6b3+18a6b3=17a6b3.(3)原式=4x2+12xy+9y2-(4x2-y2)=4x2+12xy+9y2-4x2+y2=12xy+10y2.18.(2024四川资阳安岳期中)(9分)因式分解:(1)12xy2-3x3.(2)(x-1)(x-3)+1.(3)x2(y2-1)+2x(y2-1)+(y2-1).解析    (1)12xy2-3x3=3x(4y2-x2)=3x(2y+x)·(2y-x).(2)(x-1)(x-3)+1=x2-x-3x+3+1=x2-4x+4=(x-2)2.(3)x2(y2-1)+2x(y2-1)+(y2-1)=(x2+2x+1)(y2-1)=(x+1)2(y+1)(y-1).19.(新独家原创)(8分)先化简,再求值:[(x+2y)·(x-2y)-(2x-y)2-(x2-5y2)]÷(-2x),其中x、y满足x2+y2-6x-2y+10=0.解析    [(x+2y)(x-2y)-(2x-y)2-(x2-5y2)]÷(-2x)=(x2-4y2-4x2+4xy-y2-x2+5y2)÷(-2x)=(-4x2+4xy)÷(-2x)=2x-2y.∵x2+y2-6x-2y+10=0,∴x2-6x+9+y2-2y+1=0,∴(x-3)2+(y-1)2=0,∴x-3=0,y-1=0,解得x=3,y=1.∴原式=2×3-2×1=6-2=4.20.(数形结合思想)(2024福建泉州七中期中)(9分)两个边长分别为a和b的正方形如图1放置,其未叠合部分(阴影部分)的面积为S1;若再往图1中大正方形的右下角摆放一个边长为b的小正方形,如图2,两个小正方形叠合部分(阴影部分)的面积为S2.(1)用含a,b的代数式分别表示S1、S2.(2)若a+b=10,ab=20,求S1+S2的值. 图1图2解析    (1)由题意可得S1=a2-b2,S2=a2-a(a-b)-b(a-b)-b(a-b)=a2-a2+ab-ab+b2-ab+b2=2b2-ab.(2)由(1)得,S1+S2=a2-b2+2b2-ab=a2+b2-ab=(a+b)2-3ab,∵a+b=10,ab=20,∴S1+S2=102-3×20=40.21.(跨学科·生物)(11分)某公司培养绿藻以制作绿藻粉,再经过后续的加工步骤,制成绿藻相关的保健食品.已知该公司制作每1克的绿藻粉需要60亿个绿藻细胞.请根据上述信息回答下列问题:(1)假设在光照充沛的环境下,1个绿藻细胞每20小时可分裂成4个绿藻细胞,且分裂后的细胞亦可继续分裂.现从1个绿藻细胞开始培养,若培养期间绿藻细胞皆未死亡且培养环境的光照充沛,经过15天后,共分裂成4k个绿藻细胞,则k的值是多少?(2)在(1)的条件下,已知60亿介于232与233之间,请判断4k个绿藻细胞是否足够制作8克的绿藻粉.解析    (1)15天=15×24小时=360小时,∵1个绿藻细胞每20小时可分裂成4个绿藻细胞,∴从1个绿藻细胞开始培养,经过20小时分裂成4个绿藻细胞,经过20×2=40(小时),分裂成42个绿藻细胞,经过20×3=60(小时),分裂成43个绿藻细胞,……经过20×18=360(小时),分裂成418个绿藻细胞,∴k的值为18.(2)∵每1克的绿藻粉需要60亿个绿藻细胞,∴制作8克的绿藻粉需要60×8亿个绿藻细胞,∵60亿介于232与233之间,∴232×8<60×8亿<233×8,即235<60×8亿<236,∵418=(22)18=236,∴60×8亿<418,∴418个绿藻细胞足够制作8克的绿藻粉.