沪科版九年级上册21.4 二次函数的应用教课ppt课件

这是一份沪科版九年级上册21.4 二次函数的应用教课ppt课件，共25页。

1.(跨学科·体育与健康)(2024安徽芜湖月考)如图,一位篮球运动员正在投篮,球沿抛物线y=ax2+x+2.25行进,然后落入篮筐内,已知篮筐的中心离地面的高度为3.05 m,运动员距篮筐中心的水平距离OH是4 m,则a的值为(M9121004)(　    )A.-0.25　　　B.-0.24　　　C.-0.22　　　    
解析　根据题意得,点(4,3.05)在抛物线y=ax2+x+2.25上,代入 得3.05=16a+4+2.25,解得a=-0.2,故选D.
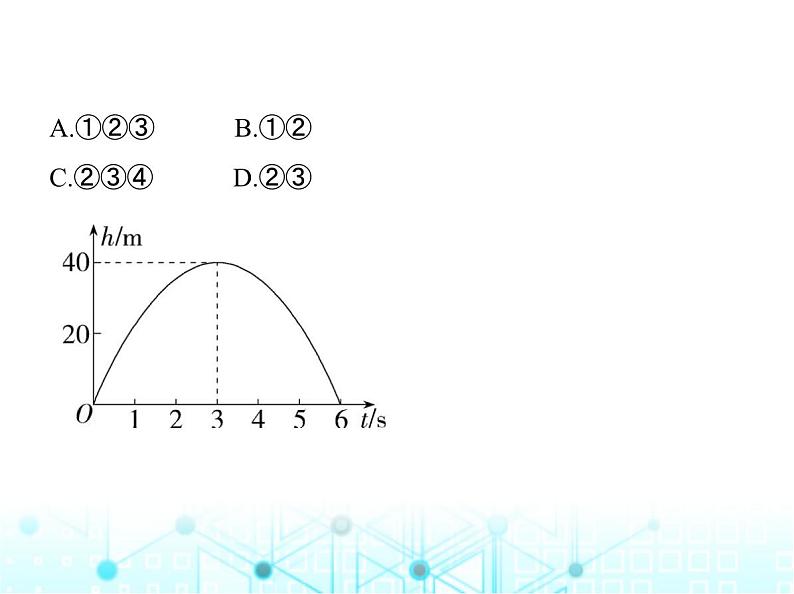
2.(跨学科·物理)(2023安徽六安期中)物理课上我们学习了竖 直上抛运动,若从地面竖直向上抛一小球,小球的高度h(单位: m)与小球运动时间t(单位:s)之间的函数关系如图所示,下列 结论:①小球在空中经过的路程是40 m;②小球抛出3 s后,速度越来越快;③小球抛出3 s时速度为0 m/s;④当h=30时,t=1.5.其中正确的是 (　    )
A.①②③　　　B.①②　　　　　    C.②③④　　　D.②③      
解析　①由图象知小球在空中达到的最大高度是40 m,故小 球在空中经过的路程为40×2=80(m),故①错误;②小球抛出3秒后,速度越来越快,故②正确;③小球抛出3秒时达到最高点即速度为0 m/s,故③正确;④设函数解析式为h=a(t-3)2+40(a≠0),把O(0,0)代入得0=a(0-3)2+40,解得a=- ,∴函数解析式为h=- (t-3)2+40,把h=30代入解析式得30=- (t-3)2+40,
解得t=4.5或t=1.5,∴当h=30时,t=1.5或4.5,故④错误.
3.(教材变式·P38T1)如图,一条单向隧道的截面由抛物线和长 方形构成,长方形的长为8 m,宽为2 m,隧道的最高点P的坐标 为(4,6),如果一辆货车高4 m,宽3 m,那么这辆货车　　　     (填“能”或“不能”)通过该隧道.
4.(2024安徽淮北二中月考)在平面直角坐标系中,某水利工 程公司修建的水渠的横截面如图所示,横截面呈抛物线形,其 宽度AB=30米.某日,水渠内的水面宽度CD为24米,此时水面 到两岸所在平面的距离为1.8米.(M9121004)(1)求该抛物线对应的函数表达式.(2)若水渠中原水面的宽度CD减少到原来的一半,则水渠最 深处到水面的距离减少多少米?
解析    (1)根据题图,设该抛物线对应的函数表达式为y=ax2+ k,由题图得B(15,0),D(12,-1.8),代入表达式得 解得 ∴该抛物线对应的函数表达式为y= x2-5.(2)由(1)得E点坐标为(0,-5),根据题意得当水渠内的水面宽度CD为24米时,水渠最深处 到水面的距离为5-1.8=3.2(米),当水渠中原水面的宽度CD减少到原来的一半时,令x=6,则y=
  ×62-5=-4.2,此时水渠最深处到水面的距离为5-4.2=0.8(米),∴水渠最深处到水面的距离减少3.2-0.8=2.4(米).
5.(2023山东滨州中考,15,  )某广场要建一个圆形喷水池,计划在水池中心位置竖直安装一根顶部带有喷水头的水管, 使喷出的抛物线形水柱在与池中心的水平距离为1 m处达到 最高,高度为3 m,水柱落地处离池中心的水平距离也为3 m, 那么水管的设计高度应为　　　　    .(M9121004)
解析　根据题意建立平面直角坐标系,如图.由题意可知点(1, 3)是抛物线的顶点,∴设这段抛物线的表达式为y=a(x-1)2+3. ∵该抛物线过点(3,0),∴0=a(3-1)2+3,解得a=- .∴y=- (x-1)2+3.∵当x=0时,y=- ×(0-1)2+3=- +3= ,∴水管的设计高度应为  m.
6.(情境题·现实生活)(2024安徽安庆宿松期中,20,  )如图,一座拱桥的轮廓呈抛物线形,拱高6 m,在高度为10 m的两支柱AC和BD之间,还安装了三根支柱,相邻两支柱间的距离均为5 m.(M9121004)(1)建立如图所示的平面直角坐标系,求抛物线的表达式.(2)求支柱EF的长.(3)拱桥下方是地面平坦的双向行车道(正中间是一条宽2 m 的隔离带),其中的一条行车道能否并排行驶三辆宽2 m、高 3.2 m的汽车(汽车间隔忽略不计)?请说说你的理由.
解析    (1)根据题图可知,图象过原点,∴设抛物线的表达式 为y=ax2+bx,∵相邻两支柱间的距离均为5 m,∴AB=4×5=20(m),∴(20,0),(10,6)两点都在抛物线上,代入,得 ∴ ∴y=- x2+ x.(2)当x=15时,y=- ×152+ ×15= ,
∴F .∴EF=10- = =5.5(m).(3)中间隔离带的宽为两米,即隔离带到A或B的距离为9米.因 为三辆汽车并排宽共6米,所以只需比较当x=3时,y的值与3.2 的大小,即可判断.当x=3时,y=- ×32+ ×3=3.06<3.2,∴不能并排行驶三辆宽2 m、高3.2 m的汽车.
7.(项目式学习试题)(2022浙江温州中考)根据以下素材,探索 完成任务.
解析    (答案不唯一)任务1:以拱顶为原点,建立如图所示的直角坐标系,则顶点O的坐标 为(0,0),且图象经过点B(10,-5), 设抛物线的解析式为y=ax2(a≠0),把点B(10,-5)代入得100a=-
5,∴a=- ,∴抛物线的函数表达式为y=- x2.任务2:∵该河段水位再涨1.8 m达到最高,灯笼底部距离水面不小于 1 m,灯笼长0.4 m,∴悬挂点的纵坐标y≥-5+1.8+1+0.4=-1.8,∴悬挂点的纵坐标 的最小值是-1.8.当y=-1.8时,- x2=-1.8,∴x=±6,∴悬挂点的横坐标的取值范围是-6≤x≤6.
任务3:方案一:如图(坐标系的横轴),从原点处开始悬挂灯笼, 当原点一侧悬挂4盏灯笼时,1.6×4=6.4>6;当原点一侧悬挂3 盏灯笼时,1.6×3=4.8<6,∴原点一侧最多悬挂3盏灯笼,∵灯笼挂满后成轴对称分布,∴共可挂7盏灯笼,∴最左边一盏灯笼悬挂点的横坐标为-1.6×3=-4.8.