初中数学冀教版七年级上册2.7 角的和与差课前预习课件ppt

这是一份初中数学冀教版七年级上册2.7 角的和与差课前预习课件ppt，共24页。PPT课件主要包含了学习目标，课堂导入，几何语言，所以∠1与∠2互余，因为∠1与∠2互余，同角的余角相等，等角的余角相等，所以∠1与∠2互补，因为∠1与∠2互补，同角的补角相等等内容，欢迎下载使用。

1.了解两角互余和两角互补的定义.2.通过探究了解“同角(或等角)的余角相等”“同角(或等角)的补角相等”并能利用这些性质进行角的计算，发展推理能力.
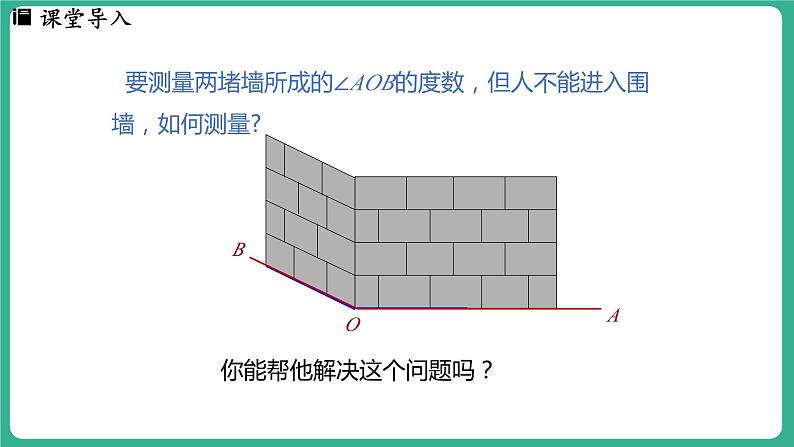
要测量两堵墙所成的∠AOB的度数，但人不能进入围墙，如何测量?
你能帮他解决这个问题吗？
两个角的和等于90°（直角），就说这两个角互为余角，简称互余.
如果∠1+∠2=90°，那么∠1与∠2互为余角.
因为∠1＋∠2＝90°,
反过来，如果∠1与∠2互为余角，那么∠1+∠2=90°.
所以∠1＋∠2＝90°.
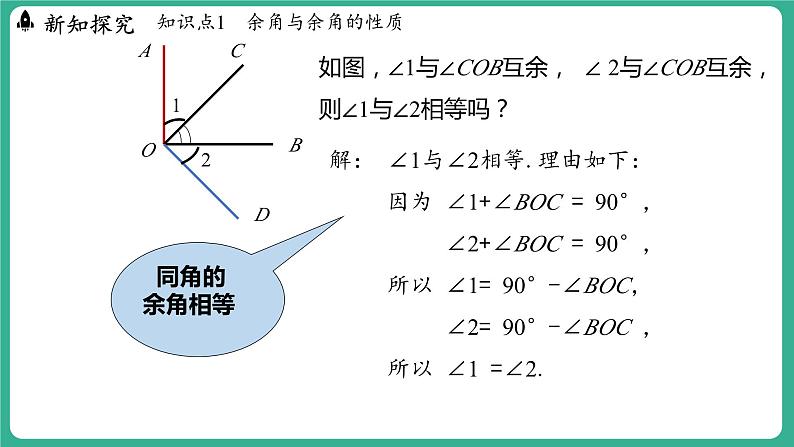
知识点1 余角与余角的性质
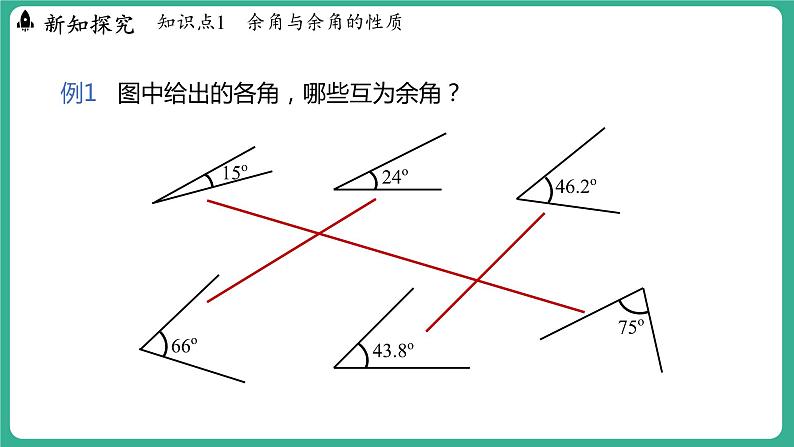
例1 图中给出的各角，哪些互为余角？
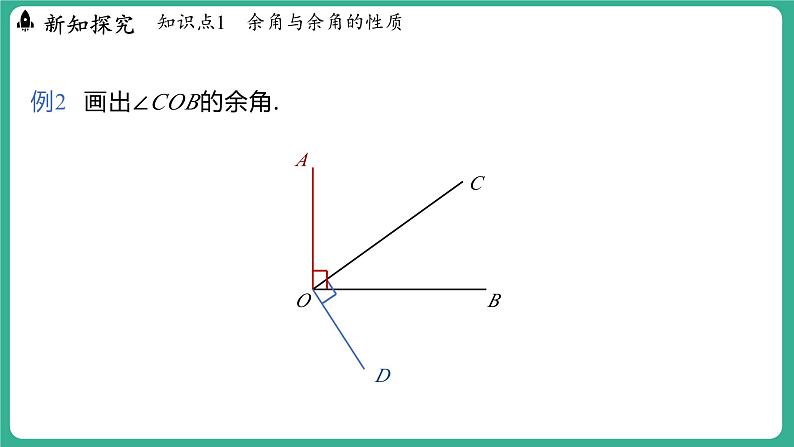
例2 画出∠COB的余角.
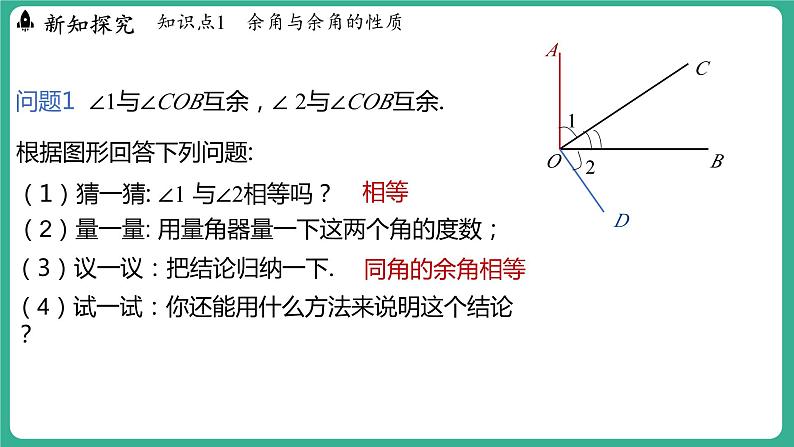
（2）量一量: 用量角器量一下这两个角的度数；
根据图形回答下列问题:（1）猜一猜: ∠1 与∠2相等吗？
问题1 ∠1与∠COB互余，∠ 2与∠COB互余.
（3）议一议：把结论归纳一下.
（4）试一试：你还能用什么方法来说明这个结论？
解： ∠1与∠2相等.理由如下： 因为 ∠1+∠BOC = 90°， ∠2+∠BOC = 90°， 所以 ∠1= 90°-∠BOC， ∠2= 90°-∠BOC ， 所以 ∠1 =∠2.
如图，∠1与∠COB互余， ∠ 2与∠COB互余，则∠1与∠2相等吗？
问题2 如图，∠1与∠2互余，∠3与∠4互余，如果∠1=∠3，那么∠2与∠4相等吗？为什么？
解： ∠2与∠4相等.理由如下： 因为∠1﹢∠2 = 90°， ∠3﹢∠4 = 90°， 所以∠2 = 90°-∠1，∠4 = 90°-∠3. 因为∠1 =∠3, 所以∠2 =∠4.
两个角的和等于180°（平角），就说这两个角互为补角，简称互补.
如果∠1+∠2=180°，那么∠1与∠2互为补角.
因为∠1＋∠2＝180°，
知识点2 补角与补角的性质
反过来，如果∠1与∠2互为补角，那么∠1+∠2=180°.
所以∠1＋∠2＝180°.
例3 图中给出的各角，哪些互为补角？
问题3 如图，∠1是∠BOC 的补角， ∠2是∠BOC 的补角.∠1与∠2相等吗?
解： ∠1与∠2相等.理由如下： 因为∠1+ ∠BOC = 180°， ∠2+ ∠BOC = 180°， 所以∠1=180°- ∠BOC ， ∠2=180°- ∠BOC， 所以∠1=∠2.
问题4 如图，∠1与∠2互补，∠3与∠4互补，如果∠1=∠3，那么∠2与∠4相等吗？为什么？
解：∠2与∠4相等.理由如下： 因为 ∠1﹢∠2 = 180°，∠3﹢∠4 = 180°， 所以 ∠2 = 180°-∠1， ∠4 = 180°-∠3. 因为 ∠1 =∠3， 所以 ∠2 =∠4.
例4 如图，点A，O，B在同一直线上，射线 OD 和射线 OE 分别平分∠AOC 和∠BOC，图中哪些角互为余角？
解：因为点A，O，B在同一直线上， 所以 ∠AOC 和∠BOC互为补角.
所以∠COD和∠COE互为余角.
同理∠AOD和∠BOE，∠AOD和∠COE，∠COD和∠BOE也互为余角.
例5 如图，直线AB与∠COD的两边OC，OD分别相交于点E，F，∠1＋∠2＝180°.找出图中与∠2相等的角，并说明理由．分析：已知∠1＋∠2＝180°，说明∠2是∠1的补角．根据同角(或等角)的补角相等，找出图中∠1的其他补角和∠2的其他补角的补角，便可确定与∠2相等的角．
解：如图，因为∠1＋∠3＝180°，∠1＋∠2＝180°， 所以∠3＝∠2. 因为∠1＋∠4＝180°，∠1＋∠2＝180°， 所以∠4＝∠2. 因为∠2＋∠5＝180°， ∠6＋∠5＝180°， 所以∠2＝∠6. 所以图中与∠2相等的角有∠3，∠4，∠6.
例5 如图，直线AB与∠COD的两边OC，OD分别相交于点E，F，∠1＋∠2＝180°.找出图中与∠2相等的角，并说明理由．
1.一个角的余角是它的2倍，这个角的度数是（　）A．30°B．45°C．60°D．75°
2.下列说法正确的是（　　）A．一个角的补角一定大于它本身B．一个角的余角一定小于它本身C．一个钝角减去一个锐角的差一定是一个锐角D．一个角的余角一定小于其补角
3. 如图，直线AB，CD交于点O，因为∠1＋∠3＝180°，∠2＋∠3＝180°，所以∠1＝∠2的依据是(　　)A．同角的余角相等 B．等角的余角相等C．同角的补角相等 D．等角的补角相等
4. ∠1 与 ∠2 互余，∠1 = (6x + 8)°，∠2 = (4x－8)°， 则∠1= ，∠2= .
5. 如图，D是直线EF上一点，∠CDE＝90°，∠1＝∠2，哪些角互为余角？哪些角互为补角？
解：∠1与∠ADC，∠1与∠BDC，∠2与∠BDC，∠2与∠ADC互为余角；∠1与∠ADF，∠2与∠ADF，∠2与∠BDE，∠1与∠BDE，∠EDC与∠FDC互为补角．
6.如图，O为直线AB上一点，OD平分∠AOC，∠DOE=90°．（1）∠AOD的余角是______________，∠COD的余角是_______________;（2 ）OE是∠BOC的平分线吗？请说明理由．
解：OE平分∠BOC.理由如下：因为∠DOE=90°，所以∠AOD+∠BOE=90°,∠COD+∠COE=90°，所以∠AOD+∠BOE=∠COD+∠COE.因为OD平分∠AOC，所以∠AOD=∠COD，所以∠COE=∠BOE，所以OE平分∠BOC．
解：因为∠AOC＝∠BOD＝90°，所以∠AOB＋∠BOC＝∠COD＋∠BOC＝90°，所以∠AOB，∠COD都是∠BOC的余角，所以∠AOB＝∠COD.因为∠AOB＝40°，所以∠COD＝40°.