冀教版七年级上册2.7 角的和与差完整版ppt课件

这是一份冀教版七年级上册2.7 角的和与差完整版ppt课件，共18页。PPT课件主要包含了它们的关系有，°24′28″，∠ABC，∠PBC等内容，欢迎下载使用。

1．结合具体图形，明白两个角的和与差的意义，并会进行两个角的和差运算．2．知道角平分线的概念，通过折纸活动进一步明白角平分线的意义．3．体会简单推理．
同学们，我们已经学习了角的有关知识．请问：你们能用手中三角板画出30°、45°、60°、90°的角吗？用三角板怎样做出15°、75°、150 °的角呢？请同学们动手试一试．
你能拼出大于180 °且小于360 °的角吗？（如210 ° ，270 ° ，195 ° ）
你能计算出50 °+20 °吗？89 °15’－32 °10’呢？
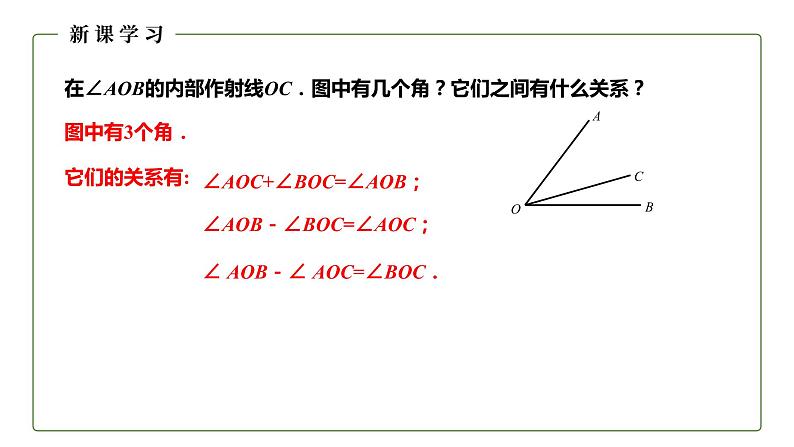
在∠AOB的内部作射线OC．图中有几个角？它们之间有什么关系？
∠AOC+∠BOC=∠AOB；
∠AOB－∠BOC=∠AOC；
∠ AOB－∠ AOC=∠BOC．
一般地，如果一个角的度数是另两个角的度数之和，那么这个角叫做另两个角的和；如果一个角的度数是另两个角的度数之差，那么这个角叫做另两个角的差．
注意：两个角的和与差仍是一个角．
两个角可以相加（或相减），它们的和（或差）也是一个角．它的度数等于这两个角的度数的和（或差）.
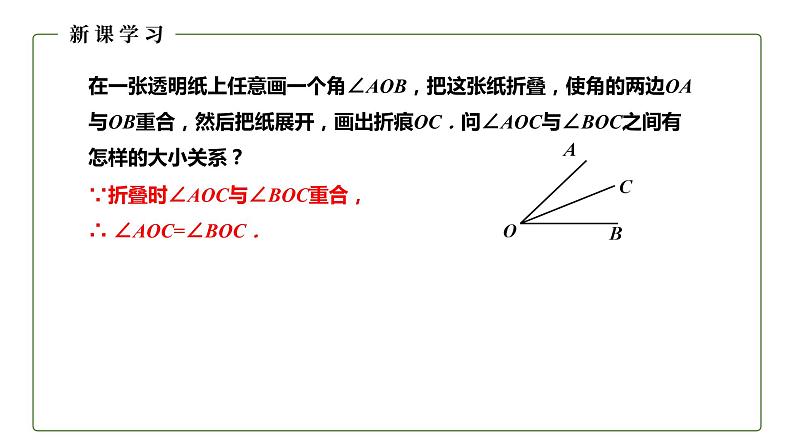
在一张透明纸上任意画一个角∠AOB，把这张纸折叠，使角的两边OA与OB重合，然后把纸展开，画出折痕OC．问∠AOC与∠BOC之间有怎样的大小关系？
∵折叠时∠AOC与∠BOC重合，∴ ∠AOC=∠BOC．
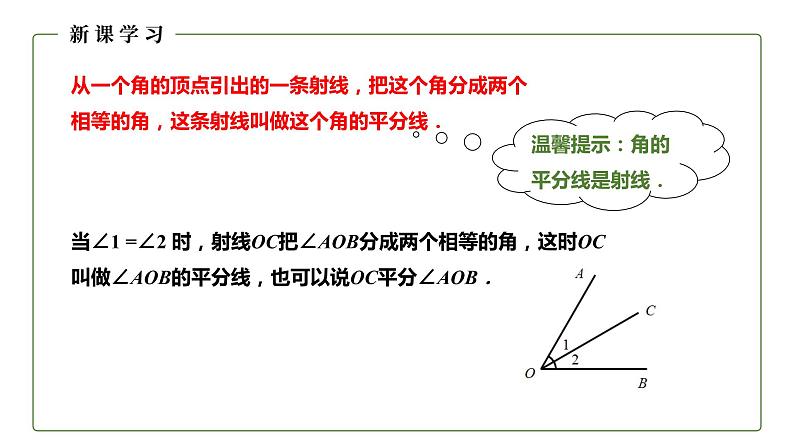
从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线．
当∠1 =∠2 时，射线OC把∠AOB分成两个相等的角，这时OC叫做∠AOB的平分线，也可以说OC平分∠AOB．
温馨提示：角的平分线是射线．
任意画一个角∠AOB，你有什么方法画出它的平分线？
先用量角器量出这个角的大小，再以这个角的顶点为顶点，一边为始边，在角的内部画一条射线，使它与始边所成的角的大小是原角的一半，这条射线就是这个角的平分线．
如图，如果∠AOC=∠DOB，那么∠AOD与∠COB相等吗？说明理由．
相等．因为∠AOC=∠DOB，所以∠AOC+∠COD=∠DOB +∠COD．所以∠AOD=∠COB．
如图，如果∠AOD=∠COB，那么∠AOC与∠DOB相等吗？说明理由．
相等．因为∠AOD=∠COB，所以∠AOD -∠COD=∠COB-∠COD．所以∠AOC=∠DOB．
如图，如果∠AOB=82°，OP是∠AOC的平分线，OQ是∠COB的平分线，请指明∠POQ的度数，并说明理由．
例　已知∠1＝103°24′28″， ∠2＝30°54 ″，求∠1＋∠2和∠1－∠2的度数．
解：∠1＋ ∠2＝ 103°24′28″＋ 30°54 ″．
30° 54 ″
133°24′82 ″
(82 ″=1′22 ″)
所以 ∠1＋∠2=133°25′22″．
∠1－∠2＝ 103°24′28″－30°54 ″．
73°23′34″
(24′28 ″=23′88 ″)
所以 ∠1－∠2= 73°23′24 ″.
1．用一副三角板不能画出（　）A．15° B．135° C．105° D．145°2．如图，OC是∠AOB的平分线，OD是∠AOC的平分线，且∠COD=25°，则∠AOB等于（　）A．50° B．75° C．100° D．120°
3．根据图形填空：（1）∠ABD=∠CBD + ________．（2）∠CBD=∠PBD – ________ =∠ABD – _______．
（3）如图，若∠ABC=90°，∠CBD=20°， 则∠ABD= _____．
（4）在第（3）题的条件下，若BP平分∠ABD， 则∠ABP= ____，∠PBC= _______．
4．如图，∠AOB=120°，∠BOD=90°，OC平分∠BOD，求∠AOC的度数．
解：因为∠BOD=90°，OC平分∠BOD，所以∠BOC=∠DOC=45°，又因为∠AOB=120°，所以∠AOC=∠AOB-∠BOC=120°-45°=75°．
1.两个角可以相加（或相减），它们的和（或差）也是一个角．它的度数等于这两个角的度数的和（或差）.
2.角平分线的定义：从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线．