九年级上册3 正方形的性质与判定图片课件ppt

这是一份九年级上册3 正方形的性质与判定图片课件ppt，共30页。PPT课件主要包含了创设情境导入新课，探究新知经历过程，矩形的中点四边形，菱形的中点四边形，正方形的中点四边形，对角线不垂直不相等，平行四边形，对角线相等，对角线垂直，对角线相等且垂直等内容，欢迎下载使用。
正方形的对角线相等并且互相垂直平分.
有一组邻边相等，并且有一个角是直角的平行四边形，叫做正方形.
正方形的四个角都是直角，四条边相等.
将一张长方形纸对折两次，然后剪下一个角，打开. 怎样剪才能剪出一个正方形？
提示：剪口线与折痕成 45°角即可。
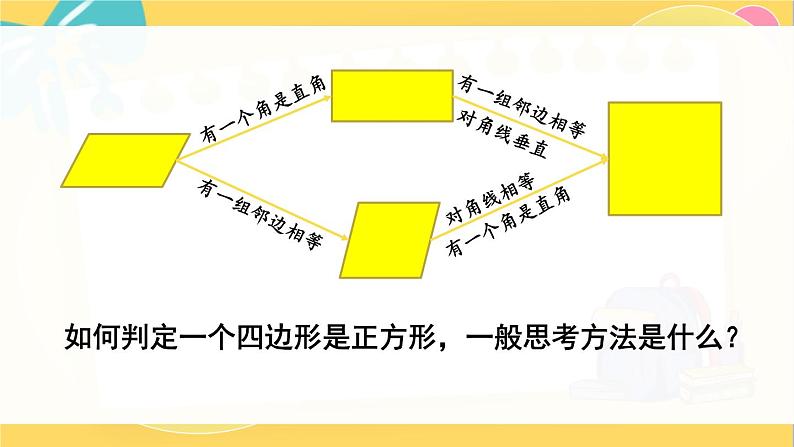
如何判定一个四边形是正方形，一般思考方法是什么？
判断四边形是正方形有哪些方法？
1.先说明它是平行四边形，再说明有一组邻边相等，有一个角是直角.（定义法）
2.先说明它是矩形，再说明这个矩形有一组邻边相等.
3.先说明它是菱形，再说明这个菱形有一个角是直角.
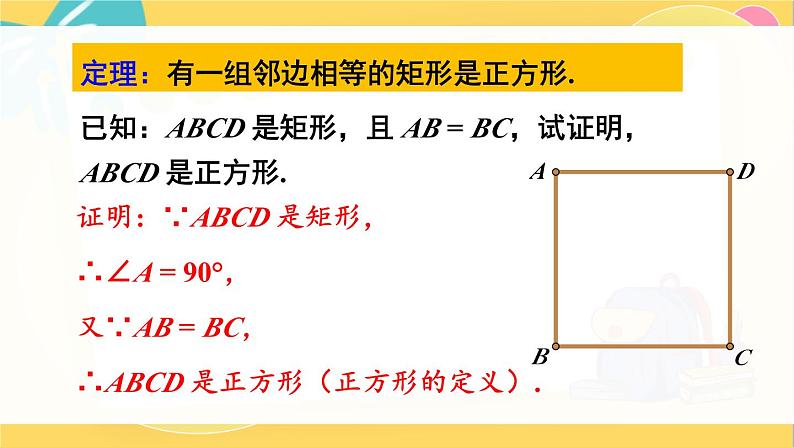
定理：有一组邻边相等的矩形是正方形.
已知：ABCD 是矩形，且 AB = BC，试证明，ABCD 是正方形.
证明：∵ABCD 是矩形，∴∠A = 90°，又∵AB = BC，∴ABCD 是正方形（正方形的定义）.
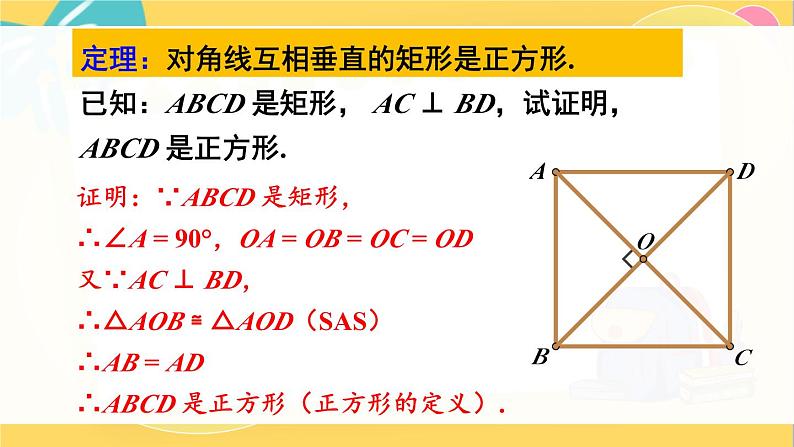
定理：对角线互相垂直的矩形是正方形.
已知：ABCD 是矩形， AC ⊥ BD，试证明，ABCD 是正方形.
证明：∵ABCD 是矩形，∴∠A = 90°，OA = OB = OC = OD又∵AC ⊥ BD，∴△AOB ≌ △AOD（SAS）∴AB = AD∴ABCD 是正方形（正方形的定义）.
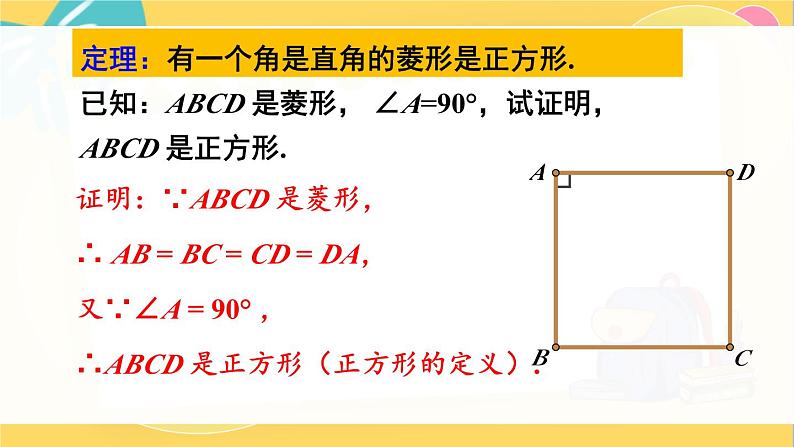
定理：有一个角是直角的菱形是正方形.
已知：ABCD 是菱形， ∠A=90°，试证明，ABCD 是正方形.
证明：∵ABCD 是菱形，∴ AB = BC = CD = DA，又∵∠A = 90° ，∴ABCD 是正方形（正方形的定义）.
定理：对角线相等的菱形是正方形.
已知：ABCD 是菱形， AC = BD，试证明，ABCD 是正方形.
证明：∵ABCD 是菱形，∴ AB = BC = CD = DA，OA = OC = OB = OD∴AC⊥BD（菱形对角线互相垂直）又∵AC = BD ，∴△AOB、△AOD、△BOC、△COD都是等腰直角三角形.∴∠ABC = 90°.∴ABCD 是正方形（正方形的定义）.
例2 已知：如图，在矩形 ABCD 中，BE 平分∠ABC，CE 平分∠DCB，BF∥CE，CF∥BE，求证：四边形 BECF 是正方形.
证明：∵BF∥CE，CF∥BE，∴四边形 BECF 是平行四边形.∵四边形 ABCD 是矩形，∴∠ABC = 90°，∠DCB = 90°.又∵BE平分∠ABC，CE 平分∠DCB，∴∠EBC = ∠ABC = 45°，∠ECB = ∠DCB = 45°.
∴∠EBC = ∠ECB. ∴ EB = EC.∴□ BECF 是菱形（菱形的定义）.在△EBC 中，∵∠EBC = 45°，∠ECB = 45°，∴∠BEC = 90°.∴菱形 BECF 是正方形（有一个角是直角的菱形是正方形）.
三角形的中位线平行于第三边并且等于它的一半．
如图，在△ABC 中，EF 为 △ABC 的中位线，①若∠BEF = 30°，则∠A =______. ②若 EF = 8 cm, 则 AC =______.
你还记得三角形的中位线定理吗？
一般四边形的中点四边形
如图，任意画一个四边形，以四边的中点为顶点组成一个新四边形，这个新四边形的形状有什么特征？
任意四边形的中点四边形 是平行四边形.
如果四边形 ABCD 变为特殊的四边形，中点四边形 EFGH 会有怎样的变化呢？
平行四边形的中点四边形
平行四边形的中点四边形会是什么形状？
平行四边形的中点四边形是平行四边形.
你能试着证明这个结论吗？（提示：连接AC、BD）
矩形的中点四边形会是什么形状？
矩形的中点四边形是菱形.
你能试着证明这个结论吗？
已知：如图，点 E，F，G，H 分别是矩形 ABCD 各边的中点. 求证：四边形 EFGH 为菱形.
证明：连接 AC，BD，∵ E，F 分别是 AB 和 BC 边中点，∴EF∥AC 且 EF = AC，同理可证 HG∥AC且HG = AC，EH∥BD且EH= BD，FG∥BD且FG= BD.∴四边形 EFGH 为平行四边形.又∵四边形 ABCD 是矩形∴AC=BD（矩形的对角线相等），∴EF = EH∴四边形 EFGH 是菱形（菱形的定义）
菱形的中点四边形会是什么形状？
菱形的中点四边形是矩形.
已知：如图，点 E，F，G，H 分别是菱形 ABCD 各边的中点. 求证：四边形 EFGH 为矩形.
证明：连接 AC，BD，∵ E，F 分别是 AB 和 BC 边中点，∴ EF∥AC ，同理可证 HG∥AC，EH∥BD，FG∥BD.∴EF∥HG，EH∥FG，∴四边形 EFGH ，PFQO 为平行四边形.又∵四边形 ABCD 是菱形∴AC⊥BD（菱形的对角线互相垂直），∴∠1 = 90°，∠2=90°.∴四边形 EFGH 是矩形（矩形的定义）
正方形的中点四边形会是什么形状？
已知：如图，点 E，F，G，H 分别是正方形 ABCD 各边的中点. 求证：四边形 EFGH 为正方形.
证明：连接 AC，BD，∵ E，F 分别是 AB 和 BC 边中点，∴ EF∥AC 且EF = AC，同理可证 HG∥AC 且 HG = AC，EH∥BD且 EH = BD，FG∥BD且FG = BD.∴四边形 PFQO 为平行四边形.
又∵四边形 ABCD 是正方形，∴AC = BD（正方形的对角线相等） AC⊥BD（正方形的对角线互相垂直），∴EF = FG = HG = EH，∠1 = 90°.∴四边形 EFGH 是菱形（四边相等的四边形是菱形），∠2 = 90°.∴四边形 EFGH 为正方形（有一个角是直角的菱形是正方形）.
思考：决定中点四边形形状的关键因素是什么？
决定中点四边形 EFGH 的形状的主要因素是原四边形 ABCD 的对角线的长度和位置关系。
已知：如图，E，F 是正方形 ABCD 的对角线 BD 上的两点，且 BE = DF. 求证：四边形 AECF 是菱形.
【选自教材P25 习题1.8 第2题】
证明: 在正方形 ABCD 中,BE ＝DF,易证△CEB≌△AEB≌△AFD≌△CFD ,即 CE ＝AE ＝AF ＝FC,∴四边形 AECF 是菱形．
2. 如图，在正方形 ABCD 中，E，F，G，H 分别在它的 四条边上，且 AE = BF = CG = DH. 四边形 EFGH 是 什么特殊四边形？你是如何判断的？
解：四边形 EFGH 是正方形.∵在正方形 ABCD 中，AE=BF=CG=DH，易证 △AEH≌△DHG≌△CGF≌△BFE,即EH ＝HG＝GF＝FE,且∠AHE＝∠DGH ．∵∠DGH ＋∠DHG＝90°,∴∠EHG＝180°－(∠AHE＋∠DHG)＝90°,∴四边形 EFGH 是正方形
【选自教材P25 习题1.8 第3题】
3. 如图，正方形 ABCD 的对角线相交于点 O，正方形A′B′C′O 与正方形 ABCD 的边长相等. 在正方形A′B′C′O绕点 O 旋转 的过程中，两个正方形重叠的部分与正方形ABCD 的面积 有什么关系？请证明你的结论.
【选自教材P25 习题1.8 第4题】
S重叠部分 = S正方形ABCD
证明:如图,正方形 OA′B′C′ 分别交 AB、BC 于点 E、F．∵OC ＝ OB,∠C′OA′＝∠COB ＝ 90°,∠OCB ＝∠OBA ＝ 45°,∴ ∠COF ＝ ∠BOE,则△OFC ≌ △OEB．∴S重叠部分＝ S△OEB+ S△OBF = S△OFC + S△OBF = S△OBC = S正方形ABCD .
这节课你们都学会了哪些知识？