



初中数学24.2直角三角形的性质授课课件ppt
展开第24章 解直角三角形
24.2 直角三角形的性质
知识点1 直角三角形斜边上的中线的性质
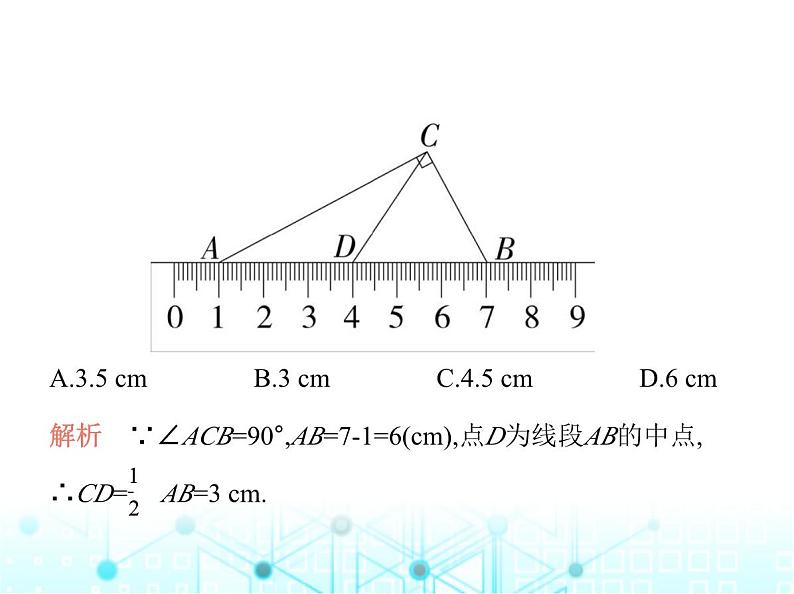
1.(2023湖南株洲中考)一技术人员用刻度尺(单位:cm)测量某 三角形部件的尺寸.如图所示,已知∠ACB=90°,点D为边AB的 中点,点A、B对应的刻度为1、7,则CD= ( )
A.3.5 cm B.3 cm C.4.5 cm D.6 cm
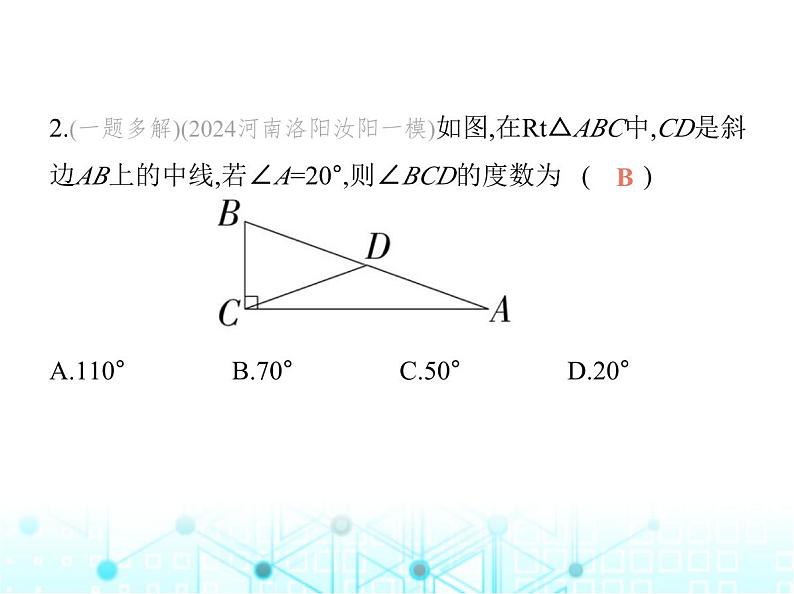
2.(一题多解)(2024河南洛阳汝阳一模)如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A=20°,则∠BCD的度数为 ( ) A.110° B.70° C.50° D.20°
解析 解法1(利用直角):在Rt△ABC中,CD是斜边AB上的中 线,∴CD=DA,∵∠A=20°,∴∠DCA=∠A=20°,∴∠BCD=90°- ∠DCA=90°-20°=70°.解法2(利用三角形内角和):在Rt△ABC中,∠ACB=90°,∠A=2 0°,∴∠B=70°.∵CD是斜边AB上的中线,∴BD=CD,∴∠BCD =∠B=70°.
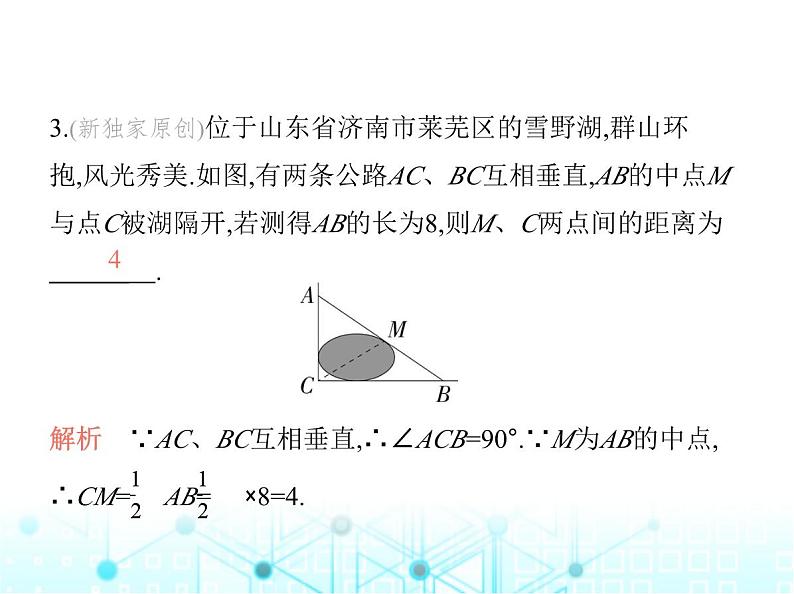
3.(新独家原创)位于山东省济南市莱芜区的雪野湖,群山环 抱,风光秀美.如图,有两条公路AC、BC互相垂直,AB的中点M 与点C被湖隔开,若测得AB的长为8,则M、C两点间的距离为 .
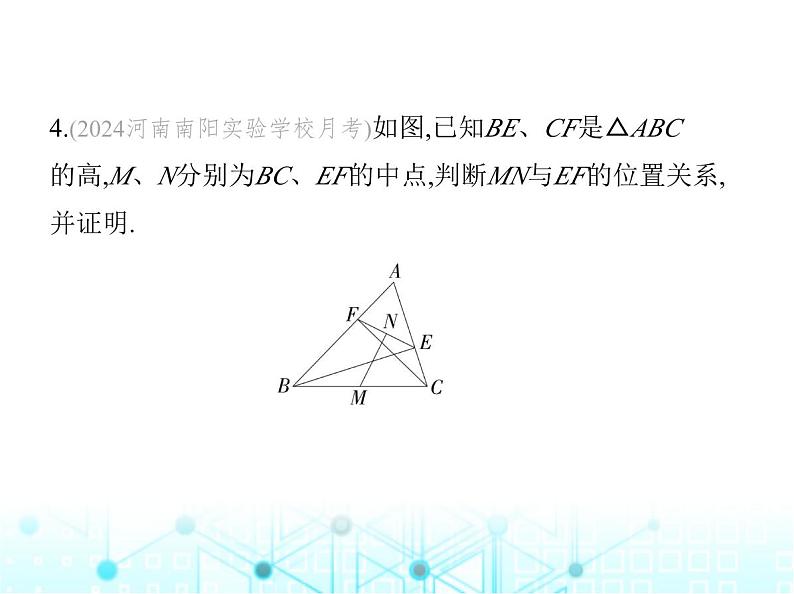
4.(2024河南南阳实验学校月考)如图,已知BE、CF是△ABC 的高,M、N分别为BC、EF的中点,判断MN与EF的位置关系, 并证明.
解析 MN⊥EF.证明:如图,连结ME,MF.∵CF是AB边的高,∴ CF⊥AB,∴∠BFC=90°.∵点M是BC的中点,∴MF= BC,同理,ME= BC,∴ME=MF.∵点N为EF的中点,∴MN⊥EF.
知识点2 含30°角的直角三角形的性质
5.(新独家原创)(情境题·革命文化)“重温红色记忆,传承红色 基因”,某中学的学生参加红色研学活动,爬山体验长征精 神.如图所示的是下山时所用的一段索道的示意图,已知A、 B两点间的距离为30 m,∠BAC=30°,则缆车从B点到达A点的 过程中,下降的高度(BC的长)为( )
A.10 m B.15 m C.20 m D.30 m
6.(2023贵州中考)2023年5月26日,“2023中国国际大数据产 业博览会”在贵阳开幕,在“自动化立体库”中有许多几何 元素,其中有一个等腰三角形模型(示意图如图所示),它的顶 角为120°,腰长为12 m,则底边上的高是( ) A.4 m B.6 m C.10 m D.12 m
解析 作AD⊥BC于点D(图略),在△ABC中,∠BAC=120°,AB =AC,∴∠B=∠C= ×(180°-∠BAC)=30°,∵AD⊥BC,∴AD= AB= ×12=6(m),故底边上的高为6 m.
7.(易错题)(2024河南鹤壁淇滨期末)含30°角的直角三角板与 直线l1,l2的位置关系如图所示,已知l1∥l2,∠A=30°,∠1=60°,若 AB=6,则CD的长为 .
解析 ∵∠A=30°,∴∠DBC=90°-∠A=60°,∵l1∥l2,∴∠BDC=∠1=60°,∴△BDC为等边三角形,∴CD=BC,∵AB=6,∴BC= AB=3,∴CD=3.
8.(教材变式·P104练习T2)(2024山西晋城二中月考)一艘轮船 自西向东航行,在A处测得小岛P在北偏东75°方向,航行7海 里后,在B处测得小岛P在北偏东60°方向,若小岛周围3.8海里 内有暗礁,问该船一直向东航行,有无触礁的危险?并说明原 因.
解析 有触礁危险.理由:如图,作PD⊥AB于D,∵在A处测得 小岛P在北偏东75°方向,∴∠PAB=15°,∵在B处测得小岛P在 北偏东60°方向,∴∠PBD=30°,∴∠APB=∠PAB=15°,∴PB= AB=7海里,∴PD= PB=3.5海里,∵3.5<3.8,∴该船继续向东航行,有触礁的危险.
9.(一题多解)(教材变式·P122T14)(2024湖南衡阳常宁二模,7, ★★☆)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,CD⊥ AB于点D,E是AB的中点,则DE的长为 ( ) A.1 B.2 C.3 D.4
解析 解法1(利用含30°角的直角三角形的性质):∵AB=4,E 是AB的中点,∴CE= AB= ×4=2,CE=AE,∴∠ACE=∠A=30°,∴∠CED=30°+30°=60°.∵CD⊥AB,∴∠CDE=90°,∴∠DCE=30°,∴DE= CE= ×2=1.解法2(利用等边三角形的“三线合一”):∵∠ACB=90°,∠A=30°,∴∠B=60°,∵E是AB的中点,AB=4,∴CE=BE= AB= ×4=2,∴△BCE为等边三角形,∵CD⊥AB,∴DE=BD= BE= ×2=1.
10.(2023内蒙古赤峰中考,8,★★★)如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,点F是AB中点,连结CF,把线段CF沿射线BC方向平移到DE,点D在AC上.则线段CF在平移过程中 扫过区域形成的四边形CFDE的周长和面积分别是 ( ) A.16,6 B.18,18 C.16,12 D.12,16
解析 由平移的性质可知DF∥CE,DF=CE,∴四边形CFDE 是平行四边形,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,∴AC = = =8,在Rt△ABC中,∠ACB=90°,AB=10,点F是AB的中点,∴CF= AB=5,∵DF∥CE,点F是AB的中点,∴ = = ,∠CDF=180°-∠ABC=90°,∴点D是AC的中点,
∴CD= AC=4,∵点F是AB的中点,点D是AC的中点,∴DF是Rt△ABC的中位线,∴DF= BC=3,∴四边形CFDE的周长为2
(DF+CF)=2×(3+5)=16,四边形CFDE的面积为DF·CD=3×4=12.
11.(新考法)(2024山西临汾襄汾二模,17,★★☆)图1是一种矩 形时钟,图2是时钟示意图,时钟数字2的刻度在矩形ABCD的 对角线BD上,时钟中心在矩形ABCD对角线的交点O上.若AB =1,则BC的长为 (结果保留根号).
解析 根据钟表中刻度的划分挖掘出30°角是本题的求解关 键,设计新颖.如图,过点O作OE⊥CD,垂足为E.由钟表上的刻 度划分可知,每经过1小时,时针转过的角度为30°,∴∠DOE= 30°.在矩形ABCD中,∠C=90°,CD=AB=1,OE∥BC,∴∠DBC= ∠DOE=30°,∴BD=2CD=2,∴BC= = .
12.(动点问题)(2024福建泉州洛江二模,23,★★☆)如图,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0
解析 (1)证明:∵在Rt△ABC中,∠B=90°,∠A=60°,∴∠C=90°-∠A=30°.在Rt△CDF中,∠C=30°,CD=4t cm,∴DF= CD=2t cm,∵点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速 运动,∴AE=2t cm,∴AE=DF.(2)分情况求解如下:①当∠DEF=90°时,由(1)易知四边形AEFD为平行四边形,∴ EF∥AD,∴∠ADE=∠DEF=90°,∵∠A=60°,∴∠AED=30°,∴ AD= AE=t cm,∵AD=(60-4t)cm,∴60-4t=t,解得t=12;
②当∠EDF=90°时,四边形EBFD为矩形,在Rt△AED中,∠A= 60°,则∠ADE=30°,∴AD=2AE=4t cm,∴60-4t=4t,解得t= .③不存在∠EFD=90°的情况.综上所述,当t= 或12时,△DEF为直角三角形.
13.(推理能力)(2024四川眉山二模)如图1,BD是Rt△ABC斜边 AC上的中线.(1)求证:BD= AC;(2)如图2,AB=6,BC=8,点P是BC上一个不与B、C重合的动点, 过点P分别作AC、BD的垂线,垂足分别为E、F.当P在BC上 移动时,求PE+PF的值.
图1 图2
解析 (1)证明:如图1,过点A作AE∥BC,交BD的延长线于 点E,连结CE,∴∠DAE=∠BCD,∵BD是Rt△ABC斜边上的中 线,∴AD=CD,∵∠ADE=∠BDC,∴△ADE≌△CDB,∴DE= BD,∴四边形ABCE是平行四边形,∴BD=DE= BE,∵∠ABC=90°,∴四边形ABCE是矩形,∴AC=BE,∴BD= AC. 图1 图2
华师大版九年级上册24.2直角三角形的性质课文ppt课件: 这是一份华师大版九年级上册24.2直角三角形的性质课文ppt课件,共16页。PPT课件主要包含了学习目标,知识回顾,提出猜想,归纳结论,课堂小结等内容,欢迎下载使用。
初中数学华师大版九年级上册24.2直角三角形的性质教课内容课件ppt: 这是一份初中数学华师大版九年级上册24.2直角三角形的性质教课内容课件ppt,共21页。PPT课件主要包含了复习回顾,角的关系,边的关系,实验探究探索新知,归纳定理,假命题,含30°直角三角形,迁移新知能力拓展,巩固提高尝试反馈,化斜为直等内容,欢迎下载使用。
初中数学华师大版九年级上册24.2直角三角形的性质教课内容ppt课件: 这是一份初中数学华师大版九年级上册24.2直角三角形的性质教课内容ppt课件,共18页。PPT课件主要包含了知道怎样剪了吗,直角三角形的性质,变一变,试一试,再变一变,今天我学会了,基本图形,课外思考等内容,欢迎下载使用。














