





冀教版25.4 相似三角形的判定备课ppt课件
展开1.理解“两边对应成比例且夹角相等的两个三角形相似”的判定定理及证明过程,能运用该定理证明三角形相似;2.类比全等三角形判定引出猜想,从不断变化的图形中,体会从特殊到一般的研究方法,在证明定理过程中,渗透转化思想,进一步积累研究图形问题的经验;3.感悟数学知识之间的内在联系,提升探究问题的兴趣,激发数学学习热情.
判断两个三角形相似,你有哪些方法?
方法1:通过定义(不常用)
利用刻度尺和量角器画△ABC与△A′B′C′,使∠A=∠A′, =2. (1)比较∠C′与∠C(或∠B′与∠B)的大小.(2)由比较的结果,能断定△ ABC和△A′B′C′相似吗?(3)改变对应边的比值和夹角的度数(但保持夹角相等),再画出两个三角形,它们相似吗?
如果两个三角形的两组对应边成比例,并且相应的夹角相等,那么这两个三角形相似. 即若∠A=∠A′, =k ,则△ABC∽ △A′B′C′. 你能给出证明吗?
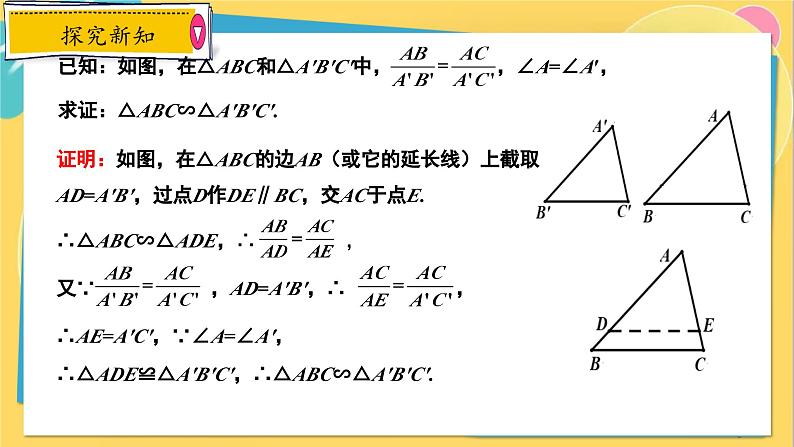
已知:如图,在△ABC和△A′B′C′中, ,∠A=∠A′,求证:△ABC∽△A′B′C′.
证明:如图,在△ABC的边AB(或它的延长线)上截取AD=A′B′,过点D作DE∥BC,交AC于点E.∴△ABC∽△ADE,∴ ,又∵ ,AD=A′B′,∴ ,∴AE=A′C′,∵∠A=∠A′,∴△ADE≌△A′B′C′,∴△ABC∽△A′B′C′.
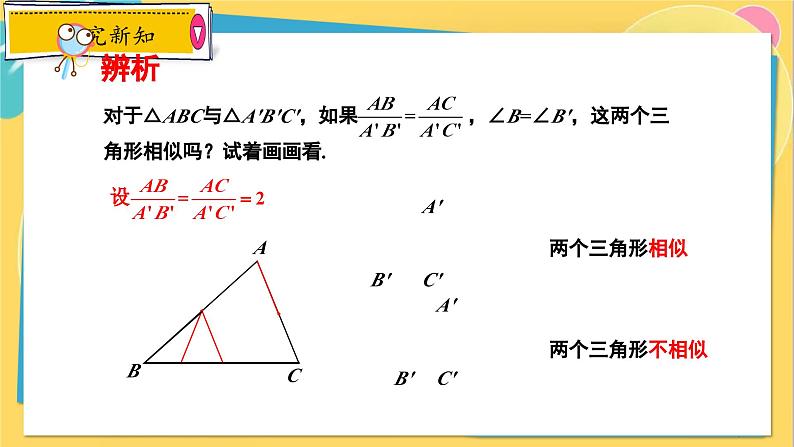
对于△ABC与△A′B′C′,如果 ,∠B=∠B′,这两个三角形相似吗?试着画画看.
两边对应成比例且夹角相等的两个三角形相似.
特别提醒: 运用该定理判定相似时,一定要注意边角的关系,相等的角一定是成比例的两组对应边的夹角. 类似于判定三角形全等的SAS 的方法.
相似三角形的判定定理2
几何语言:∵ ,∠A=∠A′,∴△ABC∽△A′B′C′.
已知:在△ABC与△A′B′C′中,∠A=∠A′=60°, AB=4 cm,AC=8 cm,A′B′=11 cm,A′C′=22 cm. 求证:△ABC∽△A′B′C′.
又∵ ∠A=∠A′=60°,∴△ABC∽△A′B′C′.
利用三角形两边成比例且夹角相等证两三角形相似的方法:1.首先找出两个三角形中相等的那个角;2.再分别找出两个三角形中夹这个角的两条边,并按大小排列找出对应边;3.最后看这两组对应边是否成比例,若成比例则两个三角形相似,否则不相似.
如图,在△ABC中,CD∥EF,AF=1,AD=3,AE=2.(1)求AC的长;(2)若AB=9,求证:△ABC∽△ADE.
解:(1)∵CD∥EF, ∴ ,∵AF=1,AD=3,AE=2,∴ ,∴AC=6; (2)证明:∵AD=3,AB=9,AE=2,AC=6,∴ ,∵∠DAE=∠BAC,∴△ABC∽△ADE.
如图,在△ABC中,AB=16,AC=8,在AC上取一点D,使AD=3,如果在AB上取点E,使△ADE和△ABC相似,求AE的长.
点拨:已知有一对角相等,要使这两个三角形相似,夹这对角的两边对应成比例.但两边的对应关系无法确定,所以应分两种情况考虑.
解:设AE的长为x.∠A是公共角,要使△ADE和△ABC相似,则有即 解得x=6或x=1.5.所以AE的长为6或1.5.
要使两个三角形相似,若已知有一对角相等,则需夹这对角的两边对应成比例.当无法确定对应关系时,则夹这对角的两边的比就有两种情况的可能,因此必须进行分类讨论;否则就会因漏解而致错.
冀教版九年级上册25.4 相似三角形的判定教学ppt课件: 这是一份冀教版九年级上册<a href="/sx/tb_c107212_t3/?tag_id=26" target="_blank">25.4 相似三角形的判定教学ppt课件</a>,共24页。PPT课件主要包含了知识回顾,知识点,直角三角形相似的条件,答案C等内容,欢迎下载使用。
初中数学冀教版九年级上册第25章 图形的相似25.4 相似三角形的判定图文ppt课件: 这是一份初中数学冀教版九年级上册<a href="/sx/tb_c107212_t3/?tag_id=26" target="_blank">第25章 图形的相似25.4 相似三角形的判定图文ppt课件</a>,共18页。PPT课件主要包含了如图已知∠α∠β,由SAS可证得全等,知识点,或45等内容,欢迎下载使用。
初中数学华师大版九年级上册2. 相似三角形的判定课文配套课件ppt: 这是一份初中数学华师大版九年级上册<a href="/sx/tb_c21348_t3/?tag_id=26" target="_blank">2. 相似三角形的判定课文配套课件ppt</a>,共15页。PPT课件主要包含了相似三角形,知识要点1,相似三角形的判定2,符号语言,知识要点2,相似三角形的判定3,相似三角形判定,判定1,判定3,三边对应成比例等内容,欢迎下载使用。













